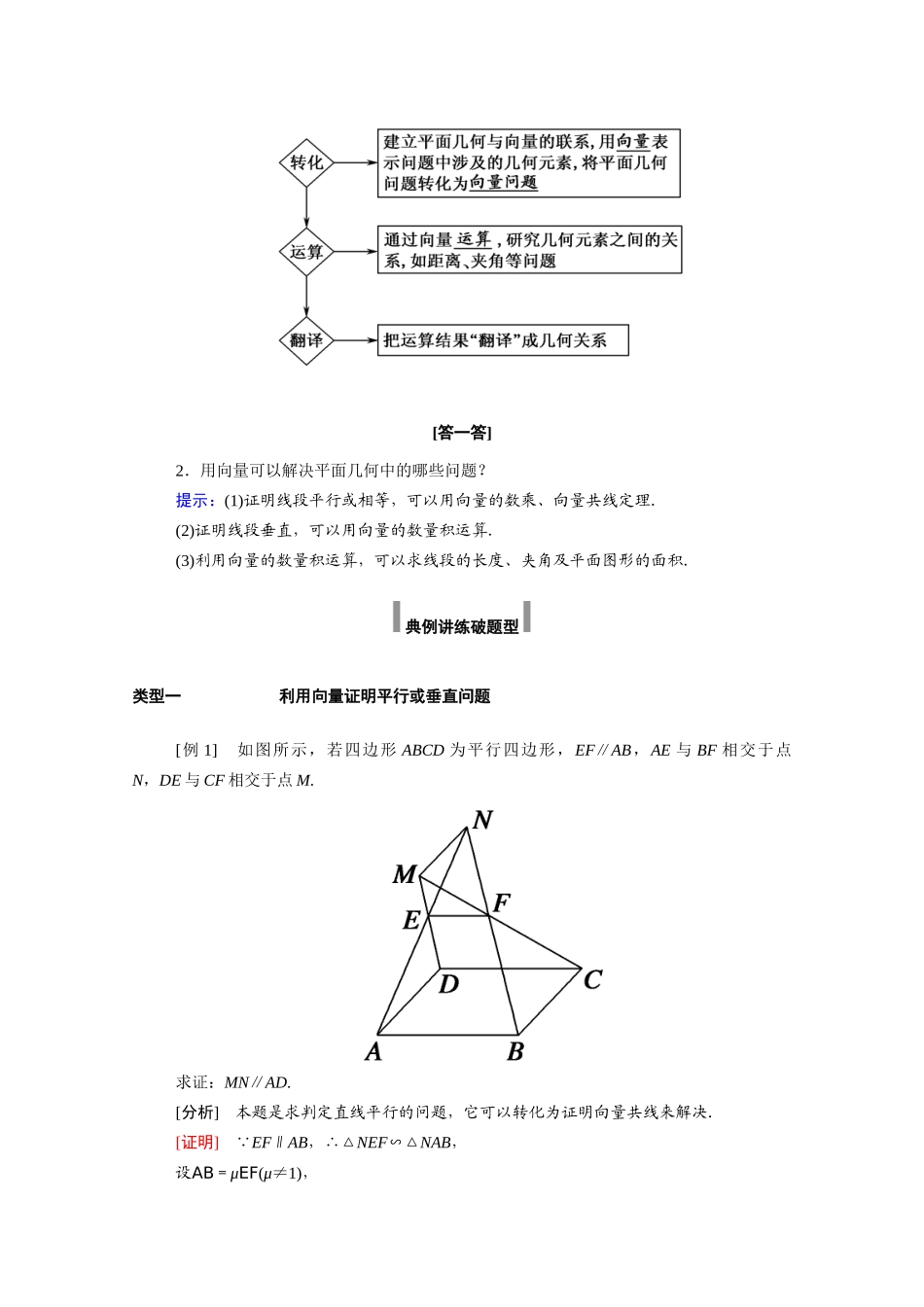
6.4 平面向量的应用6.4.1 平面几何中的向量方法[目标] 1.通过平行四边形这个几何模型,归纳总结出用向量方法解决平面几何的问题的“三步曲”;2.明确平面几何图形中的有关性质,如平移、全等、相似、长度、夹角等可以由向量的线性运算及数量积表示.[重点] 用向量方法解决实际问题的基本方法:向量法解决几何问题的“三步曲”.[难点] 如何将几何等实际问题化归为向量问题. 要点整合夯基础 知识点一 向量方法在几何中的应用[填一填]对于平面向量 a=(x1,y1),b=(x2,y2).(1)证明线段平行问题,包括相似问题,常用向量平行(共线)的等价条件:a∥b(b≠0)⇔b = λ a ⇔x1y2- x 2y1= 0 .(2)证明垂直问题,如证明四边形是矩形、正方形等,常用向量垂直的等价条件:非零向量 a,b,a⊥b⇔a · b = 0 ⇔x1x2+ y 1y2= 0 .(3)求夹角问题,往往利用向量的夹角公式 cosθ==.(4)求线段的长度或证明线段相等,可以利用向量的线性运算、向量模的公式:|a|=或=.[答一答]1.已知 A(x1,y1),B(x2,y2),a=AB,如何用坐标表示 a 和|a|?提示:a=(x2-x1,y2-y1),|a|=.知识点二 平面几何中的向量方法[填一填]用向量方法解决平面几何问题的“三步曲”.[答一答]2.用向量可以解决平面几何中的哪些问题?提示:(1)证明线段平行或相等,可以用向量的数乘、向量共线定理.(2)证明线段垂直,可以用向量的数量积运算.(3)利用向量的数量积运算,可以求线段的长度、夹角及平面图形的面积. 典例讲练破题型 类型一 利用向量证明平行或垂直问题[例 1] 如图所示,若四边形 ABCD 为平行四边形,EF∥AB,AE 与 BF 相交于点N,DE 与 CF 相交于点 M.求证:MN∥AD.[分析] 本题是求判定直线平行的问题,它可以转化为证明向量共线来解决.[证明] EF∥AB,∴△NEF∽△NAB,设AB=μEF(μ≠1),则=μ,AE=(μ-1)EN,同理,由EF∥CD,可得DE=(μ-1)EM,∴AD=ED-EA=AE-DE=(μ-1)MN, μ≠1,令 λ=μ-1,∴AD=λMN,即 AD∥MN.[变式训练 1] 如图所示,四边形 ABCD 是菱形,AC 和 BD 是它的两条对角线,试用向量证明:AC⊥BD.证明: AC=AB+AD,BD=AD-AB,∴AC·BD=(AB+AD)·(AD-AB)=|AD|2-|AB|2=0.∴AC⊥BD,∴AC⊥BD.类型二 利用向量解决长度和夹角问题 [例 2] 如图,在△ABC 中,∠BAC=120°,AB=AC=3,点 D 在线段 BC 上,且 BD=DC.求:(1)AD 的长;(2)∠DAC ...