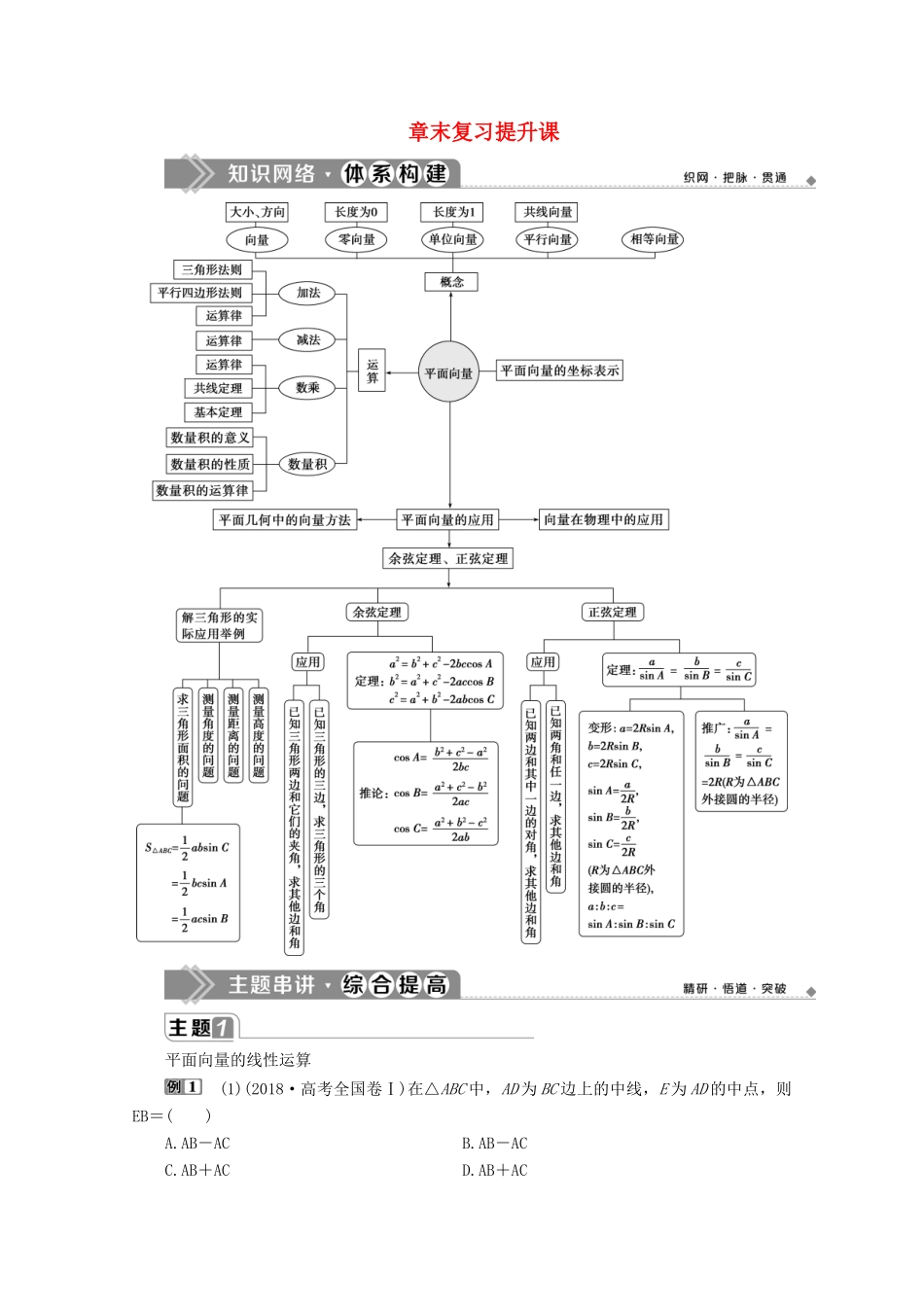
章末复习提升课平面向量的线性运算 (1)(2018·高考全国卷Ⅰ)在△ABC 中,AD 为 BC 边上的中线,E 为 AD 的中点,则EB=( )A.AB-AC B.AB-ACC.AB+AC D.AB+AC(2)如图所示,在正方形 ABCD 中,M 是 BC 的中点,若AC=λAM+μBD,则 λ+μ=( )A. B.C. D.2【解析】 (1)法一:如图所示,EB=ED+DB=AD+CB=×(AB+AC)+(AB-AC)=AB-AC,故选 A.法二:EB=AB-AE=AB-AD=AB-×(AB+AC)=AB-AC,故选 A.(2)因为AC=λAM+μBD=λ(AB+BM)+μ(BA+AD)=λ(AB+AD)+μ(-AB+AD)=(λ-μ)+AD,且AC=AB+AD,所以得所以 λ+μ=,故选 B.【答案】 (1)A (2)B向量线性运算的基本原则向量的加法、减法和数乘运算统称为向量的线性运算,向量的线性运算的结果仍是一个向量,因此,对它们的运算法则、运算律的理解和运用要注意向量的大小和方向两个方面. 已知平面向量 a=(2,-1),b=(1,1),c=(-5,1).若(a+kb)∥c,则实数 k 的值为( )A.2 B.C. D.-解析:选 B.由题意知,a+kb=(2,-1)+k(1,1)=(k+2,k-1),由(a+kb)∥c,得-5(k-1)=k+2,解得 k=,故选 B.平面向量数量积的运算 如 图 , 在 平 面 四 边 形 ABCD 中 , AB⊥BC , AD⊥CD , ∠ BAD =120°,AB=AD=1.若点 E 为边 CD 上的动点,则AE·BE的最小值为( )A. B.C. D.3【解析】 以 A 为坐标原点,AB 所在直线为 x 轴,建立如图的平面直角坐标系,因为在平面四边形 ABCD 中,AB=AD=1,∠BAD=120° , 所 以A(0,0),B(1,0),D,设 C(1,m),E(x,y),所以DC=,AD=,因为 AD⊥CD,所以·=0,即×+=0,解得 m=,即C(1,),因为 E在 CD 上,所以≤y≤,由CE∥DC,得(x-1)=(y-),即 x=y-2,因为AE=(x,y),BE=(x-1,y),所以AE·BE=(x,y)·(x-1,y)=x2-x+y2=(y-2)2-y+2+y2=4y2-5y+6,令 f(y)=4y2-5y+6,y∈.因为函数 f(y)=4y2-5y+6 在上单调递减,在上单调递增,所以f(y)min=4×-5×+6=.所以AE·BE的最小值为,故选 A.【答案】 A向量数量积的两种计算方法(1)当已知向量的模和夹角 θ 时,可利用定义法求解,即 a·b=|a||b|cos θ.(2)当已知向量的坐标时,可利用坐标法求解,即若 a=(x1,y1),b=(x2,y2),则 a·b=x1x2+y1y2. 1.已知向量 a,b 的夹角为,|a|=,|b|=2,则 a·(a-2b)=________.解析:a·(...