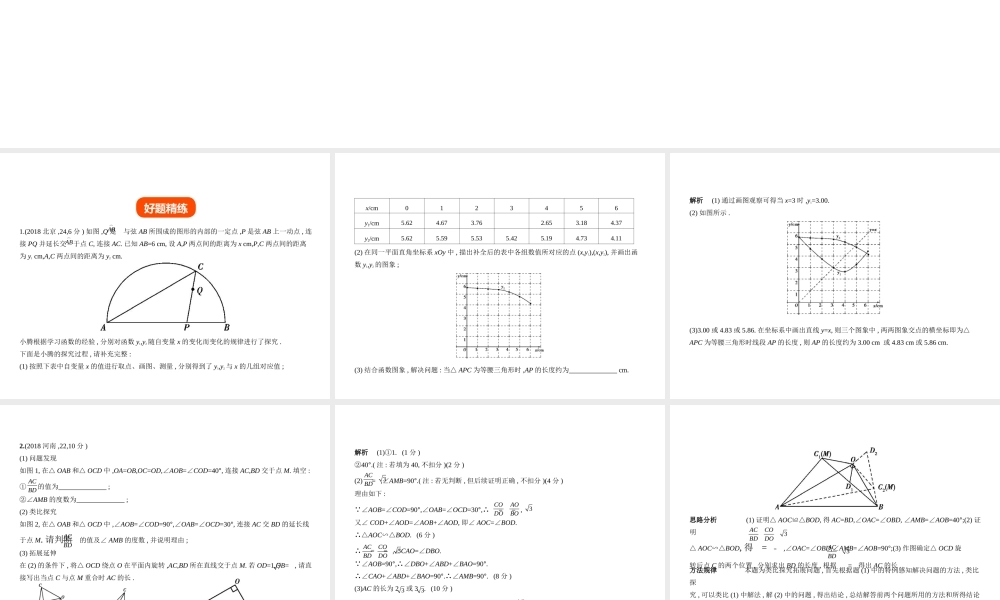
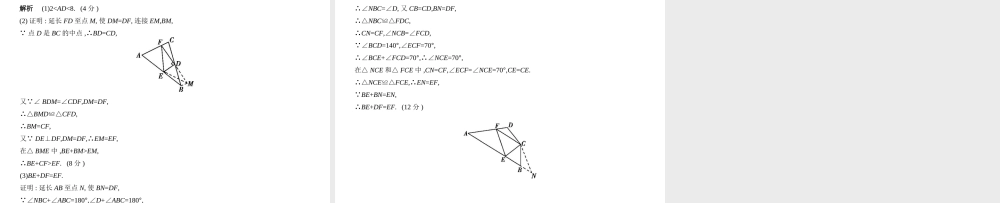
§8.3 实验操作型中考数学 ( 山东专用 )1.(2018 北京 ,24,6 分 ) 如图 ,Q 是 与弦 AB 所围成的图形的内部的一定点 ,P 是弦 AB 上一动点 , 连接 PQ 并延长交 于点 C, 连接 AC. 已知 AB=6 cm, 设 A,P 两点间的距离为 x cm,P,C 两点间的距离为 y1 cm,A,C 两点间的距离为 y2 cm. 小腾根据学习函数的经验 , 分别对函数 y1,y2 随自变量 x 的变化而变化的规律进行了探究 .下面是小腾的探究过程 , 请补充完整 :(1) 按照下表中自变量 x 的值进行取点、画图、测量 , 分别得到了 y1,y2 与 x 的几组对应值 ;AB︵AB︵好题精练x/cm0123456y1/cm5.624.673.76 2.653.184.37y2/cm5.625.595.535.425.194.734.11(2) 在同一平面直角坐标系 xOy 中 , 描出补全后的表中各组数值所对应的点 (x,y1),(x,y2), 并画出函数 y1,y2 的图象 ;(3) 结合函数图象 , 解决问题 : 当△ APC 为等腰三角形时 ,AP 的长度约为 cm.解析 (1) 通过画图观察可得当 x=3 时 ,y1=3.00.(2) 如图所示 . (3)3.00 或 4.83 或 5.86. 在坐标系中画出直线 y=x, 则三个图象中 , 两两图象交点的横坐标即为△APC 为等腰三角形时线段 AP 的长度 , 则 AP 的长度约为 3.00 cm 或 4.83 cm 或 5.86 cm.2.(2018 河南 ,22,10 分 )(1) 问题发现如图 1, 在△ OAB 和△ OCD 中 ,OA=OB,OC=OD,∠AOB=∠COD=40°, 连接 AC,BD 交于点 M. 填空 :① 的值为 ;②∠AMB 的度数为 ;(2) 类比探究如图 2, 在△ OAB 和△ OCD 中 ,∠AOB=∠COD=90°,∠OAB=∠OCD=30°, 连接 AC 交 BD 的延长线于点 M. 请判断 的值及∠ AMB 的度数 , 并说明理由 ;(3) 拓展延伸在 (2) 的条件下 , 将△ OCD 绕点 O 在平面内旋转 ,AC,BD 所在直线交于点 M. 若 OD=1,OB= , 请直接写出当点 C 与点 M 重合时 AC 的长 .ACBDACBD7解析 (1)1.① (1 分 )②40°.( 注 : 若填为 40, 不扣分 )(2 分 )(2) = ,∠AMB=90°.( 注 : 若无判断 , 但后续证明正确 , 不扣分 )(4 分 )理由如下 : ∠AOB=∠COD=90°,∠OAB=∠OCD=30°,∴ = = ,又∠ COD+∠AOD=∠AOB+∠AOD, 即∠ AOC=∠BOD.∴△AOC∽△BOD. (6 分 )∴ = = ,∠CAO=∠DBO. ∠AOB=90°,∴∠DBO+∠ABD+∠BAO=90°.∴∠CAO+∠ABD+∠BAO=90°.∴∠AMB=90°. (8 分 )(3)AC 的长为 2...