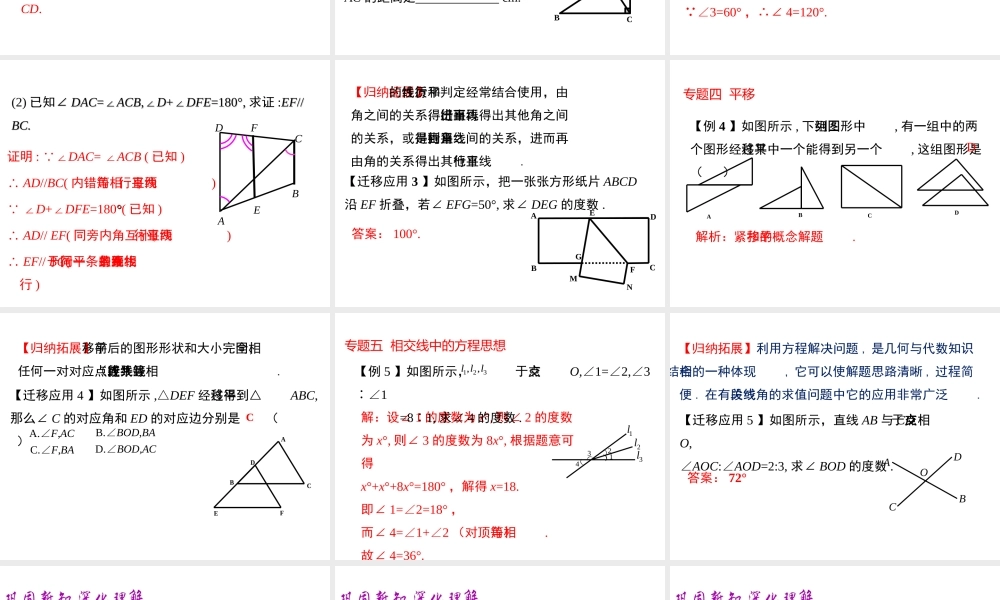
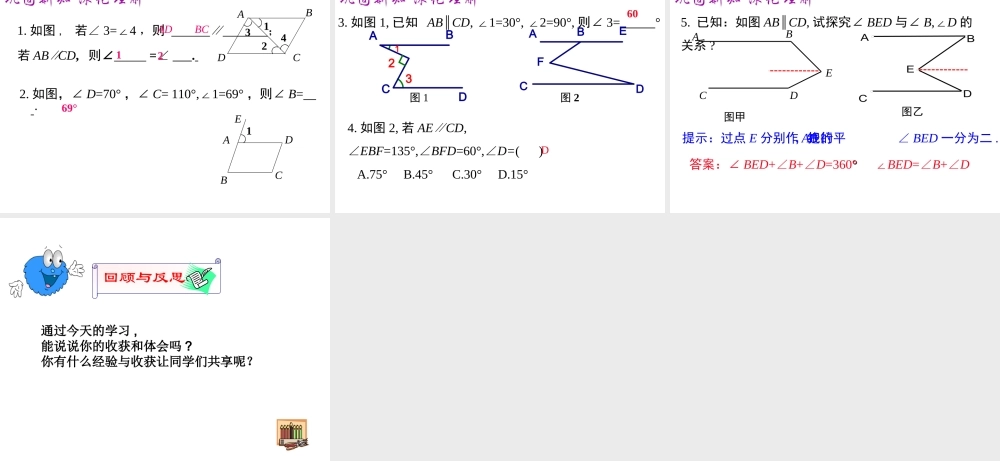
小结与复习第五章 相交线与平行线知识网络知识网络相交线一般情况邻补角对顶角邻补角互补对顶角相等特殊垂直存在性和唯一性垂线段最短点到直线的距离同位角、内错角、同旁内角平行线平行公理及其推论平行线的判定平行线的性质平移平移的特征命题知识构图两线四角三线八角专题复习专题复习【例 1 】如图 ,AB⊥CD 于点 O, 直线 EF 过 O 点 ,∠AOE=65°, 求∠ DOF 的度数 .BACDFEO解: AB⊥CD ,∴∠ AOC=90°. ∠AOE=65°,∴∠COE=25°又 ∠ COE=∠DOF( 对顶角相等)∴∠DOF=25°.专题一 相交线【迁移应用 1 】如图 ,AB,CD 相交于点O,∠AOC=70°,EF 平分∠COB, 求∠ COE 的度数 .ABCDEFO答案:∠ COE=125°.【归纳拓展】两条直线相交包括垂直和斜交两种情形 . 相交时形成了两对对顶角和四对邻补角. 其中垂直是相交的特殊情况,它将一个周角分成了四个直角 .【例 2 】如图, AD 为△ ABC 的高,能表示点到直 线(线段)的距离的线段有( ) A.2 条 B.3 条 C.4 条 D.5 条答案:从图中可以看到共有三条,A 到 BC 的垂线段AD,B 到 AD 的垂线段BD,C 到 AD 的垂线段CD. BCDA专题二 点到直线的距离B 【迁移应用 2 】如图 AC⊥BC,CD⊥AB 于点 D,CD=4.8cm,AC=6cm,BC=8cm, 则点 C 到 AB 的距离是 cm; 点 A 到 BC 的距离是 cm; 点 B 到AC 的距离是 cm.DCBA【归纳拓展】点到直线的距离容易和两点之间的距离相混淆 . 当图形复杂不容易分析出是哪条线段时,准确掌握概念,抓住垂直这个关键点,认真分析图形是关键 .4.868【例 3 】 (1) 如图所示 ,1=72∠°,2=72∠°,3=60∠°, 求∠4 的度数 . 解: ∠ 1=2=72∠° ,∴a//b ( 内错角相等,两直线平行).∴∠3+4=180∠°. ( 两直线平行,同旁内角互补) ∠3=60° ,∴∠ 4=120°.4321ab专题三 平行线的性质和判定证明 : ∠DAC= ∠ACB ( 已知 ) ∴ AD//BC( 内错角相等, 两直线平行) ∠D+∠DFE=180°°( 已知 ) ∴ AD// EF( 同旁内角互补 , 两直线平行) ∴ EF// BC( 平行于同一条直线的两条直线互相平行 )(2) 已知∠∠ DACDAC=∠=∠ACBACB,∠,∠DD+∠+∠DFEDFE=180=180°°,, 求证 :EFEF////BC.BC.ABCDEF【迁移应用 3 】如图所示,把一张张方形纸片 ABCD沿 EF 折叠,若∠ EFG=50°, 求∠ DEG 的度数 .NMFGEDCBA答案: 100°.【归纳拓展】平行线的性质和...