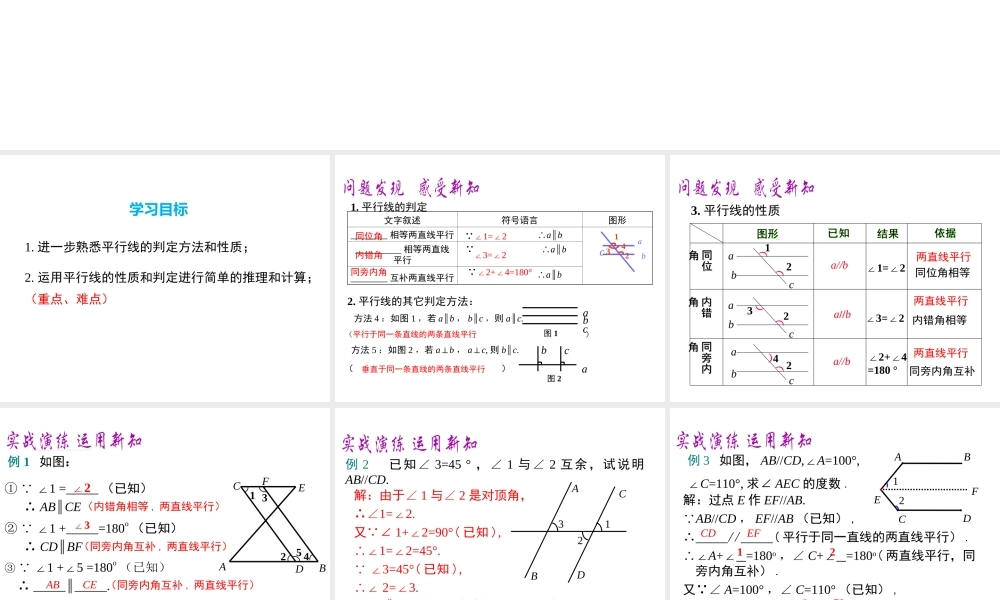
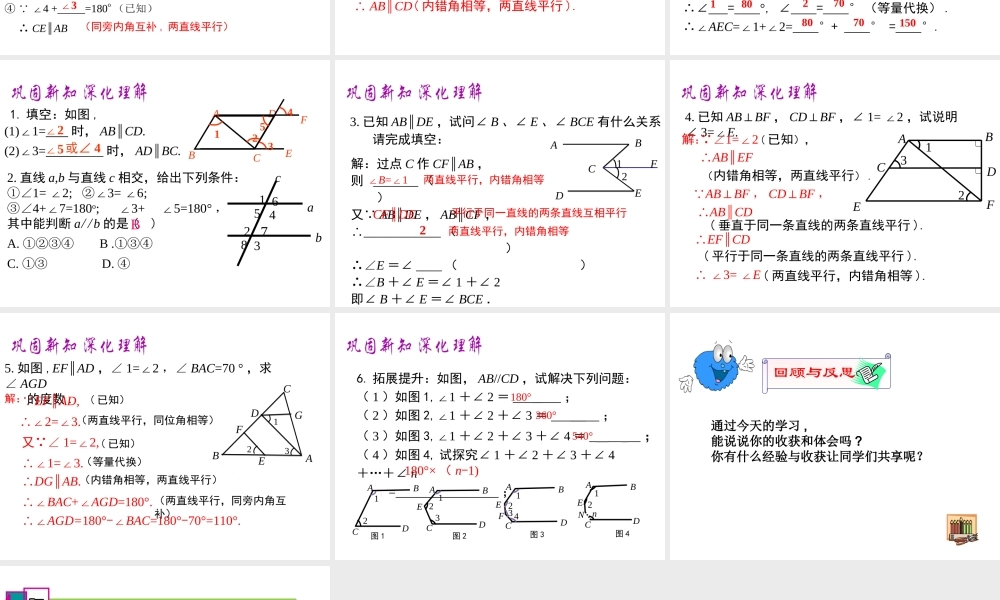
5.3 平行线的性质第五章 相交线与平行线5.3.1 平行线的性质第 2 课时 平行线的性质和判定及其综合运用2. 运用平行线的性质和判定进行简单的推理和计算;(重点、难点)学习目标1. 进一步熟悉平行线的判定方法和性质;文字叙述符号语言图形 相等两直线平行 ∴a b∥ 相等两直线平行 ∴a b∥ 互补两直线平行 ∴a b∥同位角内错角同旁内角 ∠1=2∠∠3=2∠ ∠2+4=180°∠abc12341. 平行线的判定 方法 4 :如图 1 ,若 a b∥ , b c∥ ,则 a c.∥( ) 方法 5 :如图 2 ,若 a⊥b , a⊥c, 则 b c.∥( )平行于同一条直线的两条直线平行 垂直于同一条直线的两条直线平行2. 平行线的其它判定方法:abc图 1abc图 2图形图形已知已知结果结果依据依据同位角 同位角内错角 内错角同旁内角 同旁内角122324))))))abababccca//b两直线平行同位角相等a//b两直线平行内错角相等同旁内角互补a//b两直线平行3. 平行线的性质∠1=∠2∠3=∠2∠2+∠4=180 ° ① ∠1 =_____ (已知) ∴ AB CE∥ ② ∠1 +_____=180o (已知) ∴ CD BF∥ ③ ∠1 +5 =180∠o (已知) ∴ _____∥_____.ABCE∠2 ④ ∠4 +_____=180o (已知) ∴ CE AB∥∠3∠3例 1 如图:1 35 42CFEADB(内错角相等 , 两直线平行)(同旁内角互补 , 两直线平行)(同旁内角互补 , 两直线平行)(同旁内角互补 , 两直线平行)例 2 已知∠ 3=45 ° ,∠ 1 与∠ 2 互余,试说明AB//CD. 解:由于∠ 1 与∠ 2 是对顶角,∴∠1=2.∠又 ∠ 1+2=90°∠( 已知 ),∴∠1=2=45°.∠ ∠3=45°( 已知 ), ∴∠ 2=3.∠ ∴ AB CD∥( 内错角相等,两直线平行 ).123ABCD例 3 如图, AB//CD,∠A=100°, ∠C=110°, 求∠ AEC 的度数 . EABCD21CDEF121280807070150F解:过点 E 作 EF//AB. AB//CD , EF//AB (已知) ,∴ // ( 平行于同一直线的两直线平行) .∴∠A+∠ =180o ,∠ C+∠ =180o( 两直线平行,同旁内角互补) .又 ∠ A=100° ,∠ C=110° (已知) , ∴∠ = °, ∠ = ° (等量代换) .∴∠AEC=1+2=∠∠ °+ ° = °. 1. 填空:如图 ,(1)1=∠ 时, AB CD.∥ (2)3=∠ 时, AD BC.∥D12345ABCFE∠2∠5或∠ 42. 直线 a,b 与直线 c 相交,给出下列条件:①∠1= 2; 3= 6;∠∠∠②③∠4+7=18...