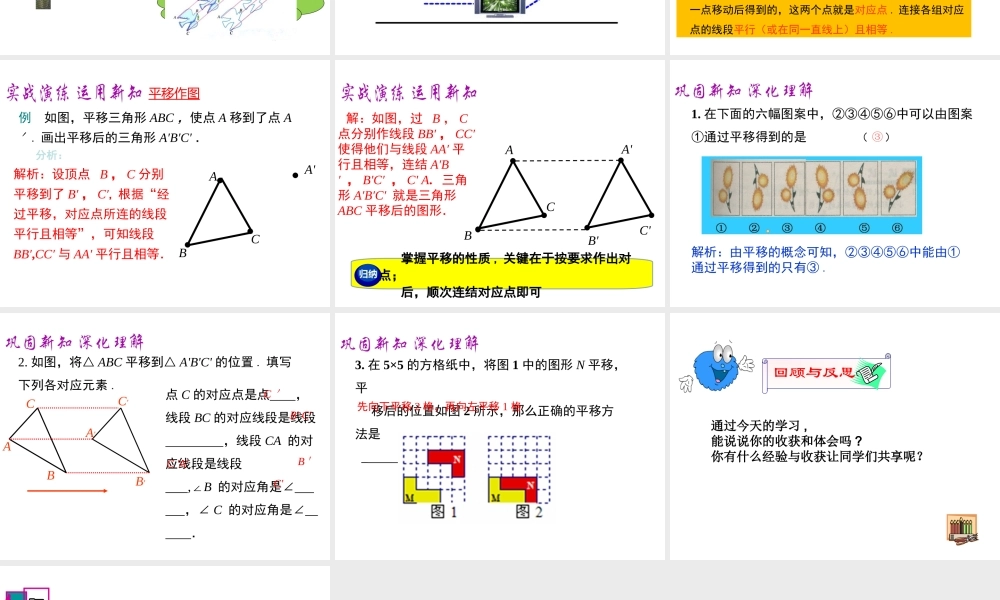
5.4 平 移第五章 相交线与平行线 1. 理解平移的定义及性质;(重点) 2. 会利用平移的性质进行简单的作图 . (难点) 学习目标仔细观察下面一些美丽的图案,它们有什么共同的特点?能否根据其中的一部分绘制出整个图案?如何在一张半透明的纸上,画出一排形状和大小如图的胡巴呢?“ 胡巴”的形状、大小、位置在运动前后是否发生了变化?形状不变,大小不变,位置改变平移的概念平移的概念:把一个图形整体沿某一直线方向移动,会得到一个新的图形.新图形与原图形的形状和大小完全相同.图形的这种移动,叫做平移 .辘轳上的水桶大厦里的电梯 生活中常见的平移图形的平移不一定是水平的,也不一定是竖直的 .它是沿某一直线方向移动的 .想一想:请看图片,平移是由什么决定的?由移动的方向和距离所决定 .思考:如图,在所画出的相邻两个胡巴中,找出三 组对应点 , 连接这些对应点,观察得出的线段 中,它们的位置,长短有什么关系?AA'BB'C'CAA'//BB'//CC'AA'=BB'=CC'平移的性质及平移作图 平移的性质:新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点就是对应点 . 连接各组对应点的线段平行(或在同一直线上)且相等 . 分析:解析:设顶点 B , C 分别平移到了 B′ , C′, 根据“经过平移,对应点所连的线段平行且相等”,可知线段 BB′,CC′ 与 AA′ 平行且相等.例 如图,平移三角形 ABC ,使点 A 移到了点 A′. 画出平移后的三角形 A′B′C′ .A'ABC平移作图 解:如图,过 B , C点分别作线段 BB′ , CC′ 使得他们与线段 AA′ 平行且相等,连结 A′B′ , B′C′ , C′ A. 三角形 A′B′C′ 就是三角形ABC 平移后的图形.B'C'A'ABC 掌握平移的性质 , 关键在于按要求作出对应点; 后,顺次连结对应点即可归纳1. 在下面的六幅图案中,②③④⑤⑥中可以由图案①通过平移得到的是 ( ) ③解析:由平移的概念可知,②③④⑤⑥中能由①通过平移得到的只有③ .点 C 的对应点是点 ,线段 BC 的对应线段是线段 ,线段 CA 的对应线段是线段 ,∠B 的对应角是∠ ,∠ C 的对应角是∠ .2. 如图,将△ ABC 平移到△ A'B'C' 的位置 . 填写下列各对应元素 . A′AB′BC'CC 'B' C'C 'A'B 'C'3. 在 5×5 的方格纸中,将图 1 中的图形 N 平移,平 移后的位置如图 2 所示,那么正确的平移方法是 .先向下平移 2 格,...