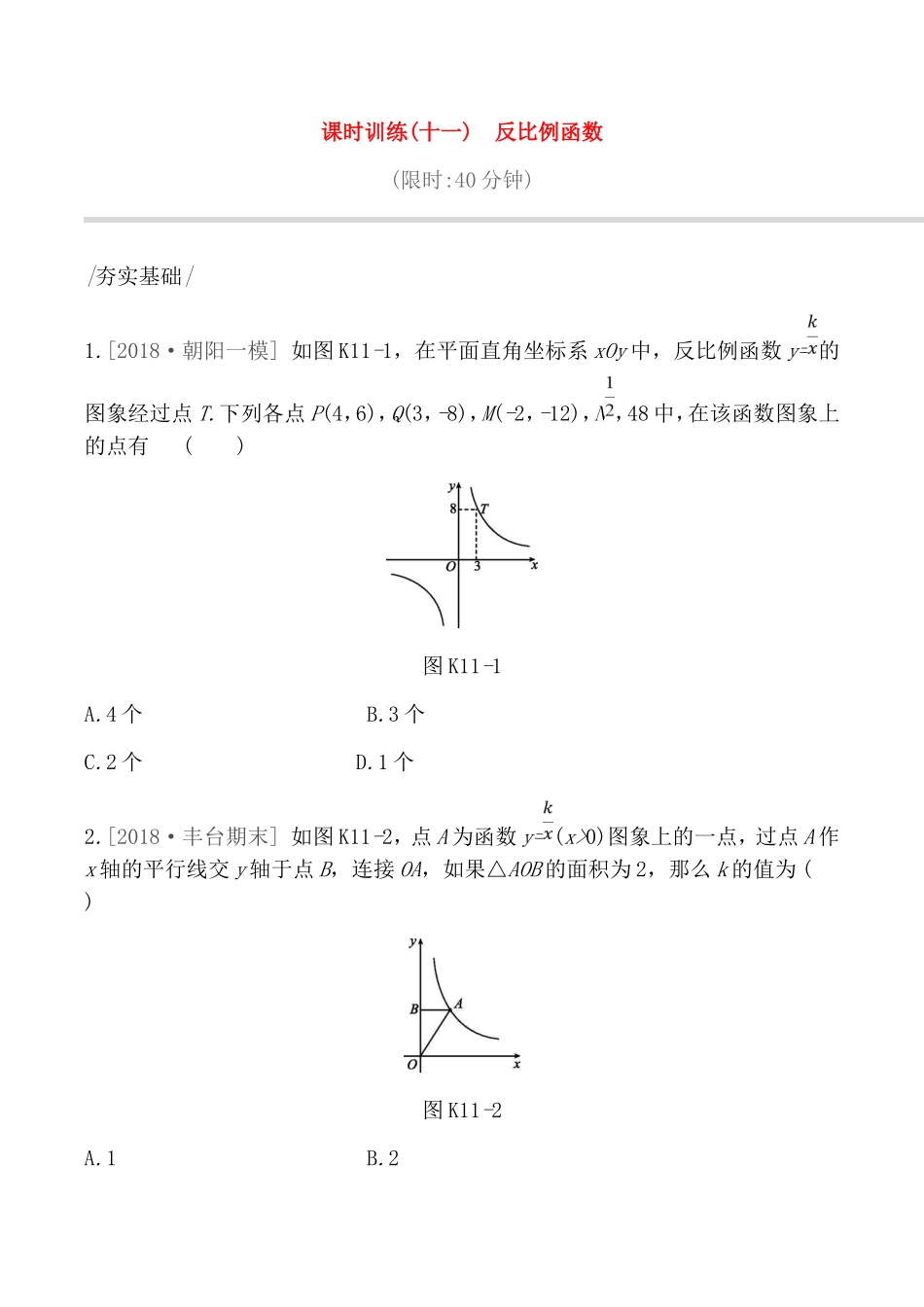
课时训练(十一)反比例函数(限时:40分钟)|夯实基础|1.[2018·朝阳一模]如图K11-1,在平面直角坐标系xOy中,反比例函数y=的图象经过点T.下列各点P(4,6),Q(3,-8),M(-2,-12),N,48中,在该函数图象上的点有()图K11-1A.4个B.3个C.2个D.1个2.[2018·丰台期末]如图K11-2,点A为函数y=(x>0)图象上的一点,过点A作x轴的平行线交y轴于点B,连接OA,如果△AOB的面积为2,那么k的值为()图K11-2A.1B.2C.3D.43.[2018·燕山期末]若点(x1,y1),(x2,y2)都是反比例函数y=图象上的点,并且y1<0x2B.x1y2,则x1-x2的值是()A.正数B.负数C.非正数D.不能确定5.如图K11-3,A,B两点在双曲线y=上,分别过A,B两点向坐标轴作垂线段,已知S阴影=1,则S1+S2=()图K11-3A.3B.4C.5D.66.如图K11-4,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数y=在第一象限内的图象与△ABC有交点,则k的取值范围是()图K11-4A.2≤k≤B.6≤k≤10C.2≤k≤6D.2≤k≤7.[2018·平谷期末]请写出一个过点(1,1),且与x轴无交点的函数表达式.8.下列关于反比例函数y=的三个结论:①它的图象经过点(7,3);②它的图象在每一个象限内,y随x的增大而减小;③它的图象在第二、四象限内.其中正确的是(填序号即可).9.对于反比例函数y=-,当x<2时,y的取值范围是.10.[2018·门头沟期末]如图K11-5,在平面直角坐标系xOy中有一矩形,顶点坐标分别为(1,1),(4,1),(4,3),(1,3),有一反比例函数y=(k≠0),它的图象与此矩形没有交点,该表达式可以为.图K11-511.[2018·门头沟初三综合练习]如图K11-6,在平面直角坐标系xOy中,一次函数y=x与反比例函数y=(k≠0)的图象相交于点A(,a).(1)求a,k的值;(2)直线x=b(b>0)分别与一次函数y=x、反比例函数y=的图象相交于点M,N,当MN=2时,画出示意图并直接写出b的值.图K11-6|拓展提升|12.[2018·东城期末]如图K11-7,在平面直角坐标系xOy中,已知A(8,0),C(0,6),矩形OABC的对角线交于点P,点M在经过点P的函数y=(x>0)的图象上运动,k的值为,OM长的最小值为.图K11-713.[2018·海淀期末]如图K11-8,函数y=(x<0)与y=ax+b的图象交于点A(-1,n)和点B(-2,1).(1)求k,a,b的值;(2)直线x=m与y=(x<0)的图象交于点P,与y=-x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.图K11-814.[2018·海淀一模]在平面直角坐标系xOy中,已知点P(2,2),Q(-1,2),函数y=.(1)当函数y=的图象经过点P时,求m的值并画出直线y=x+m;(2)若P,Q两点中恰有一个点的坐标(x,y)满足不等式组(m>0),求m的取值范围.图K11-9参考答案1.B2.D3.B4.D5.D6.A[解析]反比例函数的图象和三角形有交点的第一个临界点是交点A,∵过点A(1,2)的反比例函数的解析式为y=,∴k≥2.随着k的增大,反比例函数的图象必须和直线BC有交点才能满足题意,经过B(2,5),C(6,1)的直线的函数解析式为y=-x+7,由得x2-7x+k=0,根据Δ≥0,得k≤.综上可知2≤k≤.7.答案不唯一,如:y=8.①②9.y<-4或y>010.答案不唯一,满足k<0或012均可11.解:(1)∵直线y=x与双曲线y=(k≠0)相交于点A(,a).∴a=,∴A(,),∴=,解得k=3.(2)画图略.b=3或1.12.12213.解:(1)∵函数y=(x<0)的图象经过点B(-2,1),∴=1,得k=-2.∵函数y=(x<0)的图象还经过点A(-1,n),∴n==2,点A的坐标为(-1,2).∵函数y=ax+b的图象经过点A和点B,∴解得(2)-20)时,解不等式组得00)时,解不等式组得m>3.∵P,Q两点中恰有一个点的坐标满足(m>0),∴m的取值范围是:0