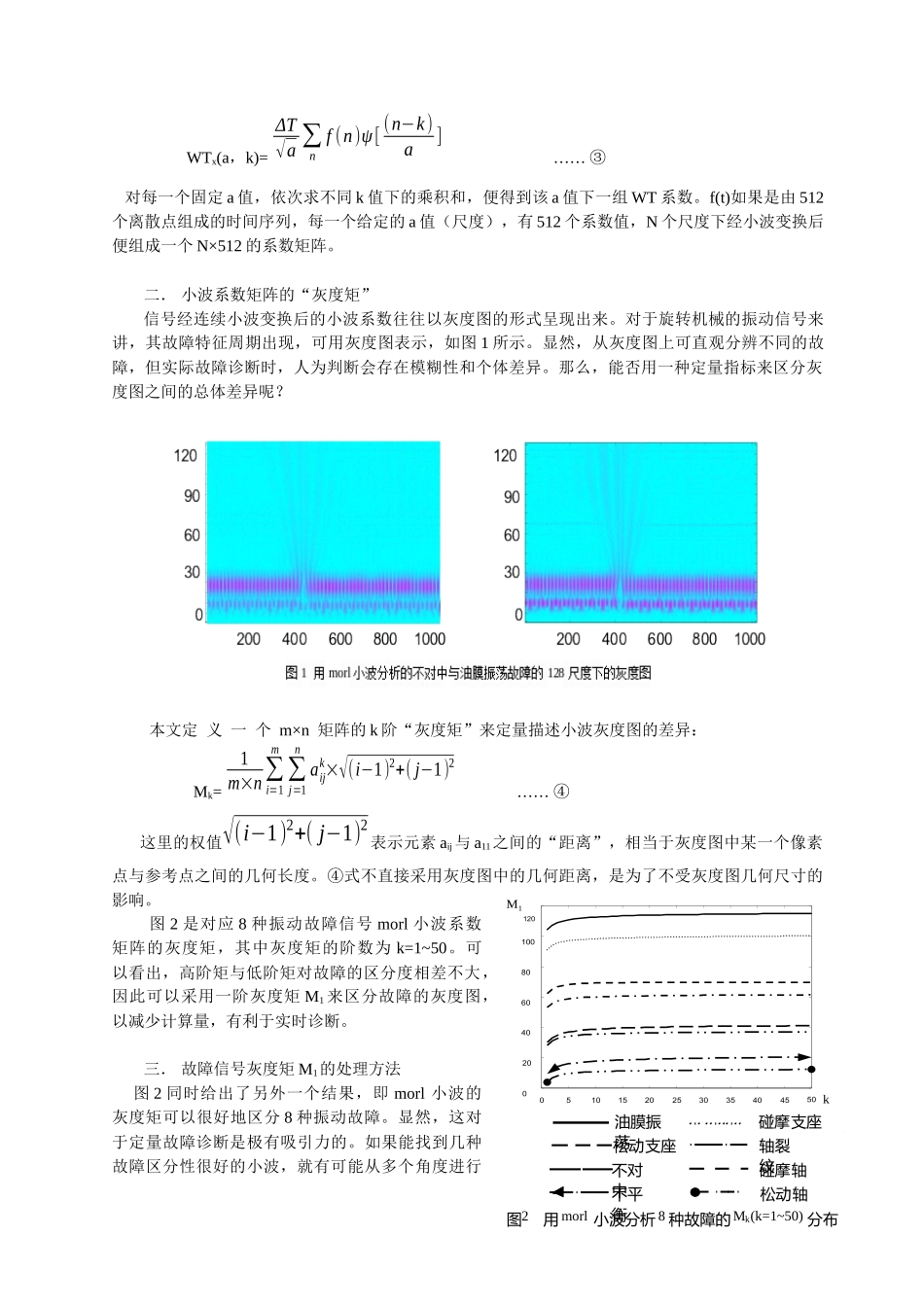
基于小波分析的旋转机械振动信号定量特征研究1侯敬宏黄树红申弢张燕平(华中科技大学能源与动力工程学院武汉430074)摘要:通过对机械振动信号的连续小波变换,利用小波滤波器良好的时频特性,研究了振动信号经过连续小波变换后的统计特征。在信号的特征提取中,引入“灰度矩”并把一阶矩作为定量指标。对8种典型故障信号的研究表明,这种方法能够简单有效地提取信号的特征,区分振动故障。关键词:小波变换;故障诊断;信号处理;特征提取中图分类号TH165.3文献标识码A现有的旋转机械振动信号的分析方法多只是定性指出机组可能存在的故障,而现实中并不是设备存在隐患就立即停机处理,而是希望根据定量评价故障的危害程度以及发展趋势而作决定,从而有效避免“维修不足”和“过剩维修”所带来的经济损失。小波滤波器是一个具有恒Q(品质因子,定义为滤波器的中心频率与带宽之比)特性的滤波器,因此,其可以随信号频率增高而减小时窗宽度并相应增加频窗宽度,即具有”变焦”分析的特性。故而小波分析在信号的时频分析中具有特殊的地位和性能。从数学上看,对机械振动信号进行小波分析,是将一维信号在二维空间进行分解,使得在一维空间中无法提取的特征在二维空间中得到很好的反映。从物理上看,对振动信号进行连续小波变换和分析,实际上就是将无法从一维时域或者频域中体现的信号特征,在具有良好滤波器特性的小波时频窗中得以体现,以获得信号所包含的特征信息[3]。因此,分析机械振动信号的连续小波系数,从中提取特征,可以更好地反映信号的本质。利用连续小波分析信号时,一般用每个尺度下小波能谱图提取信号的定性特征。这在很大程度上依赖于人的主观判断。如果要实现自主式的状态诊断,则必须要提取能反映信号特征的定量指标。本文引入一种“灰度矩”的统计量,对8种故障信号波形经连续小波变换后的系数矩阵进行处理,提出区分这些故障的定量指标。所选取的8种故障信号为[2]:不平衡,不对中,油膜振荡,轴裂纹,支座松动的轴振动信号,支座松动的支座振动信号,碰摩故障的轴振动信号,碰摩故障的支座振动信号。本文所采用的所有故障信号均为本单位模拟试验台的实验数据。一.连续小波变换一般所讨论的小波,是指一个被称之为母小波或基本小波的函数,经伸缩和平移所产生的函数簇Ψa,b(t),式中a>0是尺度因子,b反映位移,其值可正可负。定义满足“容许条件”[1]:∫0∞|ψ(ω)|2ωdω<∞……①的函数Ψ(t)为基本小波函数,简称小波函数。若函数f(t)是平方可积函数,即∫|f(t)|2dt<∞,定义:WTx(a,b)=1√a∫f(t)ψ¿(t−ba)dt=……②为f(t)的小波变换。上标*代表共轭,代表内积。要实现WTx(a,b)所定义的内积,除少数情况可做解析计算外,大多数情况只能通过计算机做近似数值计算。按数字信号处理的习惯可将式②变成:1国家自然科学基金项目(50105004)05101520253035404550020406080100120M1k图2用morl小波分析8种故障的Mk(k=1~50)分布油膜振荡碰摩-支座松动-支座轴裂纹不对中碰摩-轴不平衡松动-轴WTx(a,k)=ΔT√a∑nf(n)ψ[(n−k)a]……③对每一个固定a值,依次求不同k值下的乘积和,便得到该a值下一组WT系数。f(t)如果是由512个离散点组成的时间序列,每一个给定的a值(尺度),有512个系数值,N个尺度下经小波变换后便组成一个N×512的系数矩阵。二.小波系数矩阵的“灰度矩”信号经连续小波变换后的小波系数往往以灰度图的形式呈现出来。对于旋转机械的振动信号来讲,其故障特征周期出现,可用灰度图表示,如图1所示。显然,从灰度图上可直观分辨不同的故障,但实际故障诊断时,人为判断会存在模糊性和个体差异。那么,能否用一种定量指标来区分灰度图之间的总体差异呢?本文定义一个m×n矩阵的k阶“灰度矩”来定量描述小波灰度图的差异:Mk=1m×n∑i=1m∑j=1naijk×√(i−1)2+(j−1)2……④这里的权值√(i−1)2+(j−1)2表示元素aij与a11之间的“距离”,相当于灰度图中某一个像素点与参考点之间的几何长度。④式不直接采用灰度图中的几何距离,是为了不受灰度图几何尺寸的影响。图2是对应8种振动故障信号morl小波系数矩阵的灰度矩,...