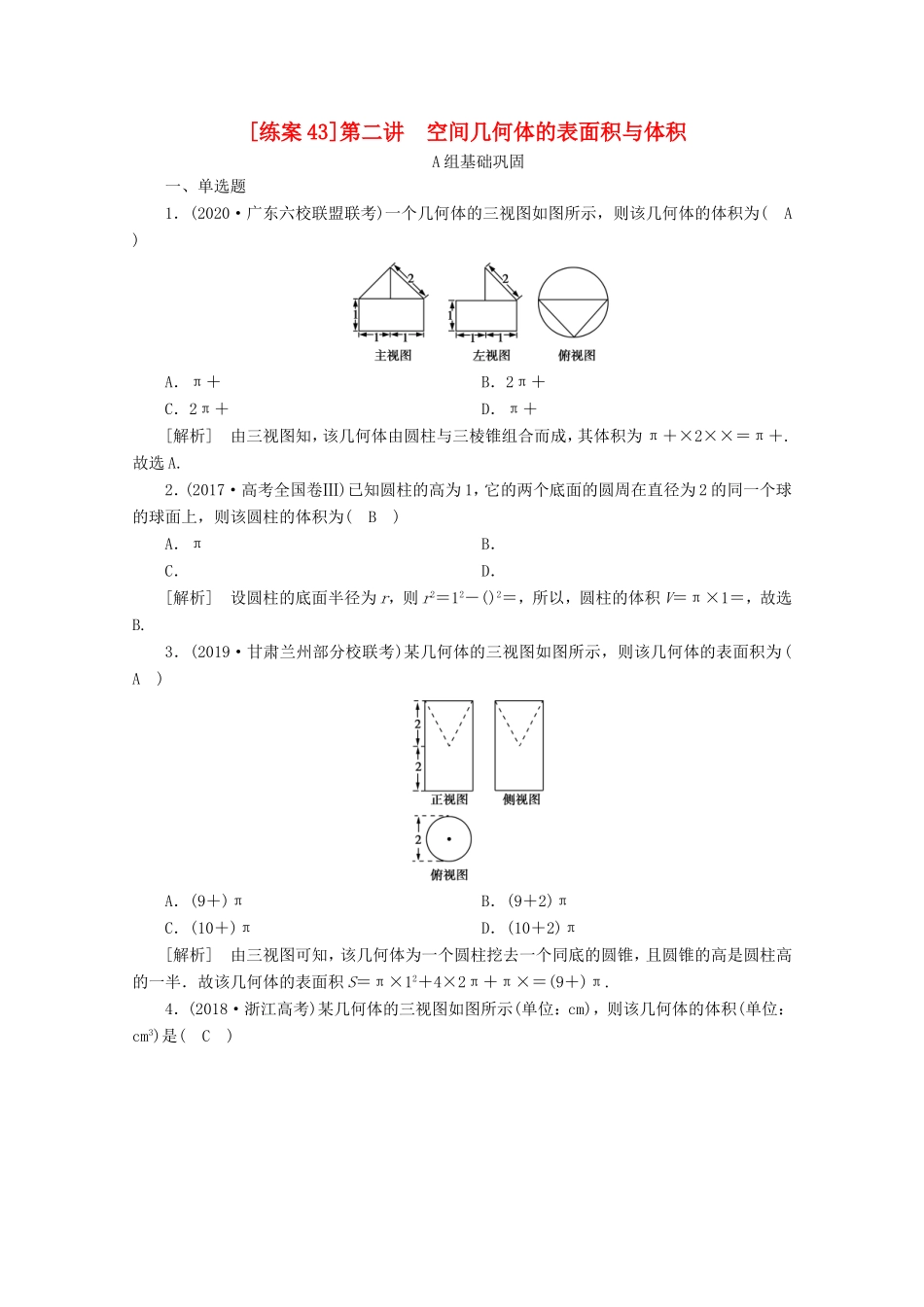
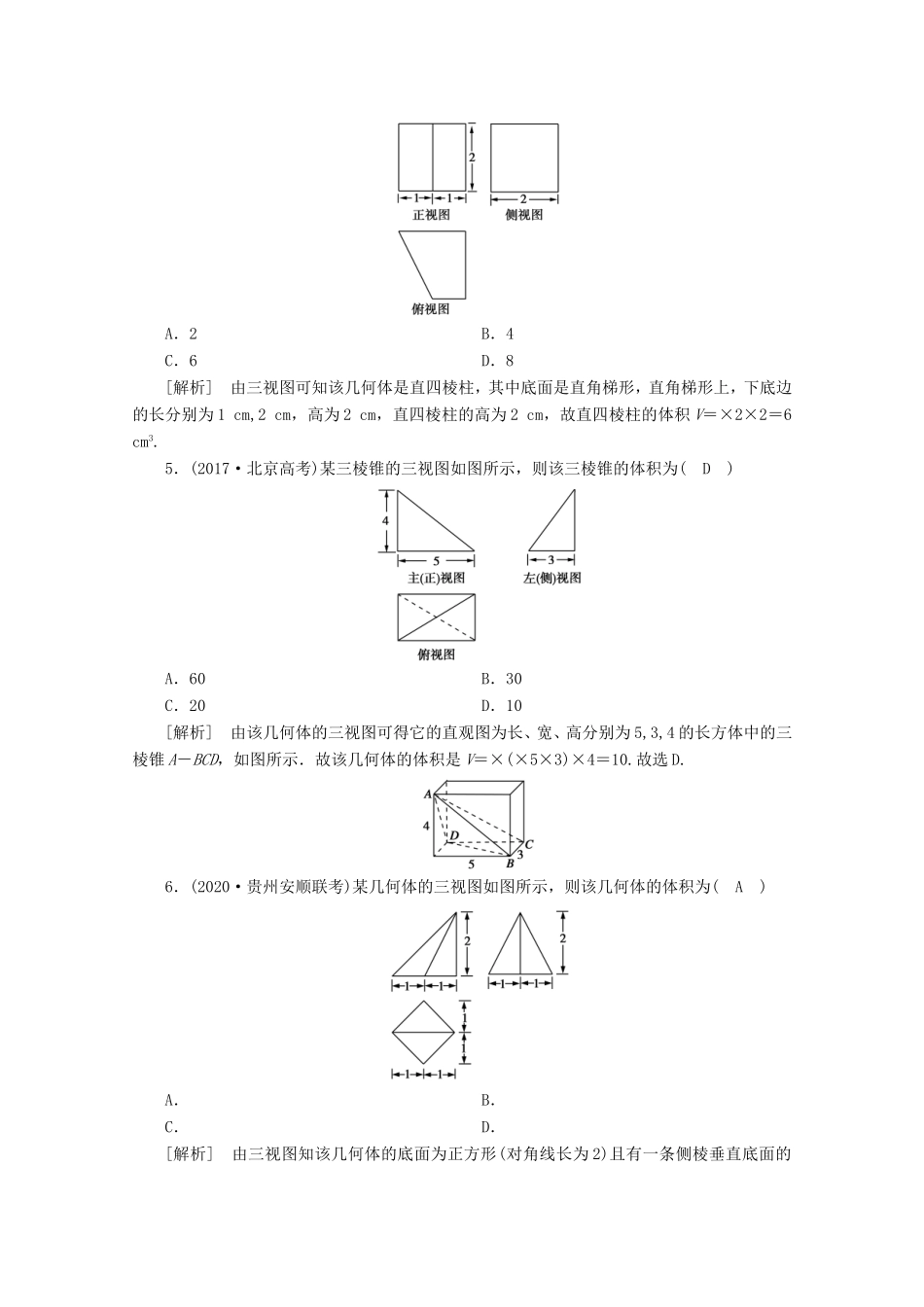
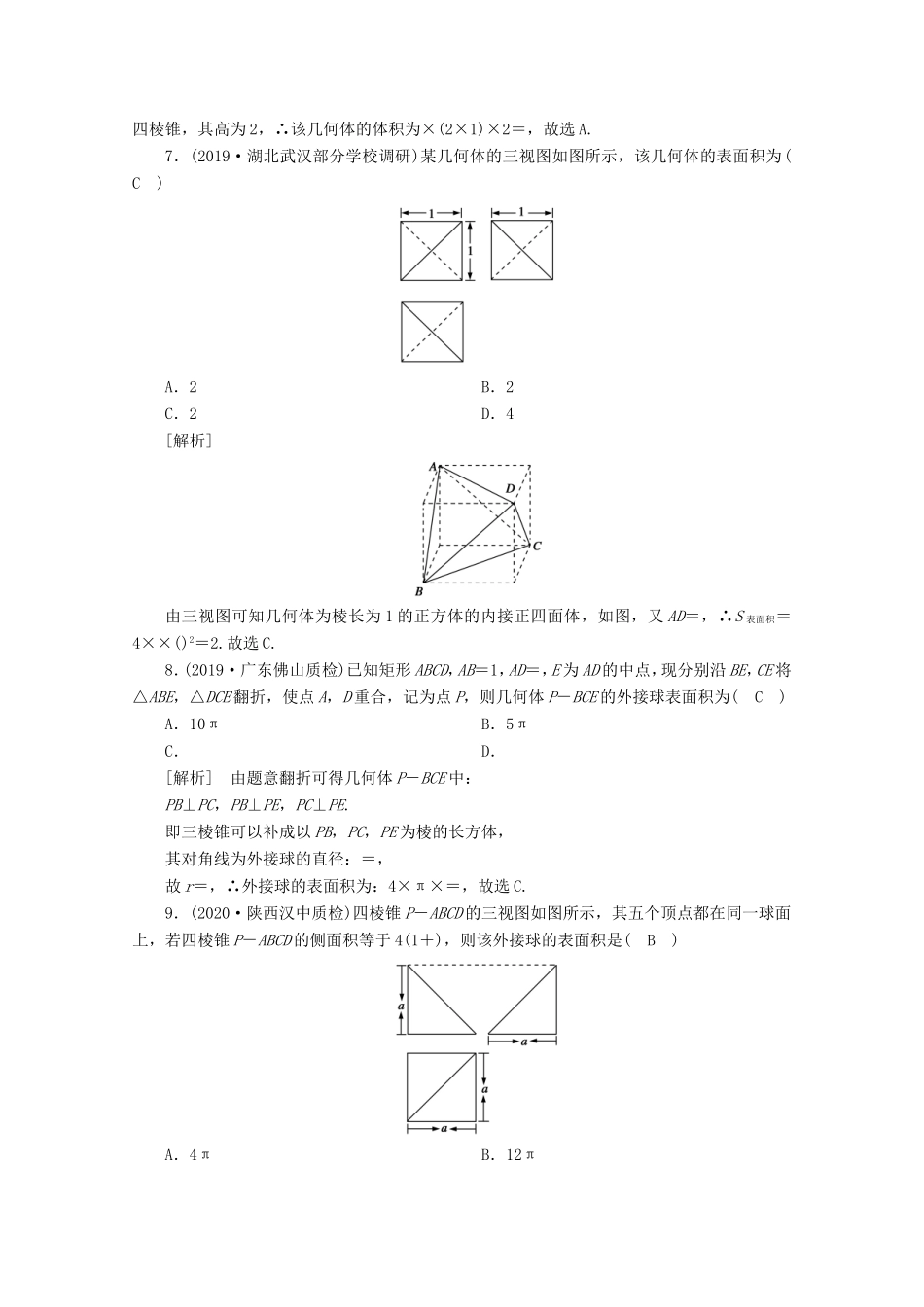
[练案43]第二讲空间几何体的表面积与体积A组基础巩固一、单选题1.(2020·广东六校联盟联考)一个几何体的三视图如图所示,则该几何体的体积为(A)A.π+B.2π+C.2π+D.π+[解析]由三视图知,该几何体由圆柱与三棱锥组合而成,其体积为π+×2××=π+.故选A.2.(2017·高考全国卷Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为(B)A.πB.C.D.[解析]设圆柱的底面半径为r,则r2=12-()2=,所以,圆柱的体积V=π×1=,故选B.3.(2019·甘肃兰州部分校联考)某几何体的三视图如图所示,则该几何体的表面积为(A)A.(9+)πB.(9+2)πC.(10+)πD.(10+2)π[解析]由三视图可知,该几何体为一个圆柱挖去一个同底的圆锥,且圆锥的高是圆柱高的一半.故该几何体的表面积S=π×12+4×2π+π×=(9+)π.4.(2018·浙江高考)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是(C)A.2B.4C.6D.8[解析]由三视图可知该几何体是直四棱柱,其中底面是直角梯形,直角梯形上,下底边的长分别为1cm,2cm,高为2cm,直四棱柱的高为2cm,故直四棱柱的体积V=×2×2=6cm3.5.(2017·北京高考)某三棱锥的三视图如图所示,则该三棱锥的体积为(D)A.60B.30C.20D.10[解析]由该几何体的三视图可得它的直观图为长、宽、高分别为5,3,4的长方体中的三棱锥A-BCD,如图所示.故该几何体的体积是V=×(×5×3)×4=10.故选D.6.(2020·贵州安顺联考)某几何体的三视图如图所示,则该几何体的体积为(A)A.B.C.D.[解析]由三视图知该几何体的底面为正方形(对角线长为2)且有一条侧棱垂直底面的四棱锥,其高为2,∴该几何体的体积为×(2×1)×2=,故选A.7.(2019·湖北武汉部分学校调研)某几何体的三视图如图所示,该几何体的表面积为(C)A.2B.2C.2D.4[解析]由三视图可知几何体为棱长为1的正方体的内接正四面体,如图,又AD=,∴S表面积=4××()2=2.故选C.8.(2019·广东佛山质检)已知矩形ABCD,AB=1,AD=,E为AD的中点,现分别沿BE,CE将△ABE,△DCE翻折,使点A,D重合,记为点P,则几何体P-BCE的外接球表面积为(C)A.10πB.5πC.D.[解析]由题意翻折可得几何体P-BCE中:PB⊥PC,PB⊥PE,PC⊥PE.即三棱锥可以补成以PB,PC,PE为棱的长方体,其对角线为外接球的直径:=,故r=,∴外接球的表面积为:4×π×=,故选C.9.(2020·陕西汉中质检)四棱锥P-ABCD的三视图如图所示,其五个顶点都在同一球面上,若四棱锥P-ABCD的侧面积等于4(1+),则该外接球的表面积是(B)A.4πB.12πC.24πD.36π[解析]根据三视图可在棱长为a的正方体中得到直观图,是一个四棱锥P-ABCD,如图所示:则四棱锥的侧面积为:S△PAB+S△PAD+S△PBC+S△PDC=a2+a2+a·a+a·,根据已知侧面积可得:(+1)a2=4(+1),解得:a=2,设PC的中点为O,则OA=OB=OC=OD=OP==,所以四棱锥的外接球的半径R=,所以该外接球的表面积为4πR2=4π×()2=12π,故选B.二、多选题10.一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是(BCD)A.三角形B.长方形C.正方形D.正六边形11.(原创)两直角边长分别为6、8的直角三角形绕其一边所在直线旋转一周,所形成的几何体的体积可能为(ABC)A.96πB.128πC.πD.12.(2020·陕西商洛期末改编)已知正四棱柱ABCD-A1B1C1D1的每个顶点都在球的O球面上,若球O的表面积为12π,则该四棱柱的侧面积的值可能为(ABC)A.10B.12C.16D.18[解析]设球O的半径为R,则4πR2=12π,得R=.设正四棱柱的底面边长为x,高为h,则正四棱柱的体对角线即为球O的直径,则有=2R=2,即2x2+h2=12,由基本不等式可得12=2x2+h2≥2xh,xh≤3,当且仅当h=x时,等号成立,因此,该四棱柱的侧面积为4xh≤4×3=12,即四棱柱的侧面积得取值范围为(0,12],故选ABC.三、填空题13.(2018·天津高考)如图,已知正方体ABCD-A1B1C1D1的棱长为1,则四棱锥A1-BB1D1D的体积为.[解析]本题主要考查正方体的性质和四棱锥的体积.四棱锥的底面BB1D1D为矩形,其面积为1×...