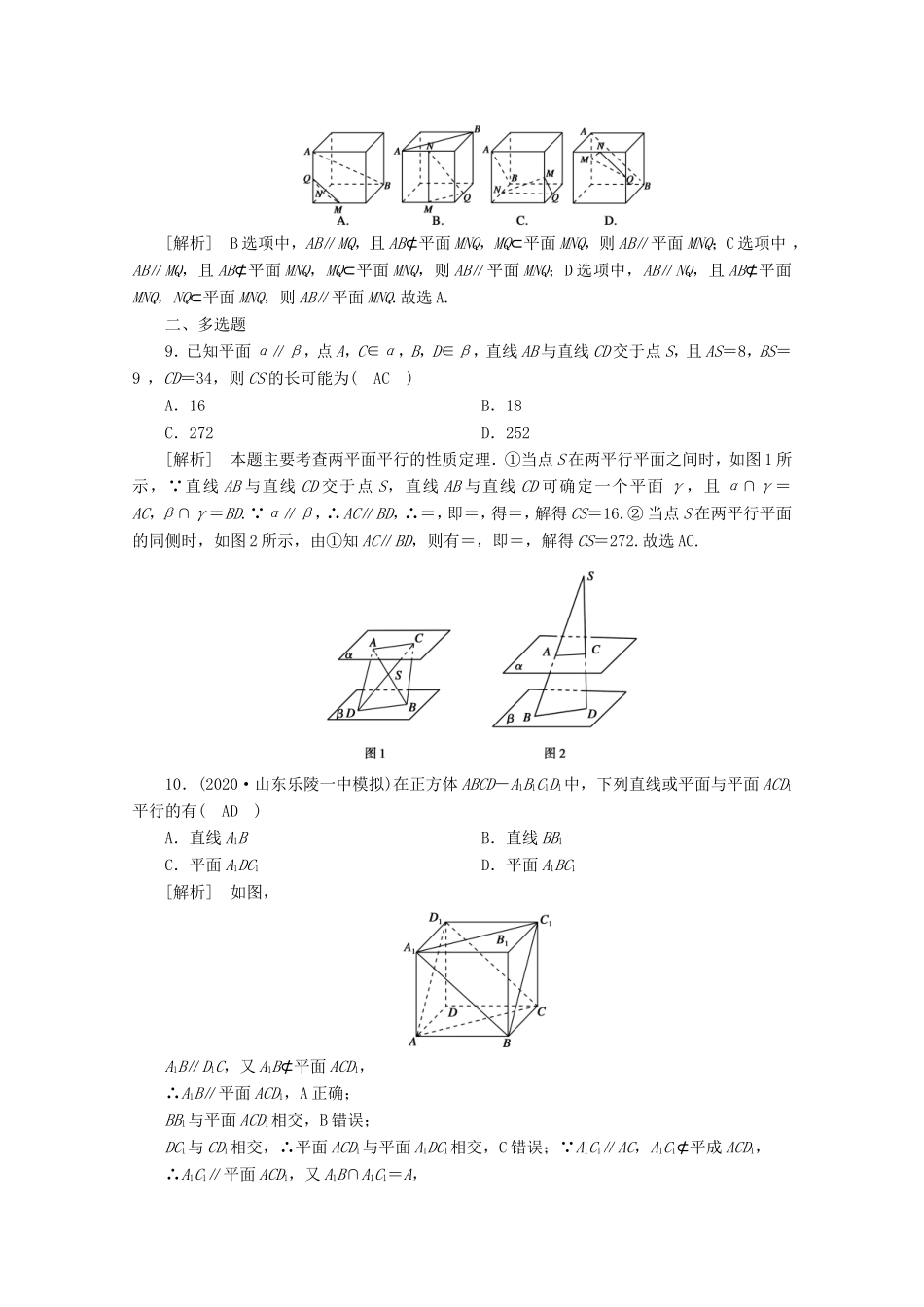
[练案45]第四讲直线、平面平行的判定与性质A组基础巩固一、单选题1.(2020·河南省开封市模拟)已知直线m,n和平面α,n⊂α,则“m∥n”是“m∥α”的(D)A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件[解析]n⊂α,m∥n,当m⊂α时,m∥α,m∥α,n⊂α⇒m∥n或m、n异面即m∥n,故“m∥n”是“m∥α”的既不充分也不必要条件.2.(2020·辽宁沈阳东北育才学校模拟)在空间中,下列命题中为真命题的是(D)A.垂直于同一直线的两条直线平行B.平行于同一平面的两条直线平行C.垂直于同一平面的两个平面平行D.平行于同一平面的两个平面平行3.(2019·陕西西安模拟)在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE︰EB=AF︰FD=1︰4,H,G分别是BC,CD的中点,则(B)A.BD∥平面EFG,且四边形EFGH是平行四边形B.EF∥平面BCD,且四边形EFGH是梯形C.HG∥平面ABD,且四边形EFGH是平行四边形D.EH∥平面ADC,且四边形EFGH是梯形[解析]如图,由条件知EF∥BD,EF=BD,HG∥BD,HG=BD,∴EF∥HG且EF=HG,∴四边形EFGH为梯形, EF∥BD,EF⊄平面BCD,BD⊂平面BCD,∴EF∥平面BCD.故选B.4.(2019·青岛二模)已知m,n是两条不重合的直线,α,β,γ是三个不重合的平面,则α∥β的一个充分条件是(D)A.m∥α,m∥βB.α⊥γ,β⊥γC.m⊂α,n⊂β,m∥nD.m,n是异面直线,m⊂α,m∥β,n⊂β,n∥α[解析]A中,α,β可能相交,故错误;B不正确,如正方体中过同一个顶点的三个平面的关系;C中α,β可能相交,故错误;根据直线与平面平行的性质定理及平面与平面平行的判定定理可知D正确.5.(2019·山东泰安期末)有两条不同的直线m,n与两个不同的平面α,β,下列命题正确的是(A)A.m⊥α,n∥β,且α∥β,则m⊥nB.m⊥α,n⊥β,且α⊥β,则m∥nC.m∥α,n⊥β,且α⊥β,则m∥nD.m∥α,n∥β,且α∥β,则m∥n[解析]对于A,由m⊥α,n∥β,且α∥β得m⊥n,故正确;对于B,由m⊥α,n⊥β,α⊥β得m⊥n,故错误;对于C,由m∥α,n⊥β,且α⊥β得m∥n或m,n相交或异面,故错误;对于D,由m∥α,n∥β,且α∥β得m,n的关系可以是相交或平行或异面,故错误.故选A.6.若P为异面直线a,b外一点,则过P且与a,b均平行的平面(B)A.不存在B.零个或一个C.可以有两个D.有无数多个[解析]记a与P所确定的平面为α,当b∥α时,与a,b均平行的平面不存在,当b不平行α时,与a,b均平行的平面有一个,故选B.7.(2019·衡水中学调研卷)如图,P为平行四边形ABCD所在平面外一点,E为AD的中点,F为PC上—点,当PA∥平面EBF时,=(D)A.B.C.D.[解析]连接AC交BE于点G,连接FG,因为PA∥平面EBF,PA⊂平面PAC,平面PAC∩平面EBF=FG,所以PA∥FG,所以=.因为AD∥BC,AD=BC,E为AD的中点,所以==,所以=.8.(2017·课标全国Ⅰ)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是(A)[解析]B选项中,AB∥MQ,且AB⊄平面MNQ,MQ⊂平面MNQ,则AB∥平面MNQ;C选项中,AB∥MQ,且AB⊄平面MNQ,MQ⊂平面MNQ,则AB∥平面MNQ;D选项中,AB∥NQ,且AB⊄平面MNQ,NQ⊂平面MNQ,则AB∥平面MNQ.故选A.二、多选题9.已知平面α∥β,点A,C∈α,B,D∈β,直线AB与直线CD交于点S,且AS=8,BS=9,CD=34,则CS的长可能为(AC)A.16B.18C.272D.252[解析]本题主要考查两平面平行的性质定理.①当点S在两平行平面之间时,如图1所示, 直线AB与直线CD交于点S,直线AB与直线CD可确定一个平面γ,且α∩γ=AC,β∩γ=BD. α∥β,∴AC∥BD,∴=,即=,得=,解得CS=16.②当点S在两平行平面的同侧时,如图2所示,由①知AC∥BD,则有=,即=,解得CS=272.故选AC.10.(2020·山东乐陵一中模拟)在正方体ABCD-A1B1C1D1中,下列直线或平面与平面ACD1平行的有(AD)A.直线A1BB.直线BB1C.平面A1DC1D.平面A1BC1[解析]如图,A1B∥D1C,又A1B⊄平面ACD1,∴A1B∥平面ACD1,A正确;BB1与平面ACD1相交,B错误;DC1与CD1相交,∴平面ACD1与平面A1DC1相交,C错误; A1C1∥AC,A1C1⊄平成A...