高考数学一轮复习 练案（48）第七章 立体几何 第七讲 立体几何中的向量方法（含解析）-人教版高三数学试题VIP专享VIP免费

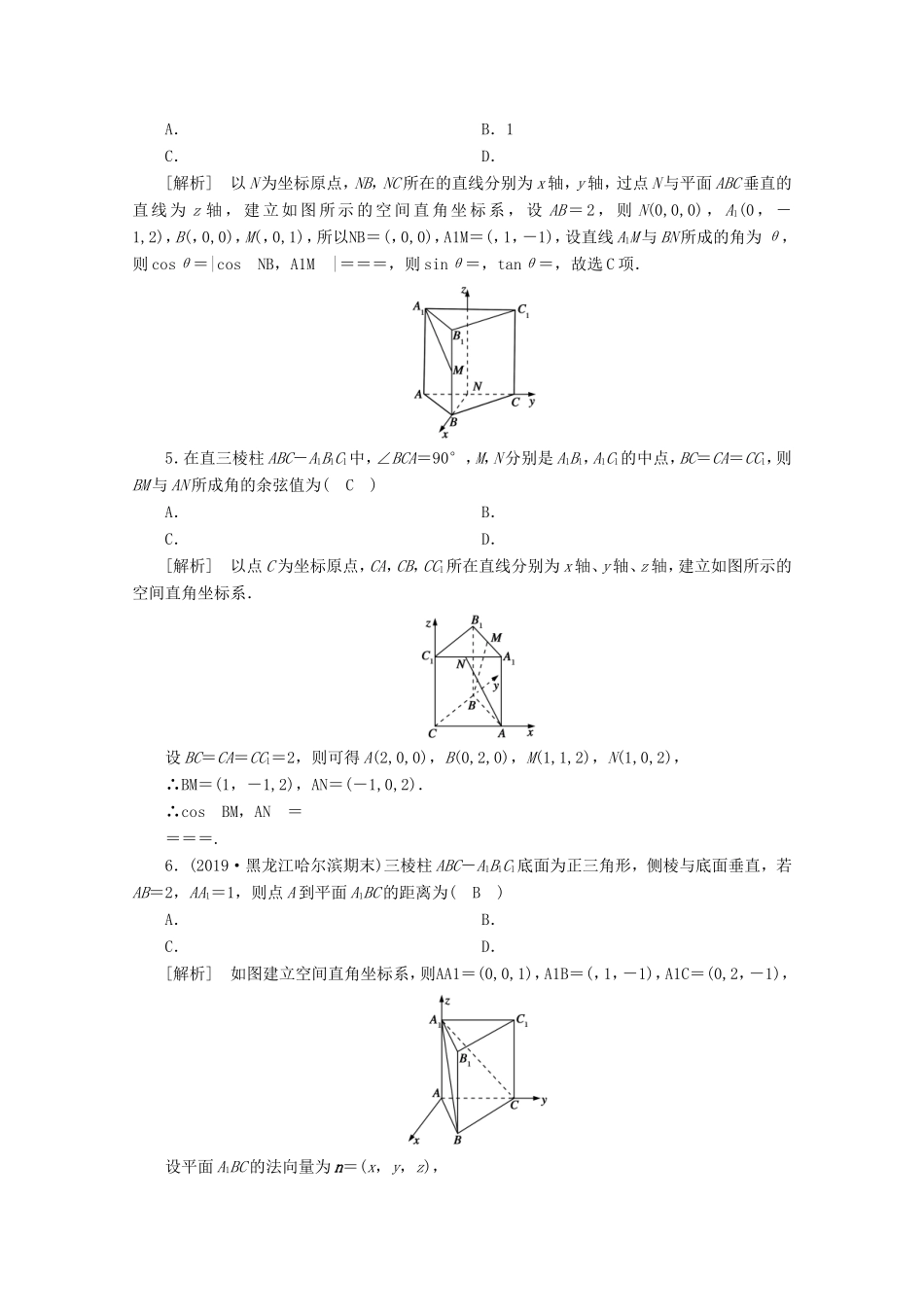
[练案48]第七讲立体几何中的向量方法A组基础巩固一、单选题1．(2020·东营质检)已知A(1,0,0)，B(0，－1,1)，OA＋λOB与OB的夹角为120°，则λ的值为(C)A．±B．C．－D．±[解析]OA＋λOB＝(1，－λ，λ)，cos120°＝＝－，得λ＝±.经检验λ＝不合题意，舍去，∴λ＝－.2．在空间直角坐标系O－xyz中，平面OAB的法向量为a＝(2，－2,1)，已知P(－1,3,2)，则P到平面OAB的距离等于(B)A．4B．2C．3D．1[解析]设点P到平面OAB的距离为d，则d＝，因为a＝(2，－2,1)，P(－1,3,2)，所以d＝＝2.故选B.3．如图所示，正方体ABCD－A1B1C1D1中，M，N分别为下底面ABCD和上底面A1B1C1D1的中心，则B1M与AN所成角的余弦值等于(B)A．－B．C．－D．[解析]如图，以D为坐标原点，分别以DA，DC，DD1所在直线为x轴，y轴，z轴建立空间直角坐标系D－xyz.设AB＝2，B1M与AN所成角为θ，则A(2,0,0)，M(1,1,0)，B1(2,2,2)，N(1,1,2)，所以AN＝(－1,1,2)，B1M＝(－1，－1，－2)．故cosAN，B1M＝＝＝－.因为两异面直线所成角的范围是(0，]，所以cosθ＝.故选B.4．在各棱长均相等的直三棱柱ABC－A1B1C1中，已知M是棱BB1的中点，N是棱AC的中点，则异面直线A1M与BN所成角的正切值为(C)A．B．1C．D．[解析]以N为坐标原点，NB，NC所在的直线分别为x轴，y轴，过点N与平面ABC垂直的直线为z轴，建立如图所示的空间直角坐标系，设AB＝2，则N(0,0,0)，A1(0，－1,2)，B(，0,0)，M(，0,1)，所以NB＝(，0,0)，A1M＝(，1，－1)，设直线A1M与BN所成的角为θ，则cosθ＝|cosNB，A1M|＝＝＝，则sinθ＝，tanθ＝，故选C项．5．在直三棱柱ABC－A1B1C1中，∠BCA＝90°，M，N分别是A1B1，A1C1的中点，BC＝CA＝CC1，则BM与AN所成角的余弦值为(C)A．B．C．D．[解析]以点C为坐标原点，CA，CB，CC1所在直线分别为x轴、y轴、z轴，建立如图所示的空间直角坐标系．设BC＝CA＝CC1＝2，则可得A(2,0,0)，B(0,2,0)，M(1,1,2)，N(1,0,2)，∴BM＝(1，－1,2)，AN＝(－1,0,2)．∴cosBM，AN＝＝＝＝.6．(2019·黑龙江哈尔滨期末)三棱柱ABC－A1B1C1底面为正三角形，侧棱与底面垂直，若AB＝2，AA1＝1，则点A到平面A1BC的距离为(B)A．B．C．D．[解析]如图建立空间直角坐标系，则AA1＝(0,0,1)，A1B＝(，1，－1)，A1C＝(0,2，－1)，设平面A1BC的法向量为n＝(x，y，z)，则不妨取z＝2，则x＝，y＝1，∴n＝(，1,2)，∴A到平面A1BC的距离d＝＝.故选B.7．(2019·河南安阳)二面角的棱上有A，B两点，直线AC，BD分别在这个二面角的两个半平面内，且都垂直于AB.已知AB＝4，AC＝6，BD＝8，CD＝2，则该二面角的大小为(C)A．150°B．45°C．60°D．120°[解析]二面角的大小为AC，BD， DC＝AC－AB－BD，两边平方得68＝36＋16＋64－96cosAC，BD，∴cosAC，BD＝，∴AC，BD＝60°，故选C.二、多选题8．已知空间中两条直线a，b所成的角为50°，P为空间中给定的一个定点，直线l过点P且与直线a和直线b所成的角都是θ(0°<θ≤90°)，则下列选项正确的是(ABCD)A．当θ＝15°时，满足题意的直线l不存在B．当θ＝25°时，满足题意的直线l有且仅有1条C．当θ＝40°时，满足题意的直线l有且仅有2条D．当θ＝65°时，满足题意的直线l有且仅有3条[解析]过点P分别作a′∥a，b′∥b，则a′与b′所成的角为50°，由题意可知25°≤θ≤90°，∴当θ＝15°时，满足题意的直线不存在，故A正确；当θ＝25°时，直线l过点P且与a′，b′在同一平面内，且平分a′与b′所成角，∴满足题意的直线有且仅有1条；故B正确；当25°<θ<65°时，满足题意的直线l有且仅有2条，故C正确；当θ＝65°时，满足题意的直线有且仅有3条，故D正确．9．(2020·山东济南期末)给定两个不共线的空间向量a与b，定义叉乘运算；a×b.规定：①a×b为同时与a，b垂直的向量；②a，b，a×b三个向量构成右手系(如图1)；③|a×b|＝|a||b|sin〈a，b〉．如图2，在长方体ABCD－A1B1C1D1中，AB＝AD＝2，AA1＝4，则下列结论正确的是(ACD)A．AB×AD＝AA1B.AB×AD＝AD×ABC．(AB＋AD)×AA1＝AB×AA1＋AD×AA1D．长方体ABCD－A1B1C1D1的体积V＝(AB×AD)·CC1[解析]由叉乘运算定义知A正确；AB×AD＝－AD×AB，B...