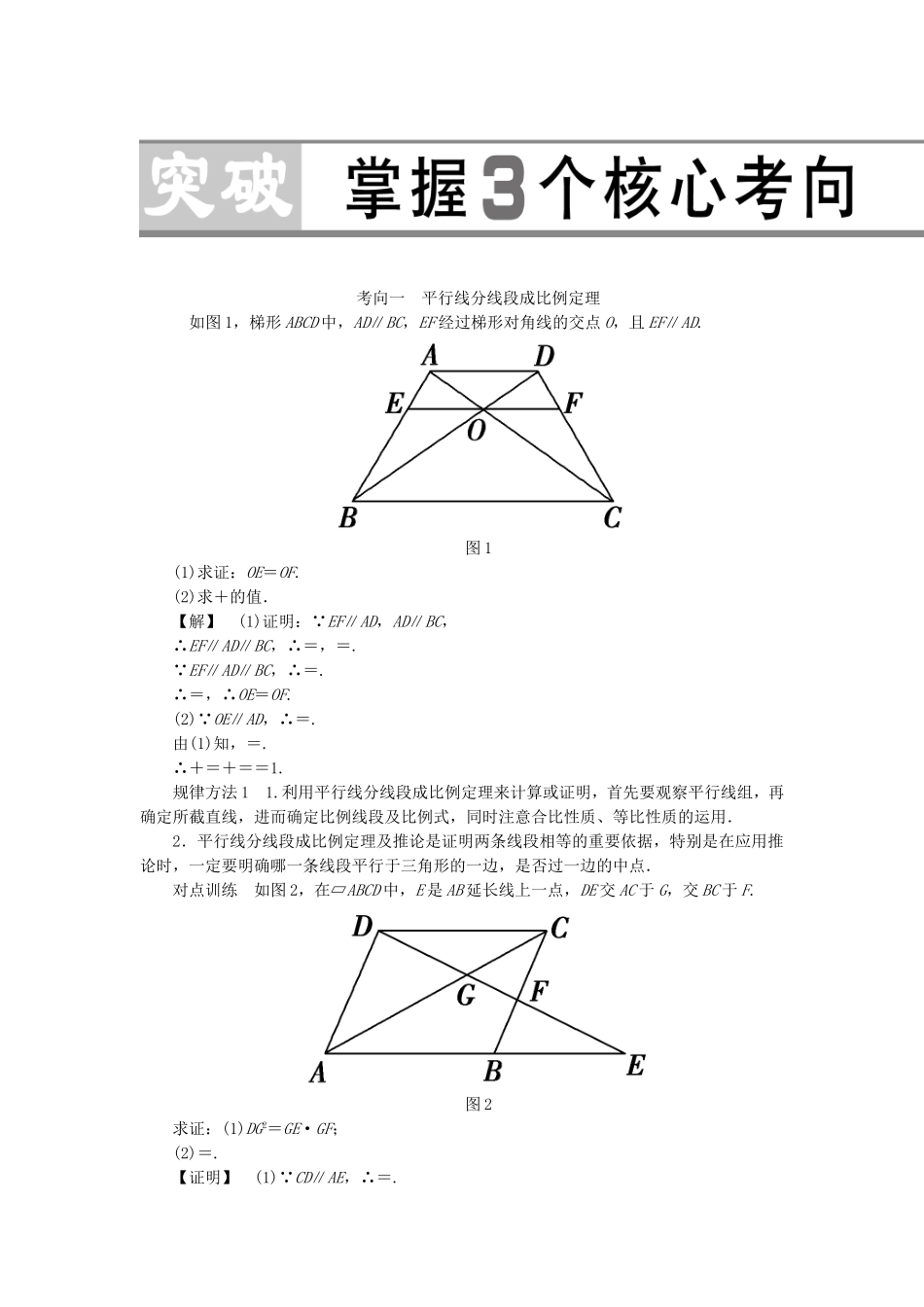
选修4-1几何证明选讲第一节相似三角形的判定及有关性质[考情展望]1.理解相似三角形的定义与性质,了解平行截割定理.2.会证明和应用直角三角形射影定理.1.平行线等分线段定理(1)定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.(2)推论1:经过三角形一边的中点与另一边平行的直线必平分第三边.(3)推论2:经过梯形一腰的中点,且与底边平行的直线平分另一腰.2.平行线分线段成比例定理(1)定理:三条平行线截两条直线,所得的对应线段成比例.(2)推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.3.相似三角形的判定(1)定义:对应角相等,对应边成比例的两个三角形叫做相似三角形.(2)预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.(3)判定定理1:两角对应相等,两三角形相似.定理2:两边对应成比例且夹角相等,两三角形相似.定理3:三边对应成比例,两三角形相似.4.相似三角形的性质(1)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.(2)相似三角形周长的比等于相似比.(3)相似三角形面积的比等于相似比的平方.(4)相似三角形外接圆的直径比、周长比等于相似比,外接圆的面积比等于相似比的平方.5.直角三角形的射影定理直角三角形斜边上的高是两直角边在斜边上的射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项.考向一平行线分线段成比例定理如图1,梯形ABCD中,AD∥BC,EF经过梯形对角线的交点O,且EF∥AD.图1(1)求证:OE=OF.(2)求+的值.【解】(1)证明: EF∥AD,AD∥BC,∴EF∥AD∥BC,∴=,=. EF∥AD∥BC,∴=.∴=,∴OE=OF.(2) OE∥AD,∴=.由(1)知,=.∴+=+==1.规律方法11.利用平行线分线段成比例定理来计算或证明,首先要观察平行线组,再确定所截直线,进而确定比例线段及比例式,同时注意合比性质、等比性质的运用.2.平行线分线段成比例定理及推论是证明两条线段相等的重要依据,特别是在应用推论时,一定要明确哪一条线段平行于三角形的一边,是否过一边的中点.对点训练如图2,在▱ABCD中,E是AB延长线上一点,DE交AC于G,交BC于F.图2求证:(1)DG2=GE·GF;(2)=.【证明】(1) CD∥AE,∴=.又 AD∥CF,∴=.∴=,即DG2=GE·GF.(2) BF∥AD,∴=.又 CD∥BE,∴=.∴=.考向二相似三角形的判定与性质(2015·开封模拟)如图3,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE,F为AE上一点,且∠BFE=∠C.图3(1)求证:△ABF∽△EAD;(2)若AB=4,∠BAE=30°,AD=3,求BF的长.【解】(1)证明: AB∥CD,∴∠BAF=∠AED.又 ∠BFE=∠C,∠BFE+∠BFA=∠C+∠EDA,∴∠BFA=∠ADE.∴△ABF∽△EAD.(2) ∠BAE=30°,∴∠AEB=60°,∴=sin60°,AE==,又=,∴BF=·AD=.规律方法21.相似三角形的证明方法:(1)先找两对内角对应相等;(2)若只有一个角对应相等,再判定这个角的两邻边是否对应成比例;(3)若无角对应相等,就要证明三边对应成比例.2.利用相似三角形的性质进行对应边的比、对应角的度数的相关运算时,要善于联想变换比例式,通过添加辅助线构造相似三角形,同时注意面积法的应用.对点训练如图4,在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC的延长线于点D.图4(1)求证:=;(2)若AC=3,求AP·AD的值.【解】(1)证明:因为∠CPD=∠ABC,∠PDC=∠PDC,所以△DPC∽△DBA,所以=.又AB=AC,所以=.(2)因为∠ABC+∠APC=180°,∠ACB+∠ACD=180°,∠ABC=∠ACB,所以∠ACD=∠APC.又∠CAP=∠DAC,所以△APC∽△ACD,所以=.所以AP·AD=AC2=9.考向三直角三角形的射影定理及其应用如图5,Rt△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AC于E,EF⊥BC于F.求证:EF∶DF=BC∶AC.图5【解】 ∠BAC=90°,且AD⊥BC,∴由射影定理得AC2=CD·BC,∴=.① EF⊥BC,AD⊥BC,∴EF∥AD,∴=.又BE平分∠ABC,且EA⊥AB,EF⊥BC,∴AE=EF,∴=.②由①②得=,即EF∶DF=BC∶AC.规律方法3已知条件中含直角三角形且涉及直角三角形斜边...