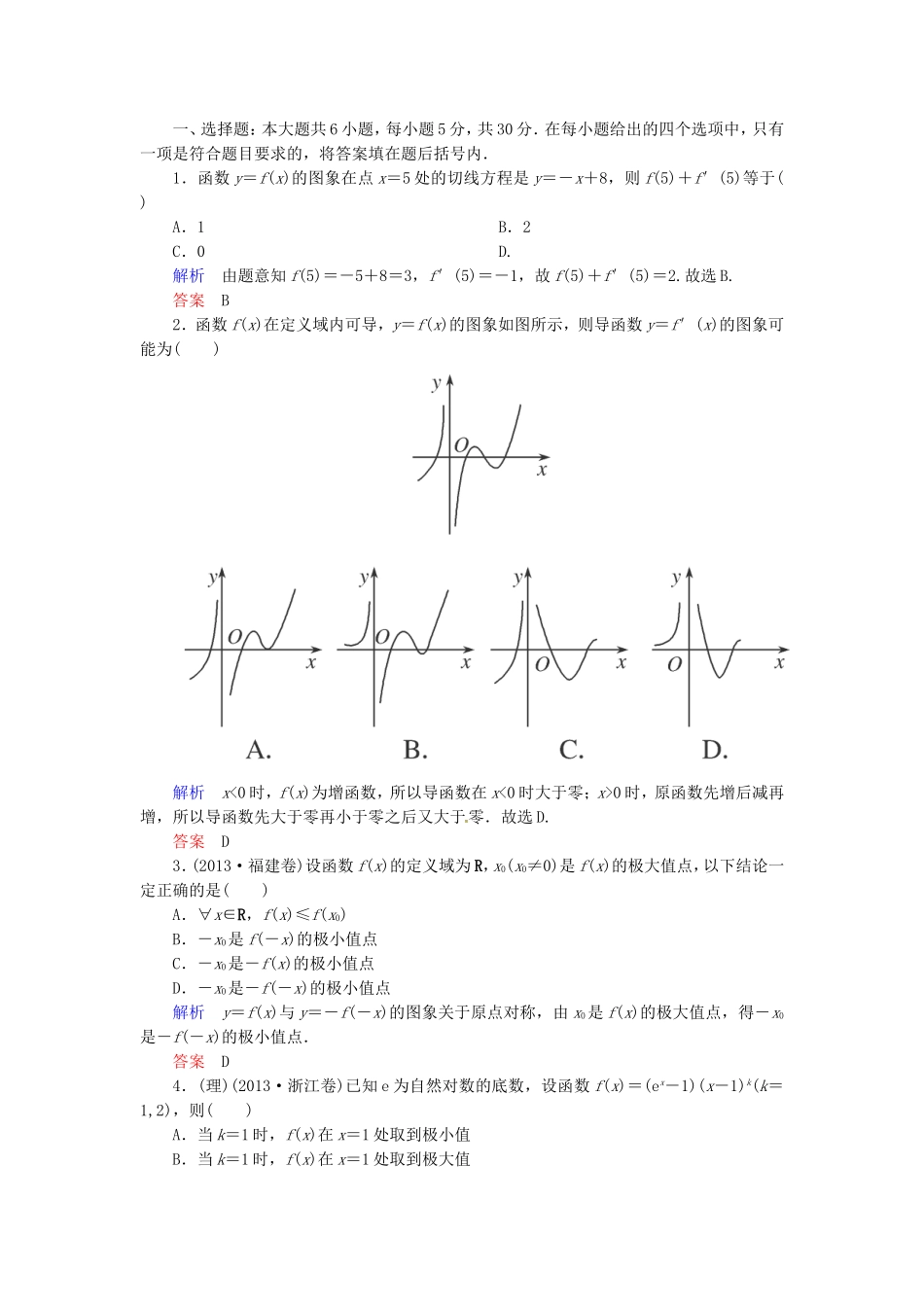
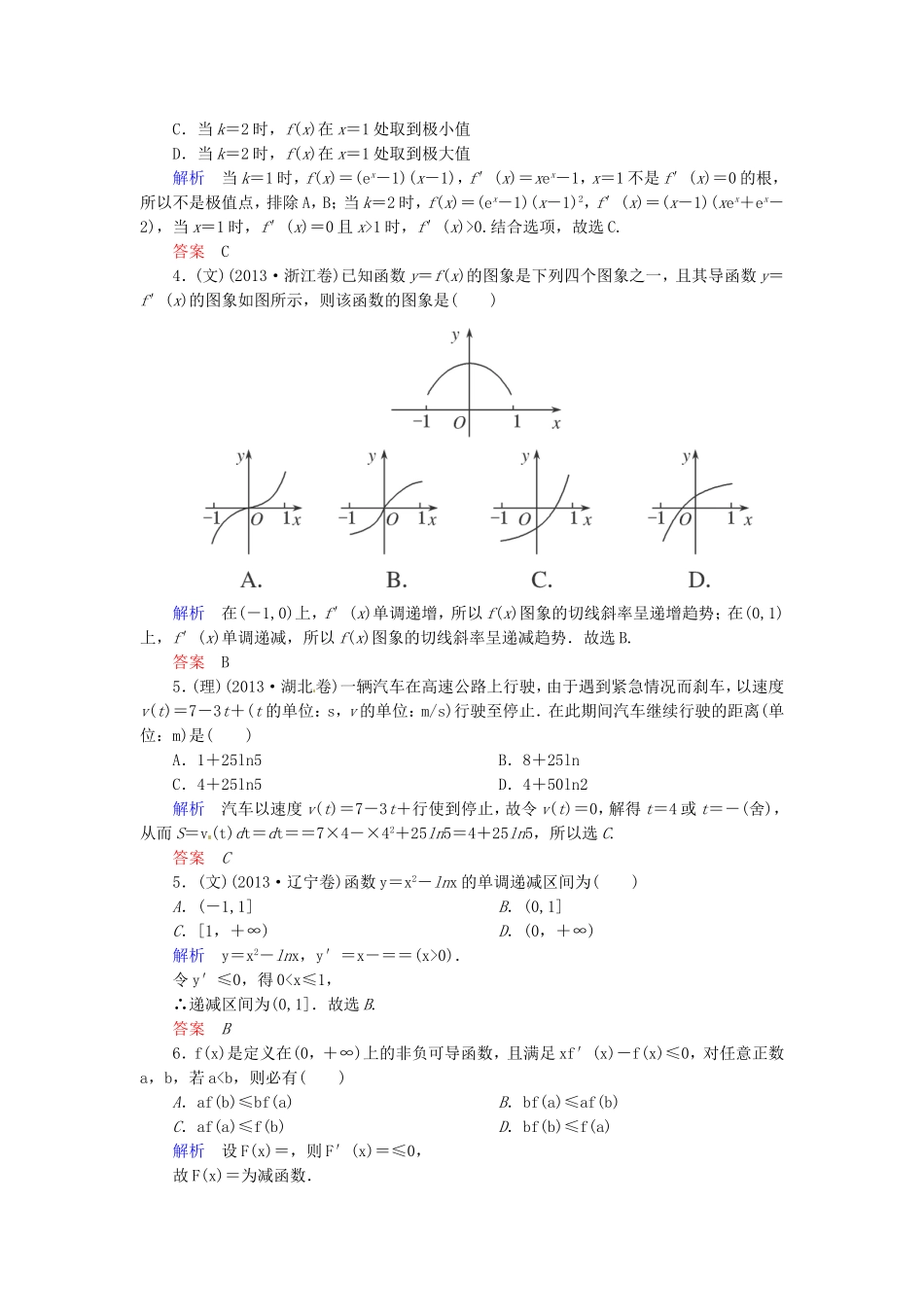
一、选择题:本大题共6小题,每小题5分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,将答案填在题后括号内.1.函数y=f(x)的图象在点x=5处的切线方程是y=-x+8,则f(5)+f′(5)等于()A.1B.2C.0D.解析由题意知f(5)=-5+8=3,f′(5)=-1,故f(5)+f′(5)=2.故选B.答案B2.函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能为()解析x<0时,f(x)为增函数,所以导函数在x<0时大于零;x>0时,原函数先增后减再增,所以导函数先大于零再小于零之后又大于零.故选D.答案D3.(2013·福建卷)设函数f(x)的定义域为R,x0(x0≠0)是f(x)的极大值点,以下结论一定正确的是()A.∀x∈R,f(x)≤f(x0)B.-x0是f(-x)的极小值点C.-x0是-f(x)的极小值点D.-x0是-f(-x)的极小值点解析y=f(x)与y=-f(-x)的图象关于原点对称,由x0是f(x)的极大值点,得-x0是-f(-x)的极小值点.答案D4.(理)(2013·浙江卷)已知e为自然对数的底数,设函数f(x)=(ex-1)(x-1)k(k=1,2),则()A.当k=1时,f(x)在x=1处取到极小值B.当k=1时,f(x)在x=1处取到极大值C.当k=2时,f(x)在x=1处取到极小值D.当k=2时,f(x)在x=1处取到极大值解析当k=1时,f(x)=(ex-1)(x-1),f′(x)=xex-1,x=1不是f′(x)=0的根,所以不是极值点,排除A,B;当k=2时,f(x)=(ex-1)(x-1)2,f′(x)=(x-1)(xex+ex-2),当x=1时,f′(x)=0且x>1时,f′(x)>0.结合选项,故选C.答案C4.(文)(2013·浙江卷)已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象是()解析在(-1,0)上,f′(x)单调递增,所以f(x)图象的切线斜率呈递增趋势;在(0,1)上,f′(x)单调递减,所以f(x)图象的切线斜率呈递减趋势.故选B.答案B5.(理)(2013·湖北卷)一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度v(t)=7-3t+(t的单位:s,v的单位:m/s)行驶至停止.在此期间汽车继续行驶的距离(单位:m)是()A.1+25ln5B.8+25lnC.4+25ln5D.4+50ln2解析汽车以速度v(t)=7-3t+行使到停止,故令v(t)=0,解得t=4或t=-(舍),从而S=v(t)dt=dt==7×4-×42+25ln5=4+25ln5,所以选C.答案C5.(文)(2013·辽宁卷)函数y=x2-lnx的单调递减区间为()A.(-1,1]B.(0,1]C.[1,+∞)D.(0,+∞)解析y=x2-lnx,y′=x-==(x>0).令y′≤0,得0
0,f(t)=lnt+t,即f(x)=x+lnx(x>0),f′(x)=1+,于是f′(1)=2.答案28.函数f(x)=x3-3a2x+a(a>0)的极大值是正数,极小值是负数,则a的取值范围是________.解析f′(x)=3x2-3a2=3(x+a)(x-a),由f′(x)=0得x=±a,当-aa或x<-a时,f′(x)>0,函数递增,∴f(-a)=-a3+3a3+a>0,且f(a)=a3-3a3+a<0,解得a>.答案9.若点P是曲线y=x2-lnx上任意一点,则点P到直线y=x-2的最小距离为________.解析过点P作y=x-2的平行直线,且与曲线y=x2-lnx相切.设P(x0,x-lnx0),则有k=y′|x=x0=2x0-.∴2x0-=1.∴x0=1或x0=-(舍去).∴P(1,1),∴d==.答案三、解答题:本大题共3小题,共30分.解答应写出文字说明、证明过程或演算步骤.10.(本小题10分)已知函数f(x)=4x3+3tx2-6t2x+t-1,x∈R,其中t∈R.(1)当t=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;(2)t≠0时,求f(x)的单调区间.解(1)当t=1时,f(x)=4x3+3x2-6x,f(0)=0,f′(x)=12x2+6x-6,f′(0)=-6,所以曲线y=f(x)在点(0,f(0))处的切线方程为y=-6x.(2)f′(x)...