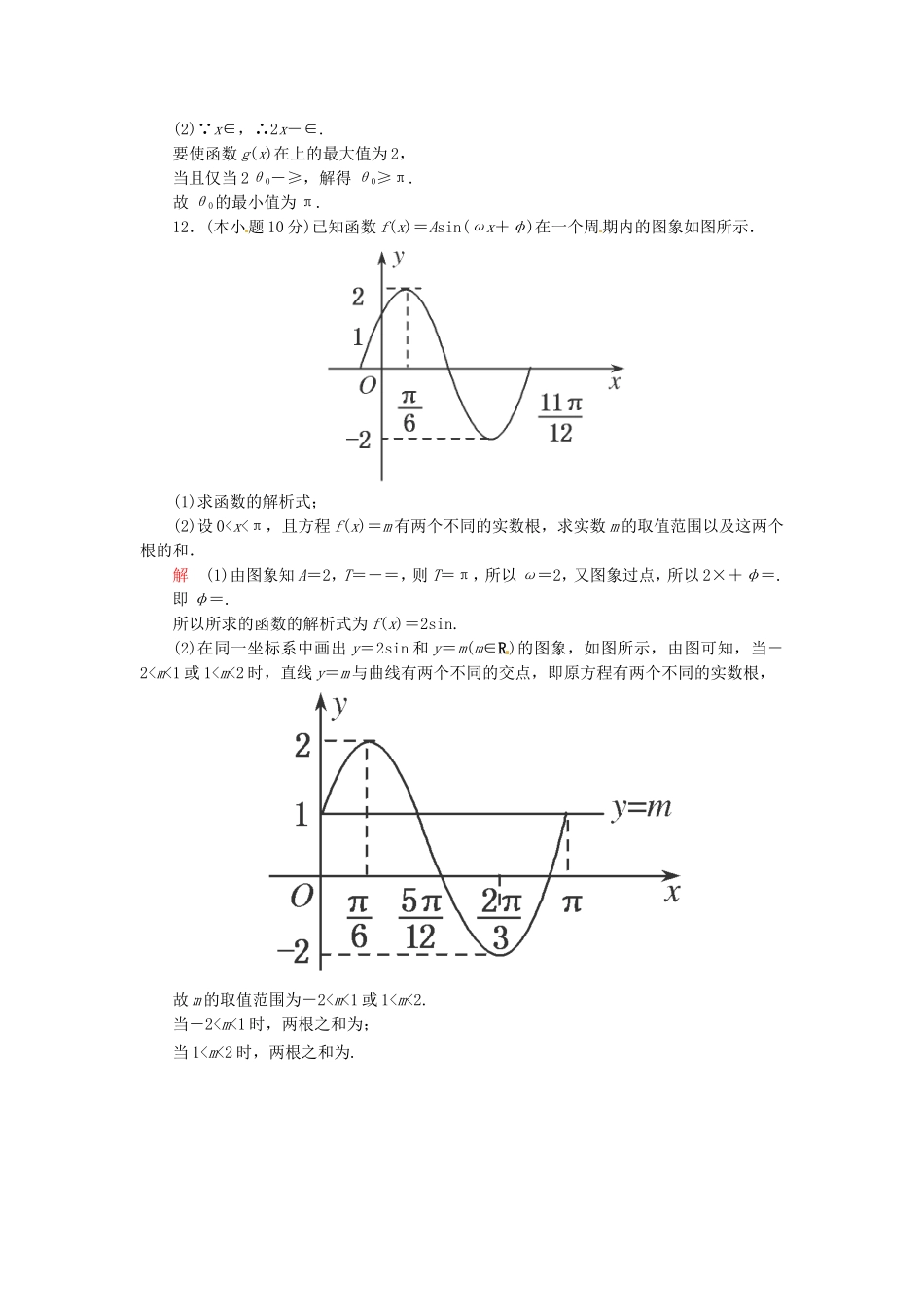
一、选择题:本大题共6小题,每小题5分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,将答案填在题后括号内.1.已知sinα=,α∈,则cos(π-α)等于()A.-B.-C.D.解析∵sinα=,α∈,∴cosα=-.∴cos(π-α)=-cosα=,故选D.答案D2.将函数y=cos2x的图象向右平移个单位,得到函数y=f(x)·sinx的图象,则f(x)的表达式可以是()A.f(x)=-2cosxB.f(x)=2cosxC.f(x)=sin2xD.f(x)=(sin2x+cos2x)解析函数y=cos2x的图象向右平移个单位后得到y=cos=cos=sin2x=2sinxcosx.故f(x)可以为2cosx.选B.答案B3.下列函数中周期为π且为偶函数的是()A.y=sinB.y=cosC.y=sinD.y=cos解析由周期为π知ω=2,排除C、D.由诱导公式知,A选项中,得y=-cos2x,为偶函数.答案A4.把函数y=sin图象上各点的横坐标缩短到原来的(纵坐标不变),再将图象向右平移个单位,那么所得图象的一条对称轴方程为()A.x=-B.x=-C.x=D.x=解析y=sin图象上各点的横坐标缩短到原来的(纵坐标不变),得到函数y=sin的图象,再将图象向右平移个单位,得到函数y=sin=sin的图象,x=-是其图象的一条对称轴方程.答案A5.(2013·山东卷)将函数y=sin(2x+φ)的图象沿x轴向左平移个单位后,得到一个偶函数的图象,则φ的一个可能取值为()A.B.C.0D.-解析y=sin(2x+φ)向左平移个单位后得图象的解析式为y=sin为偶函数,故+φ=+kπ(k∈Z),φ=+kπ(k∈Z).答案B6.(2013·安徽黄山高三联考)设函数f(x)=cos(2x+φ)+sin(2x+φ),且其图象关于直线x=0对称,则()A.y=f(x)的最小正周期为π,且在上为增函数B.y=f(x)的最小正周期为π,且在上为减函数C.y=f(x)的最小正周期为,且在上为增函数D.y=f(x)的最小正周期为,且在上为减函数解析f(x)=cos(2x+φ)+sin(2x+φ)=2sin,∵其图象关于x=0对称,∴f(x)是偶函数.∴+φ=+kπ,k∈Z.又∵|φ|<,∴φ=.∴f(x)=2sin=2cos2x.易知f(x)的最小正周期为π,在上为减函数.答案B二、填空题:本大题共3小题,每小题5分,共15分.将答案填在题中横线上.7.若=2,则sin(θ-5π)sin=________.解析由已知得=2,∴tanθ=3.∴sin(θ-5π)·sin=sinθcosθ===.答案8.(2013·江西卷)函数y=sin2x+2sin2x的最小正周期T为________.解析y=sin2x+2sin2x=sin2x-cos2x+=2sin+,所以周期T==π.答案π9.函数y=sin(ωx+φ)在区间上单调递减,且函数值从1减小到-1,那么此函数图象与y轴交点的纵坐标为________.解析因为函数的最大值为1,最小值为-1,且在区间上单调递减,又函数值从1减小到-1,可知-=为半周期,则周期为π,ω===2,此时原式为y=sin(2x+φ),又由函数过点,代入可得φ=,因此函数y=sin,令x=0,可得y=.答案三、解答题:本大题共3小题,共30分.解答应写出文字说明、证明过程或演算步骤.10.(本小题10分)(2013·天津卷)已知函数f(x)=-sin+6sinxcosx-2cos2x+1,x∈R.(1)求f(x)的最小正周期;(2)求f(x)在区间上的最大值和最小值.解(1)f(x)=-sin2x·cos-cos2x·sin+3sin2x-cos2x=2sin2x-2cos2x=2sin.所以f(x)的最小正周期T==π.(2)因为f(x)在区间上是增函数,在区间上是减函数,又f(0)=-2,f=2,f=2,故函数f(x)在区间上的最大值为2,最小值为-2.11.(本小题10分)(2013·安徽江南十校)将函数y=sinx的图象向右平移个单位,再将所得的图象上各点的横坐标不变,纵坐标伸长到原来的4倍.这样得到函数f(x)的图象.若g(x)=f(x)cosx+.(1)将函数g(x)化成g(x)=Asin(ωx+φ)+B的形式;(2)若函数g(x)在区间上的最大值为2,试求θ0的最小值.解(1)由题意可得f(x)=4sin,∴g(x)=4sincosx+=4cosx+=2(sinxcosx-cos2x)+=2sin.(2)∵x∈,∴2x-∈.要使函数g(x)在上的最大值为2,当且仅当2θ0-≥,解得θ0≥π.故θ0的最小值为π.12.(本小题10分)已知函数f(x)=Asin(ωx+φ)在一个周期内的图象如图所示.(1)求函数的解析式;(2)设0