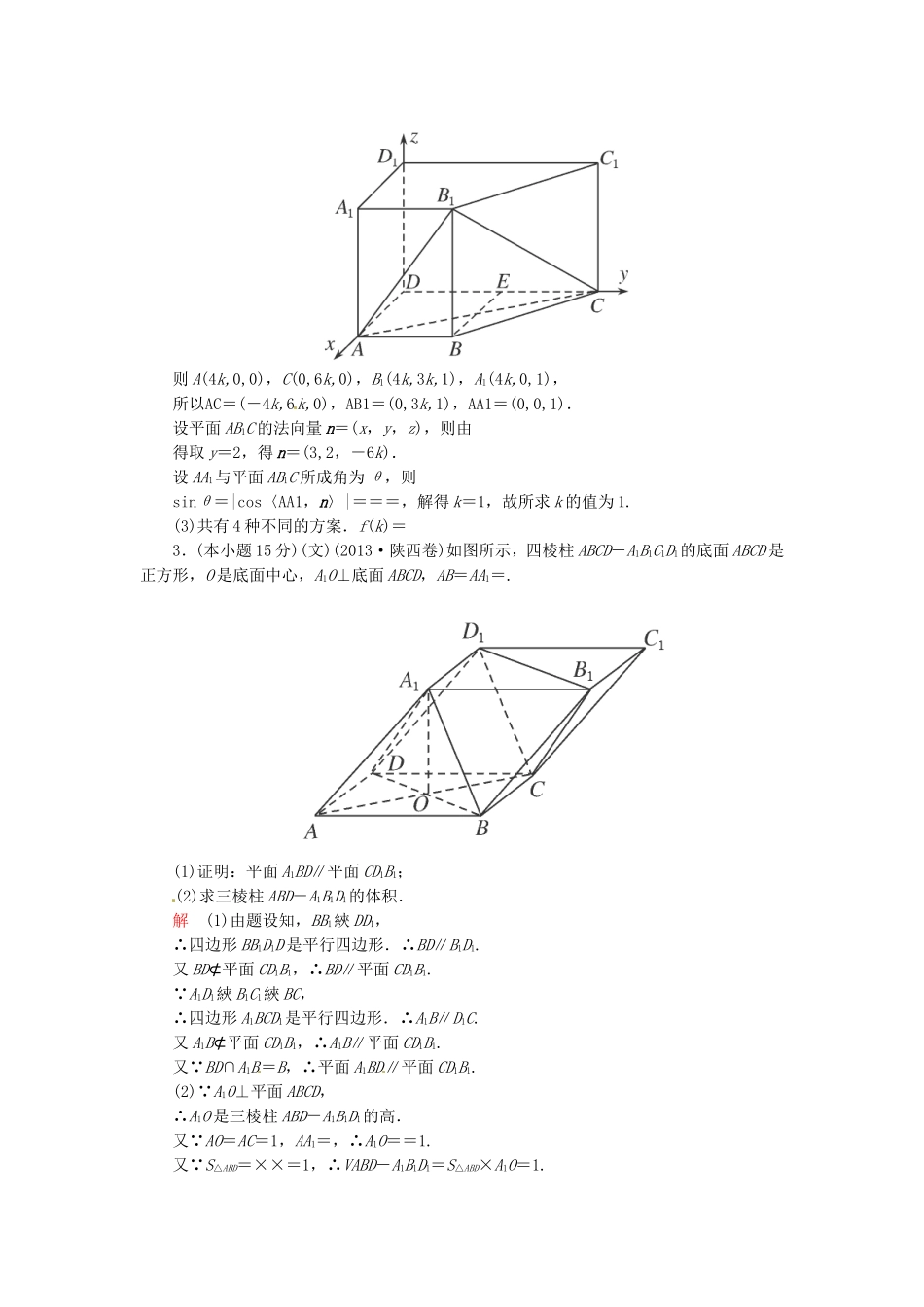
1.(本小题15分)(2013·山东淄博一模)已知向量m=,n=(1,2sinB),m·n=sin2C,其中A,B,C分别为△ABC的三边a,b,c所对的角.(1)求角C的大小;(2)若sinA+sinB=2sinC,且S△ABC=,求边c的长.解(1) m·n=sin(A-B)+2cosAsinB=sinAcosB+cosAcosB=sin(A+B),在△ABC中,A+B=π-C且00,得ω=2.又f(x)过点,∴sin+=1,得cosφ=.又 0<φ<,∴φ=.∴f(x)=sin+.(2) f=,得:sinC+=,∴sinC=. 角C为锐角,∴cosC=.又 a=,S△ABC=absinC=··b·=2,∴b=6.由余弦定理:c2=a2+b2-2abcosC=5+36-2··6·=21,∴c=.3.(本小题15分)(理)(2013·福建卷)如图所示,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).(1)求证:CD⊥平面ADD1A1;(2)若直线AA1与平面AB1C所成角的正弦值为,求k的值;(3)现将与四棱柱ABCD-A1B1C1D1形状和大小完全相同的两个四棱柱拼接成一个新的四棱柱.规定:若拼接成的新四棱柱形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为f(k),写出f(k)的解析式.(直接写出答案,不必说明理由)解(1)取CD的中点E,连接BE. AB∥DE,AB=DE=3k,∴四边形ABED为平行四边形.∴BE∥AD且BE=AD=4k.在△BCE中, BE=4k,CE=3k,BC=5k,∴BE2+CE2=BC2.∴∠BEC=90°,即BE⊥CD.又BE∥AD,∴CD⊥AD. AA1⊥平面ABCD,CD⊂平面ABCD,∴AA1⊥CD.又AA1∩AD=A,∴CD⊥平面ADD1A1.(2)以D为原点,DA,DC,DD1的方向为x,y,z轴的正方向建立如图所示的空间直角坐标系,则A(4k,0,0),C(0,6k,0),B1(4k,3k,1),A1(4k,0,1),所以AC=(-4k,6k,0),AB1=(0,3k,1),AA1=(0,0,1).设平面AB1C的法向量n=(x,y,z),则由得取y=2,得n=(3,2,-6k).设AA1与平面AB1C所成角为θ,则sinθ=|cos〈AA1,n〉|===,解得k=1,故所求k的值为1.(3)共有4种不同的方案.f(k)=3.(本小题15分)(文)(2013·陕西卷)如图所示,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=.(1)证明:平面A1BD∥平面CD1B1;(2)求三棱柱ABD-A1B1D1的体积.解(1)由题设知,BB1綊DD1,∴四边形BB1D1D是平行四边形.∴BD∥B1D1.又BD⊄平面CD1B1,∴BD∥平面CD1B1. A1D1綊B1C1綊BC,∴四边形A1BCD1是平行四边形.∴A1B∥D1C.又A1B⊄平面CD1B1,∴A1B∥平面CD1B1.又 BD∩A1B=B,∴平面A1BD∥平面CD1B1.(2) A1O⊥平面ABCD,∴A1O是三棱柱ABD-A1B1D1的高.又 AO=AC=1,AA1=,∴A1O==1.又 S△ABD=××=1,∴VABD-A1B1D1=S△ABD×A1O=1.4.(本小题15分)(理)(2013·重庆卷)某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球,再从装有1个蓝球与2个白球的袋中任意摸出1个球.根据摸出4个球中红球与蓝球的个数,设一、二、三等奖如下:奖级摸出红、蓝球个数获奖金额一等奖3红1蓝200元二等奖3红0蓝50元三等奖2红1蓝10元其余情况无奖且每次摸奖最多只能获得一个奖级.(1)求一次摸奖恰好摸到1个红球的概率;(2)求摸奖者在一次摸奖中获奖金额X的分布列与期望E(X).解设Ai表示摸到i个红球,Bj表示摸到j个蓝球,则Ai(i=0,1,2,3)与Bj(j=0,1)独立.(1)恰好摸到1个红球的概率为P(A1)==.(2)X的所有可能值为:0,10,50,200,且P(X=200)=P(A3B1)=P(A3)P(B1)=·...