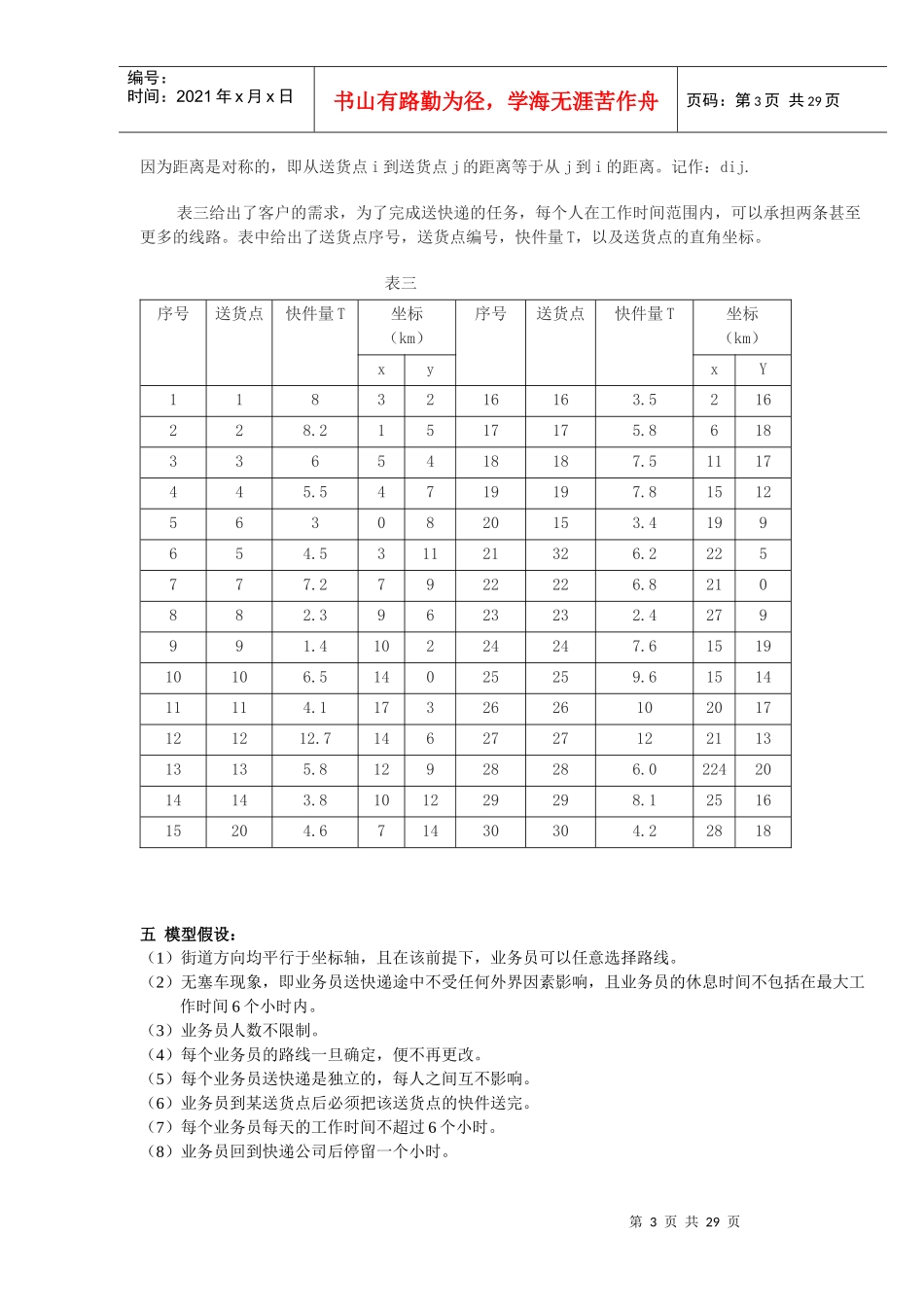
第1页共29页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第1页共29页快递公司送货策略一摘要:本文是关于快递公司送货策略的优化设计问题,即在给定送货地点和给定设计规范的条件下,确定所需业务员人数,每个业务员的运行线路,总的运行公里数,以及费用最省的策略。本文主要从最短路经和费用最省两个角度解决该问题,建立了两个数据模型。模型一:利用“图”的知识,将送货点抽象为“图”中是顶点,由于街道和坐标轴平行,即任意两顶点之间都有路。在此模型中,将两点之间的路线权值赋为这两点横纵坐标之和。如A(x1,y1),B(x2,y2)两点,则权值为D=|x2-x1|+|y2-y1|。并利用计算机程序对以上结果进行了校核。模型二:根据题意,建立动态规划的数学模型。然后用动态规划的知识求得最优化结果。根据所建立的两个数学模型,对满足设计要求的送货策略和费用最省策略进行了模拟,在有标尺的坐标系中得到了能够反映运送最佳路线的模拟图。最后,对设计规范的合理性进行了充分和必要的论证。二关键词:快递公司送货最优化图模型多目标动态规划TSP模型三问题重述:在快递公司送货策略中,确定业务员人数和各自的行走路线是本题的关键。这个问题可以描述为:一中心仓库(或配送调度中心)拥有最大负重为25kg的业务员m人,负责对30个客户进行货物分送工作,客户i的快件量为已知,求满足需求的路程最短的人员行驶路径,且使用尽量少的人数,并满足以下条件:1)每条送快件的路径上各个客户的需求量之和不超过个人最大负重。2)每个客户的需求必须满足,且只能由一个人送货.3)每个业务员每天平均工作时间不超过6小时,在每个送货点停留的时间为10分钟,途中速度为25km/h。4)为了计算方便,我们将快件一律用重量来衡量,平均每天收到总重量为184.5千克。表一为题中所给的数据:表一最大载重量25kg重载时速20km/h途中的平均速度25km/h重载酬金3元/km*kg业务员工作时间上限6h空载时速30km/h每个送货点停留时间10min空载酬金2元/km备注1、快件一律用重量来衡量2、假定街道方向均平行于坐标轴第2页共29页第1页共29页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第2页共29页处于实际情况的考虑,本研究中对人的最大行程不加限制.本论文试图从最优化的角度,建立起满足设计要求的送货的数学模型,借助于计算机的高速运算与逻辑判断能力,求出满足题意要求的结果。四问题分析:从公司总部配出一个人,到任意未配送的送货点,然后将这个人配到最近的未服务的送货点范围之内的邻居,并使送货时间小于6小时,各送货点总重量不超过25kg。继续上述指派,直到各点总重量超过25kg,或者送货时间大于6小时。最后业务员返回总部,记录得到的可行行程(即路线)。对另一个业务员重复上述安排,直到没有未服务的送货点。对得到的可行的行程安排解中的每一条路径,求解一个旅行商问题,决定访问指派给每一条行程的业务员的顺序,最小化运输总距离。得到可行解的行程安排解后退出。根据题意的要求,每个人的工作时间不超过6小时,且必须从早上9点钟开始派送,到当天17点之前(即在8小时之内)派送完毕。且⌈184.5kg25kg⌉=8,故至少需要8条路线。表二列出了题中任意两配送点间的距离。表二:任意两点间的距离矩阵第3页共29页第2页共29页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第3页共29页因为距离是对称的,即从送货点i到送货点j的距离等于从j到i的距离。记作:dij.表三给出了客户的需求,为了完成送快递的任务,每个人在工作时间范围内,可以承担两条甚至更多的线路。表中给出了送货点序号,送货点编号,快件量T,以及送货点的直角坐标。表三序号送货点快件量T坐标(km)序号送货点快件量T坐标(km)xyxY1183216163.5216228.21517175.86183365418187.51117445.54719197.815125630820153.4199654.531121326.2225777.27922226.8210882.39623232.4279991.410224247.6151910106.514025259.6151411114.11732626102017121212.7146272712211313135.812928286.02242014143.8101229298.1251615204.671430304.22818五模型假设:(1)街道方向均平行于坐标轴,且在该前...