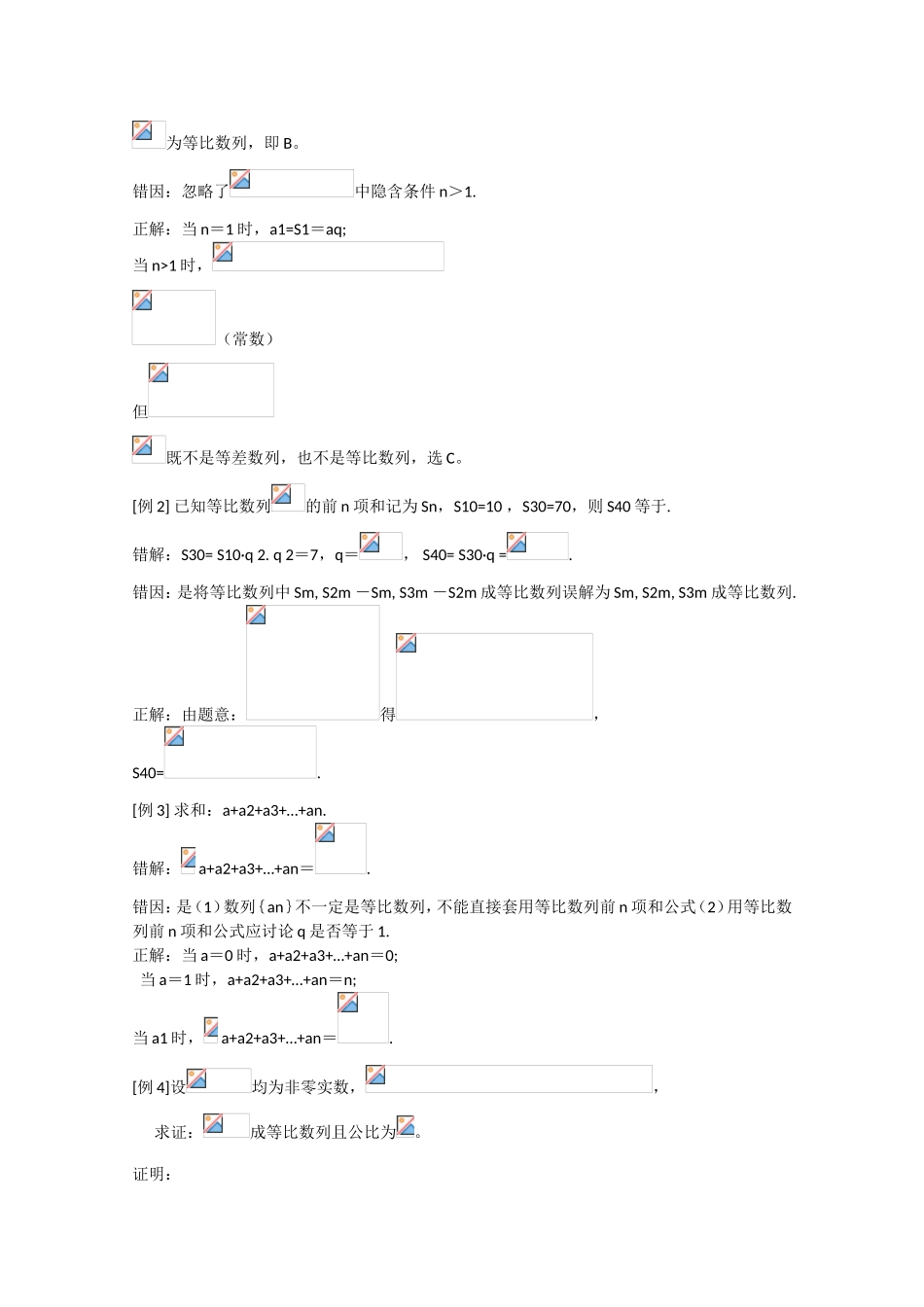
等比数列的通项与求和一、知识导学1.等比数列:一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示.2.等比中项:若a,G,b成等比数列,则称G为a和b的等比中项.3.等比数列的前n项和公式:二、疑难知识导析1.由于等比数列的每一项都可能作分母,故每一项均不为0,因此q也不为0.2.对于公比q,要注意它是每一项与它前一项的比,防止把相邻两项的比的次序颠倒.3.“从第2项起”是因为首项没有“前一项”,同时应注意如果一个数列不是从第2项起,而是从第3项或第4项起每一项与它前一项的比都是同一个常数,此数列不是等比数列,这时可以说此数列从.第2项或第3项起是一个等比数列.4.在已知等比数列的a1和q的前提下,利用通项公式an=a1qn-1,可求出等比数列中的任一项.5.在已知等比数列中任意两项的前提下,使用an=amqn-m可求等比数列中任意一项.6.等比数列{an}的通项公式an=a1qn-1可改写为.当q>0,且q1时,y=qx是一个指数函数,而是一个不为0的常数与指数函数的积,因此等比数列{an}的图象是函数的图象上的一群孤立的点.7.在解决等比数列问题时,如已知,a1,an,d,,n中任意三个,可求其余两个。三、经典例题导讲[例1]已知数列的前n项之和Sn=aqn(为非零常数),则为()。A.等差数列B.等比数列C.既不是等差数列,也不是等比数列D.既是等差数列,又是等比数列错解:(常数)为等比数列,即B。错因:忽略了中隐含条件n>1.正解:当n=1时,a1=S1=aq;当n>1时,(常数)但既不是等差数列,也不是等比数列,选C。[例2]已知等比数列的前n项和记为Sn,S10=10,S30=70,则S40等于.错解:S30=S10·q2.q2=7,q=,S40=S30·q=.错因:是将等比数列中Sm,S2m-Sm,S3m-S2m成等比数列误解为Sm,S2m,S3m成等比数列.正解:由题意:得,S40=.[例3]求和:a+a2+a3+…+an.错解:a+a2+a3+…+an=.错因:是(1)数列{an}不一定是等比数列,不能直接套用等比数列前n项和公式(2)用等比数列前n项和公式应讨论q是否等于1.正解:当a=0时,a+a2+a3+…+an=0;当a=1时,a+a2+a3+…+an=n;当a1时,a+a2+a3+…+an=.[例4]设均为非零实数,,求证:成等比数列且公比为。证明:证法一:关于的二次方程有实根,∴,∴则必有:,即,∴非零实数成等比数列设公比为,则,代入∵,即,即。证法二:∵∴∴,∴,且∵非零,∴。[例5]在等比数列中,,求该数列前7项之积。解:∵,∴前七项之积[例6]求数列前n项和解:①②两式相减:[例7]从盛有质量分数为20%的盐水2kg的容器中倒出1kg盐水,然后加入1kg水,以后每次都倒出1kg盐水,然后再加入1kg水,问:(1)第5次倒出的的1kg盐水中含盐多kg?(2)经6次倒出后,一共倒出多少kg盐?此时加1kg水后容器内盐水的盐的质量分数为多少?解:(1)每次倒出的盐的质量所成的数列为{an},则:a1=0.2(kg),a2=×0.2(kg),a3=()2×0.2(kg)由此可见:an=()n1×0.2(kg),a5=()51×0.2=()4×0.2=0.0125(kg)。(2)由(1)得{an}是等比数列a1=0.2,q=答:第5次倒出的的1kg盐水中含盐0.0125kg;6次倒出后,一共倒出0.39375kg盐,此时加1kg水后容器内盐水的盐的质量分数为0.003125。四、典型习题导练1.求下列各等比数列的通项公式:a1=2,a3=8a1=5,且2an+1=3ana1=5,且2.在等比数列,已知,,求.3.已知无穷数列,求证:(1)这个数列成等比数列(2)这个数列中的任一项是它后面第五项的,(3)这个数列的任意两项的积仍在这个数列中。4.设数列为求此数列前项的和。5.已知数列{an}中,a1=2且an+1=Sn,求an,Sn6.是否存在数列{an},其前项和Sn组成的数列{Sn}也是等比数列,且公比相同?7.在等比数列中,,求的范围。