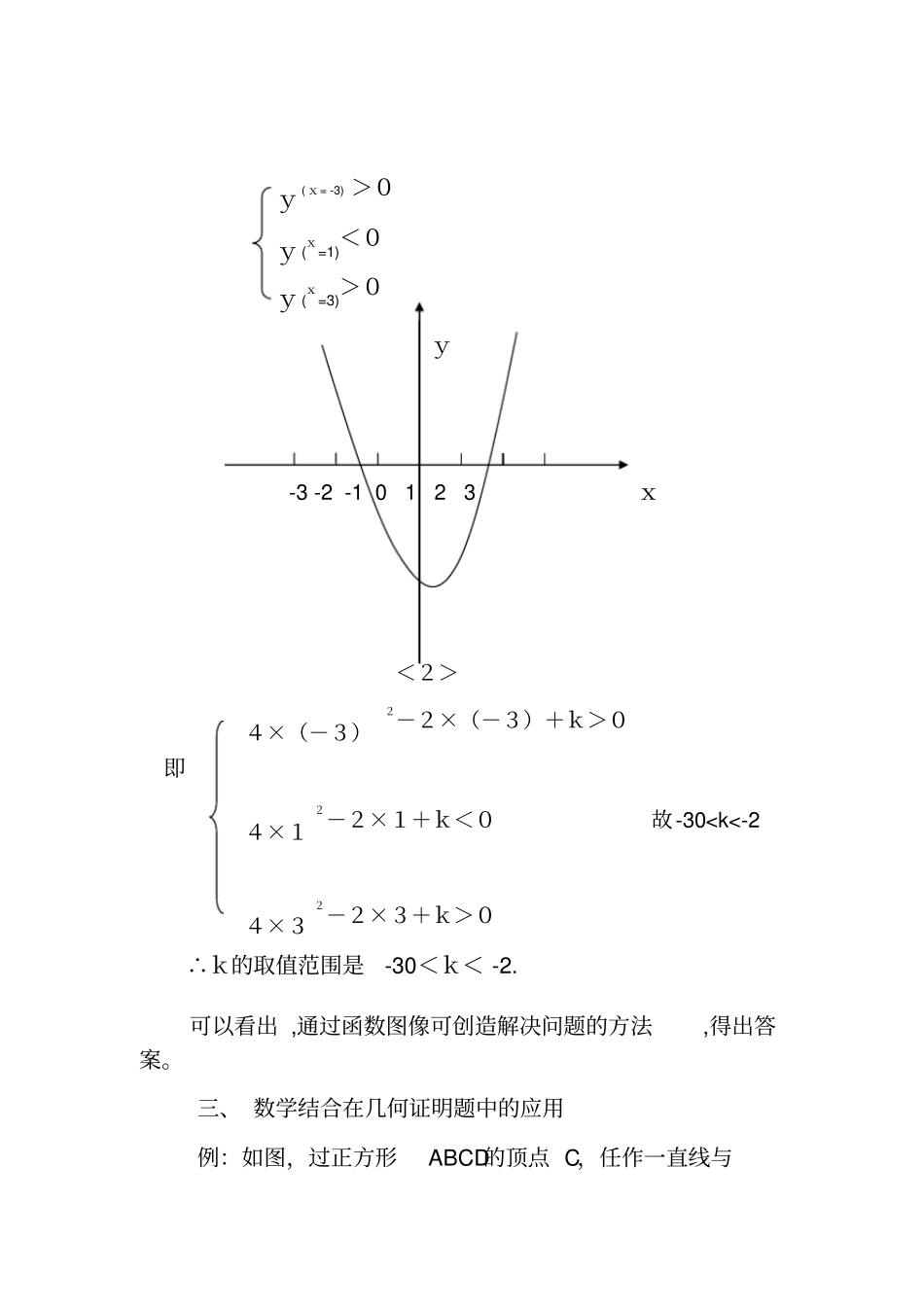
数形结合在初中数学解题教学中的几种应用岚县教研室杨岚锋随着现代科学技术的迅速发展和广泛应用,当代社会对教师的要求也不断提高。要求教师必须有过硬的业务素质和过高的思想政治素质,要掌握广博的科学基础知识和各种基本的操作技能,还要具备适应新科技发展的创造性思维能力和一定的创新精神。因此,要求我们不仅要传授给学生必需的现代科技、现代将设所需要的知识和技能,还必须要培养他们运用知识解决实际问题的能力,特别要培养他们的创造思维能力以及独立获取知识的能力。解题教学不同于概念教学,它是运用基础理论,基本方法求解数学问题的一种教学方法,它综合体现了教师及学生的数学素质,在中学数学教学尤其是在提倡素质教育的今天显得更为重要。解题教学有利于激发学生学习的主动性,增强学习数学的兴趣,感知数学美;有利于培养学生的探索精神、创新精神;有利于培养辩证唯物主义观点。初中数学解题思想及方法颇多,这儿就笔者在平时的教学中总结出的一种“数形结合”解题法做一浅薄的探讨。数形结合是数学中运用广泛但又不易掌握的一种解题思想方法。因为数和形是数学的两大基石,数可准确澄清形的模糊,形能直接启迪数的计算,即以数助形,以形助数。一、数形结合在解绝对值不等式中的应用绝对值的几何意义是:数轴上表示数x的点离开原点的距离,记做︱x︳。那么|x-a|就表示数x的点和数a的点之间的距离。在解绝对值不等式时,若与数轴结合起来,采用数形结合的方法,问题就会变的简单直观。例:不等式|x+2|+|x-3|>5的解集是___解:从数轴上看,-2到3的距离是5,所以x不能在-2和3之间(包括-2和3),x只能在-2的左侧或3的右侧,不等式才能成立,故原不等式的解集是x>3或x<-2。-4-3-2-101234<1>可以看出,通过画数轴图形,可以使复杂问题简单化,开阔解题思路,甚至直接得出绝对值不等式的答案。二、数形结合在解函数题中的应用函数关系与图像是同时存在的,所以在解函数题时,可借助图像灵活、快速解题。例:若方程4x2-2x+k=0的一个根大于-3且小于1,另一个根大于1且小于3,求k的取值范围.解:令y=4x2-2x+k,则其图像如图<2>y(x=-3)>0y(x=1)<0y(x=3)>0y-3-2-10123x<2>4×(-3)2-2×(-3)+k>0即4×12-2×1+k<0故-30