湖北汽车工业学院专升本习题解答(定积分的应用)VIP免费

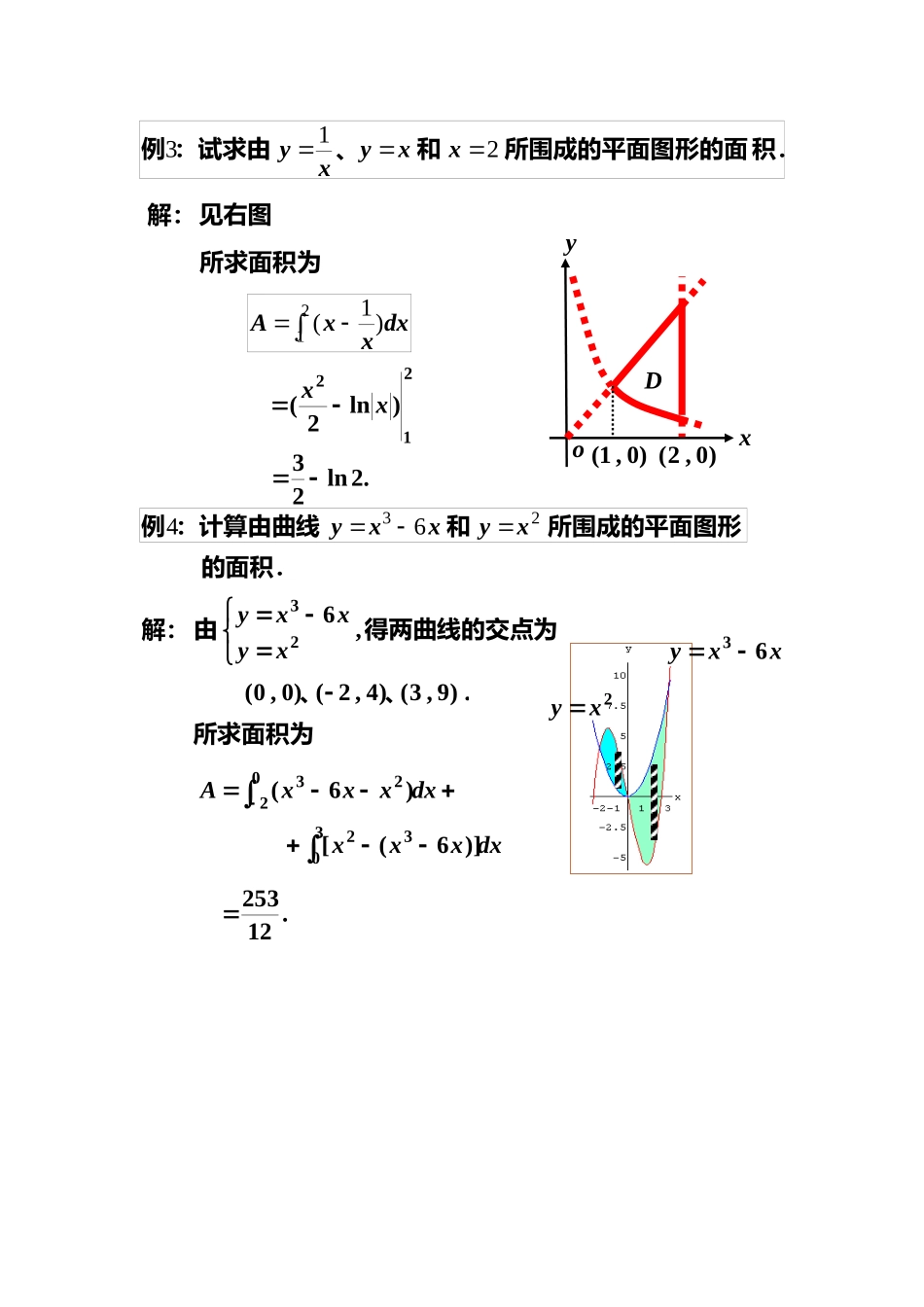
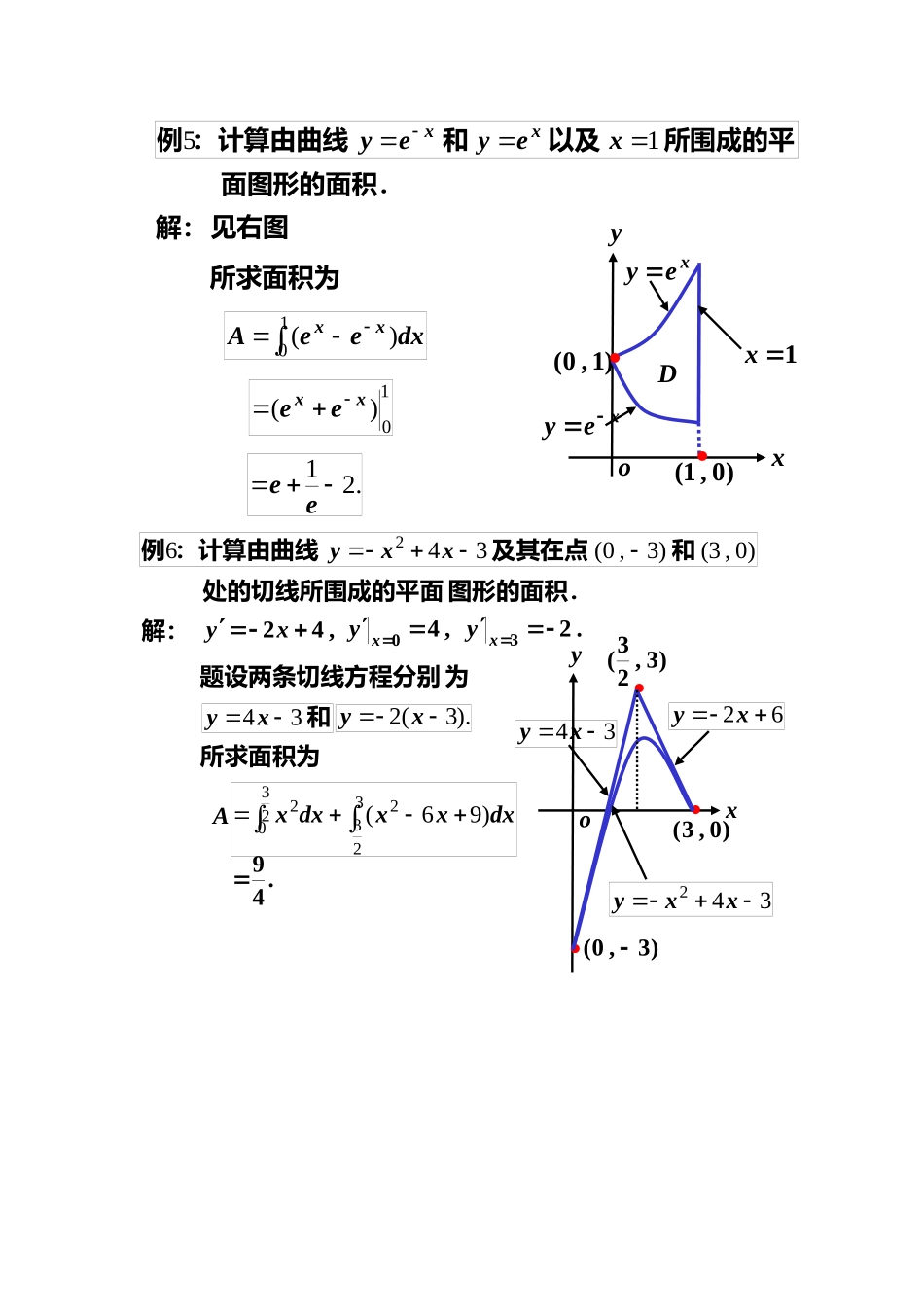
所围成的平面图和：计算由两条抛物线例221xyxy形的面积．解：得两曲线的交点为由,22yxxy．、)1,1()0,0(oxyxy22xy)1,1(D所求面积为102)(dxxxA10323)332(xx.31所围成的平面和直线：试求抛物线例4222xyxy图形的面积．解：得两曲线的交点为由,422xyxy．、)4,8()2,2(oxyxy224xy)2,2()4,8(D422]214[(dyy)yA所求面积为4232)642(-yyy.18积．所围成的平面图形的面和、：试求由例213xxyxy解：见右图oxy)0,1()0,2(D所求面积为21)1(dxxxA212)ln2(xx.2ln23所围成的平面图形和：计算由曲线例2364xyxxy的面积．解：得两曲线的交点为由,623xyxxy．、、)9,3()4,2()0,0(2xyxxy63dxxxxA0223)6(dxxxx3032)]6([.12253所求面积为所围成的平以及和：计算由曲线例15xeyeyxx面图形的面积．解：见右图oxy)1,0(·)0,1(·D所求面积为10)(dxeeAxx10)(xxee.21eexeyxey1x)3,0()0,3()3,0(3462和及其在点：计算由曲线例xxy图形的面积．处的切线所围成的平面解：,42xy,40xy.23xy和34xy为题设两条切线方程分别).3(2xyoxy·)0,3(··)3,23(34xy62xy342xxy所求面积为23032322)96(dxxxdxxA.49处的法线所围及其在点：计算由抛物线例)1,21(272xy成的平面图形的面积．解：,1yy.1)1,21(y处的在点)1,21(22xyoxy法线方程为.023yx的交点为和02322yxxy.)3,29()1,21(和)3,29(·)1,21(·xy22023yx所求面积为1332)6223(yyy132]2)23[(dyyyA.316所围成的平：求星形线例)0(sin,cos833ataytax面图形的面积．解：见右图oxyDa第一象限由对称性，所求面积是积为面积的四倍，即所求面2023sincos3sin4dtttataaydxA0420242)sin1(sin12dttta)221436522143(122a.832a所围成的面积．：求椭圆例192222byax解：见右图oxy第一由对称性，所求面积是求面积为象限面积的四倍，即所aydxA04椭圆的参数方程为tbytaxsincos20sinsin4dttatba202sin4tdtab20)2cos1(2dttab.ab所围成的面积．：试求双纽线例2cos1022ar解：见右图由对称性，所求面积是第一象限面积的四倍，402)(214dA即所求面积为4022cos2da4022sina.2a积．所围成的平面图形的面：求心形线例)cos1(11ar解：见右图由对称性，所求面积是drA02)(212da022)cos1(da02)22cos1cos21(02)2sin41sin223(a.232a的圆锥体的体积．，高为：求底园半径为例HR12解：建立坐标系如右图oxyyHRxHyHπR0322)3(所求体积为dyyHRπVH02)(.312HπR椭球轴旋转一周，得一旋转绕：将椭圆例xbyax1132222体，求其体积．解：建立坐标系如右图oxyadxxaabπ02222)(2aadxyπV2axxaaπb03222)3(2.342πab所求体积为绕：求摆线例)20()cos1()sin(14πtta,yttax的体积．轴旋转一周所得旋转体x解：建立坐标系如右图oxy所求体积为a220323)coscos3cos31(dttttπaadxyπV2022033)cos1(dttaπ2023]cos)sin1()2cos1(23cos31[dtttttπa.532aπ轴旋转所绕：求曲线例xbaabyx)0()(15222得旋转体的体积．oxyaa解：建立坐标系如右图所求体积为aaxab222)[(Vdxxab])(222adxxab0228aaxaxaxb0222]arcsin22[8.222ba轴旋转所得旋轴和分别绕：求例yxyx16)5(1622转体的体积．oxy44解：建立坐标系如右图4422)165[(xVx轴所得立体体积为绕xdxx])165(22dxx4021640402]4arcsin216162[40xxx.1602oxy19轴所得立体体积为绕y912])5(16[dyyVy913)5(3128y.3256反常积分）：计算下列广义积分（例17.1...