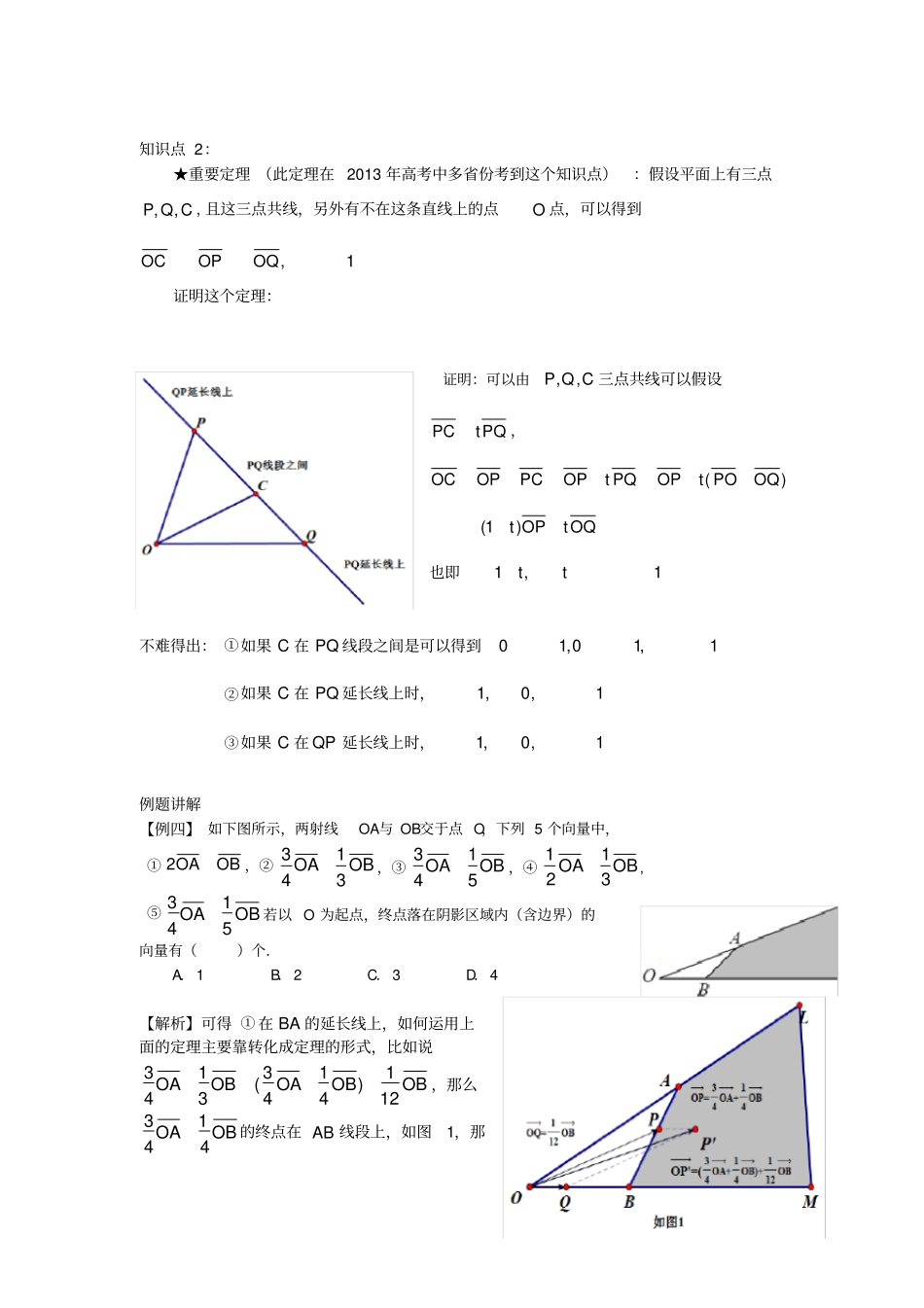
向量复习知识点1:两个不为零的向量a,b平行,①)0(ba②如果ba,可以用直角坐标系的坐标表示,那么设),(),,(qpbnma,那么npmq③如果ba,可以用两个不共线的基向量dc,表示,比如说dncma,dqcpb,那么基向量前面的系数成比例,也就是npmq在这里强调其实后面两点是一样的,因为向量的坐标表示法引进前身是用直角坐标系的两个垂直的单位向量ji,,比如),(nma,也即是jnima,为了方便,我们写成坐标形式,而③这点其实是②的一般形式,就是③讲两个基向量推广到了不垂直的情况。用这个知识点的例题比如说:【例一】设a与b是两个不共线的向量,且向量ab与(2)ba共线,则的值为.【解析】要求的两个向量就是用a与b作为基底的,那么这两个向量共线可以得到前面的系数成比例,也即是121,也即21【例二】在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F,若ACauuurr,BDbuuurr,则AFuuur=()A.1142abrrB.2133abrrC.1124abrrD.1233abrr【解析】比如说运用这个知识点首先本题的难点在于F点的位置,其在DC中的位置比例,所以首先要确定其位置在哪里,所以,我们设DCDF那么我们就可以用一个FEA,,共线来确定的值所以我们可以用AFAE,用相同基向量表示这两个向量,然后用系数比例的关系求出这个的值ABADADABADADACADAOAE414321)(4121412121ABADDCADDFADAF则3141143baBDACOCBOOBAOOCBOABADAF313231323432)(31)(31【例三】如图,在△ABC中,点M为BC的中点,A、B、C三点坐标分别为(2,﹣2)、(5,2)、(﹣3,0),点N在AC上,且NCAN2,AM与BN的交点为P,求:(1)点P分向量AM所成的比的值;(2)P点坐标.【解析】这题例题也是同样的道理,(1)主要求P点,假设AMAP,因为NPB,,三点共线,所以BNBP,用基向量BCBA,表示,再用待定系数法求得λ的值。ABBCABBCABBCABACBCAMBCMPBMBP)1(2))(1(2121))(1(2121)1(21ABBCBCABBCACBCCNBCBN3132)(3131所以54)1(2231)1(322,所以分向量AM所成的比的值为41(2)用比例的方法可以得到P)52,56((★★总结方法:在图中有未知线段的比例不知道,就可以先设其线段比例为,然后利用一个三点共线的两向量平行来求解的值。)知识点2:★重要定理(此定理在2013年高考中多省份考到这个知识点):假设平面上有三点CQP,,,且这三点共线,另外有不在这条直线上的点O点,可以得到1,OQOPOC证明这个定理:证明:可以由CQP,,三点共线可以假设PQtPC,)(OQPOtOPPQtOPPCOPOCOQtOPt)1(也即1,1tt不难得出:①如果C在PQ线段之间是可以得到1,10,10②如果C在PQ延长线上时,1,0,1③如果C在QP延长线上时,1,0,1例题讲解【例四】如下图所示,两射线OA与OB交于点O,下列5个向量中,①OBOA2,②OBOA3143,③OBOA5143,④OBOA3121,⑤OBOA5143若以O为起点,终点落在阴影区域内(含边界)的向量有()个.A.1B.2C.3D.4【解析】可得①在BA的延长线上,如何运用上面的定理主要靠转化成定理的形式,比如说OBOBOAOBOA121)4143(3143,那么OBOA4143的终点在AB线段上,如图1,那么OBOBOA121)4143(就会在如图的阴影部分内。同理可以将③OBOA3143转化为OBOBOAOBOA20141435143将④OBOA3121转化为OBOBOAOBOA6121213121将⑤OBOA5143转化为OBOBOAOBOA20941435143【例五】(2013安徽卷理9)在平面直角坐标系中,O是坐标原点,两定点A,B满2||||OBOAOBOA,则点集},,1||||,|{ROBOAOPP所表示的区域面积是(A)22(B)32(C)24(D)34【解析】2||||OBOAOBOA,可以得到2||||OBOA,且两个向量的夹角为60°,如图可以将两个向量放到半径为2的圆内,如图2。且由1||||,可得10,1||0,那么当10,10时,可知P点形成的区域为图中灰色区域当10,10,将问题转化为OBAOOBOAOP,那么P点形成的区域则是紫色的区域当10,10,将问题转化为BOAOOBOAOP那么P点形成的区域是红色的区域当10,10,将问题转化为BOOAOBOAOP那么P点形成的区域是黄色的区域所以,综上所述可得P点形成的区域为一个长为32,宽为2的矩形区域,即面积为34,所以答案选D。知识点3:向量的基本要素求解:一般求解向量的基本要素,主要分为求解向量之间的夹角和向量的模长。那么要求这几个要素必须要明白其可求解的途径:①求解模长1)如果向量a的坐标),...