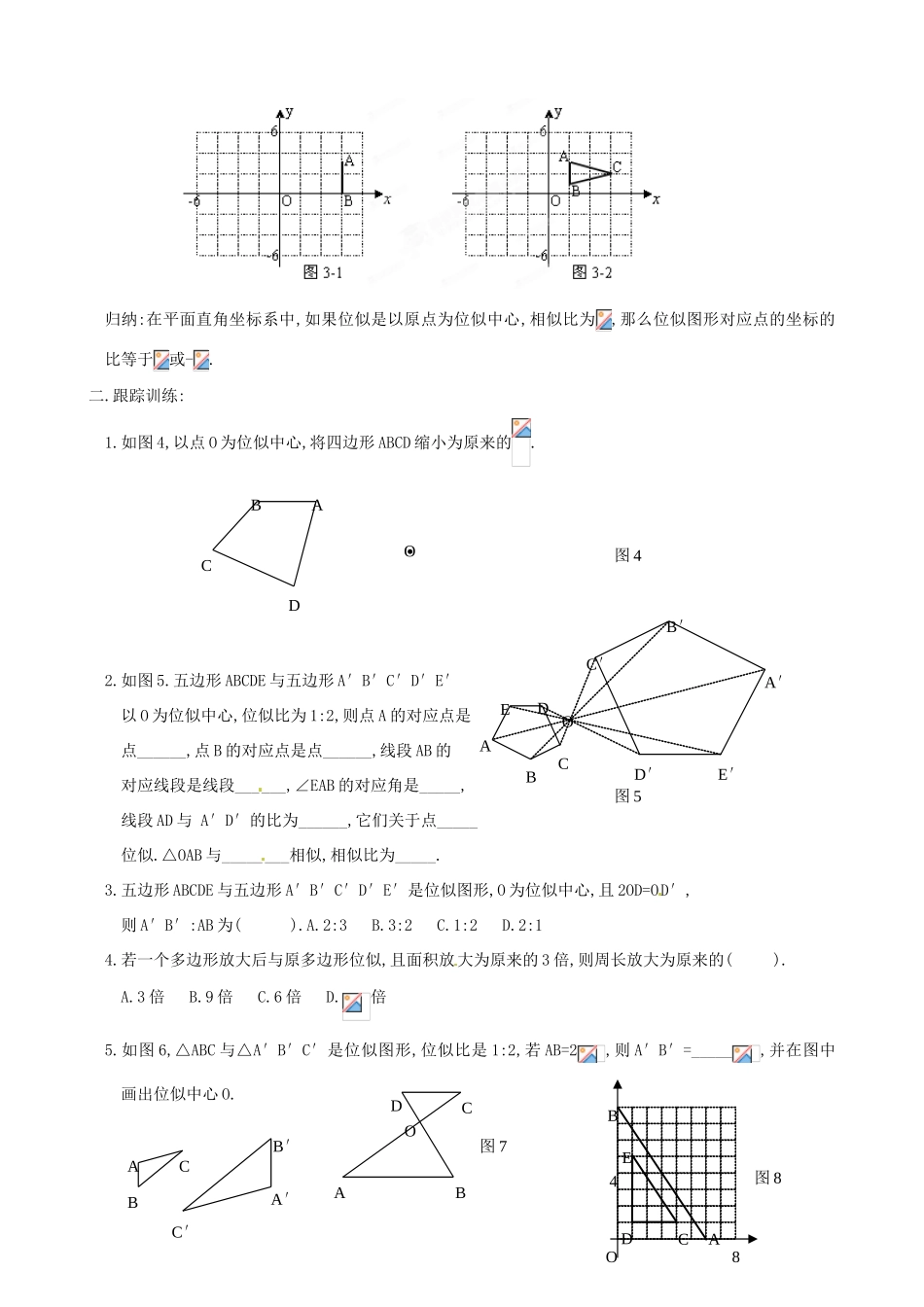
课题:27.3位似学习目标:1.能识别位似图形,并能找出位似中心.2.会利用位似将一个图形放大或缩小.3.能说出在平面直角坐标系中,关于原点位似的两个图形的坐标与位似比之间的关系.重点:利用位似将一个图形放大或缩小.难点:在平面直角坐标系中,如果位似是以原点为位似中心,根据位似比写出对应点的坐标.学法指导:同伴互助,小组合作.一.知识盘点:1.位似图形(如图1):两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,像这样的两个图形叫做位似图形,这个点叫做位似中心.2.利用位似将一个图形放大或缩小.例1:如图2,以点O为位似中心将△ABC放大为原来的2倍.3.例2:如图3-1所示,在平面直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为,把线段AB缩小,观察对应点之间坐标的变化,你有什么发现?例3:如图3-2所示,△ABC的三个顶点坐标分别为A(2,3)、B(2,1)、C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现?ABC图2O归纳:在平面直角坐标系中,如果位似是以原点为位似中心,相似比为,那么位似图形对应点的坐标的比等于或-.二.跟踪训练:1.如图4,以点O为位似中心,将四边形ABCD缩小为原来的.2.如图5.五边形ABCDE与五边形A′B′C′D′E′以O为位似中心,位似比为1:2,则点A的对应点是点______,点B的对应点是点______,线段AB的对应线段是线段______,∠EAB的对应角是_____,线段AD与A′D′的比为______,它们关于点_____位似.△OAB与________相似,相似比为_____.3.五边形ABCDE与五边形A′B′C′D′E′是位似图形,O为位似中心,且2OD=OD′,则A′B′:AB为().A.2:3B.3:2C.1:2D.2:14.若一个多边形放大后与原多边形位似,且面积放大为原来的3倍,则周长放大为原来的().A.3倍B.9倍C.6倍D.倍5.如图6,△ABC与△A′B′C′是位似图形,位似比是1:2,若AB=2,则A′B′=_____,并在图中画出位似中心O.DCBAO图4OCDEABD′E′A′B′C′图5CABA′C′B′ABOCD图7OCABED图8846.如图7,DC∥AB,OA=2AC,则△OCD△OAB的位似比是________.7.如图8,以某点为位似中心,将△AOB矩形位似变换得到△CDE,记△AOB与△CDE对应边的比为,在位似中心和的值分别为().A.(0,0)2B.(2,2)、C.(2,2)、2D.(2,2)、38.一个三角形的三个顶点的坐标分别是A(0,0)、B(2,2)、C(3,1),以A为位似中心,试将△ABC放大,使放大后的△AEF与△ABC的对应边的比2:1,则放大后的三角形各顶点的坐标分别为A__________、E_____________、F______________.2.三.变式训练:9.如图9,△ABC和△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是_________.10.如图10,某学习小组在讨论“变化的鱼”时,知道大鱼和小鱼是位似图形,则小鱼上的点对应大鱼上的点是().A.B.C.D.11.如图11所示,△ABC中,A、B两个顶点在轴的上方,点C的坐标是(-1,0),以点C为位似中心,在轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是,则点B的横坐标是().A.B.C.D.12.如图12,在6×8的网格中,每个小正方形的边长均为1,点O图910O4A′B′C′ABC图102-1CB′A′AOB图1111-1-1和△ABC的的顶点均在小正方形的顶点上.⑴.以O为位似中心,在网格中作△A′B′C′和△ABC位似,且位似比为1:2;⑵.连结⑴中的AA′,求四边形AA′C′C的周长(结果保留根号).13.如图13,每个小正方形的边长都为1,点B的坐标为(-1,-1).⑴.把△ABC向左平移8格后,得到△A1B1C1,画出△A1B1C1并写出点B1的坐标;⑵.把△ABC绕点C顺时针旋转90°后得到△A2B2C,画出△A2B2C并写出点B2的坐标;⑶.把△ABC以点A为位似中心,使放大前后位似比为1:2,画出放大后的△AB3C3.14.如图14,已知点O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1).⑴.以O点为位似中心,在轴的左侧,将△OBC放大到原来的2倍,画出△OB′C′;⑵.分别写出B、C两点的对应点B′、C′的坐标;ABCO图12⑶.如果△OBC内部一点M的坐标为,写出M的对应点M′的坐标.图14-52OCB图6-2图6O