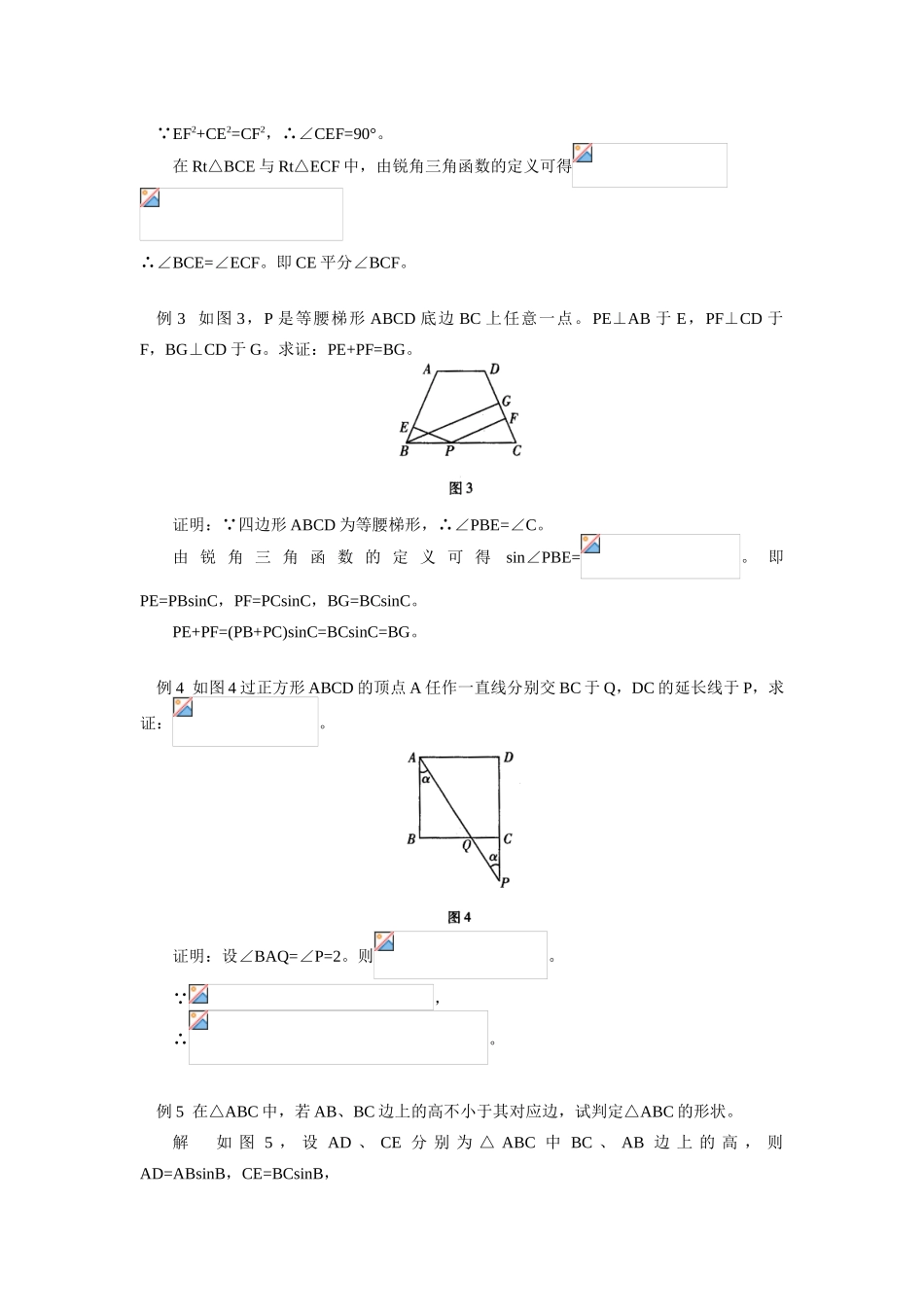
应用锐角三角函数的定义证几何题陈东秉锐角三角函数的定义,可以把一个直角三角形中边与角的关系联系起来,从而使许多几何问题有了纯粹几何证法所容纳不了的天地。请看下面几例。例1如图1,M为正方形ABCD中AB边的中点,E是AB延长线上一点,MN⊥DM且交∠CBE的平分线于N,求证:MD=MN。证明:设AM=BM=1,BF=x,则AD=2,MF=x+1,NF=BF=x。∵MN⊥DM,∠A=∠ABC,∴∠ADM=∠FMN。在Rt△ADM和Rt△FMN中,由锐角三角函数的定义可得,,。∴。解得x=1。即NF=1,MF=2。∴Rt△ADM≌Rt△FMN。∴DM=MN。例2如图2,E是正方形ABCD中边AB的中点,F在AD边上,且DF=3AF,求证:CE平分∠BCF。证明:连EF,设正方形ABCD的边长为4。则AE=BE=2,AF=1,DF=3。EF2=12+22=5。CE2=22+42=20,CF2=32+42=25。∵EF2+CE2=CF2,∴∠CEF=90°。在Rt△BCE与Rt△ECF中,由锐角三角函数的定义可得∴∠BCE=∠ECF。即CE平分∠BCF。例3如图3,P是等腰梯形ABCD底边BC上任意一点。PE⊥AB于E,PF⊥CD于F,BG⊥CD于G。求证:PE+PF=BG。证明:∵四边形ABCD为等腰梯形,∴∠PBE=∠C。由锐角三角函数的定义可得sin∠PBE=。即PE=PBsinC,PF=PCsinC,BG=BCsinC。PE+PF=(PB+PC)sinC=BCsinC=BG。例4如图4过正方形ABCD的顶点A任作一直线分别交BC于Q,DC的延长线于P,求证:。证明:设∠BAQ=∠P=2。则。∵,∴。例5在△ABC中,若AB、BC边上的高不小于其对应边,试判定△ABC的形状。解如图5,设AD、CE分别为△ABC中BC、AB边上的高,则AD=ABsinB,CE=BCsinB,AD+CE=(AB+BC)sinB。∵AD≥BC,CE≥AB,∴AD+CE≥AB+BC,即(AB+BC)sinB≥AB+BC,则可得sinB≥1。∵sinB≤1,∴sinB=1,∠B=90°,因此,△AB=BC,因此D、E两点与B重合,由题设知AB≥BC,BC≥AB,则AB=BC,因此,△ABC为等腰直角三角形。从以上数例可以看出,用此法证某些几何题可不添或少添辅助线,以计算代替逻辑推理从而减少证题中的困难。