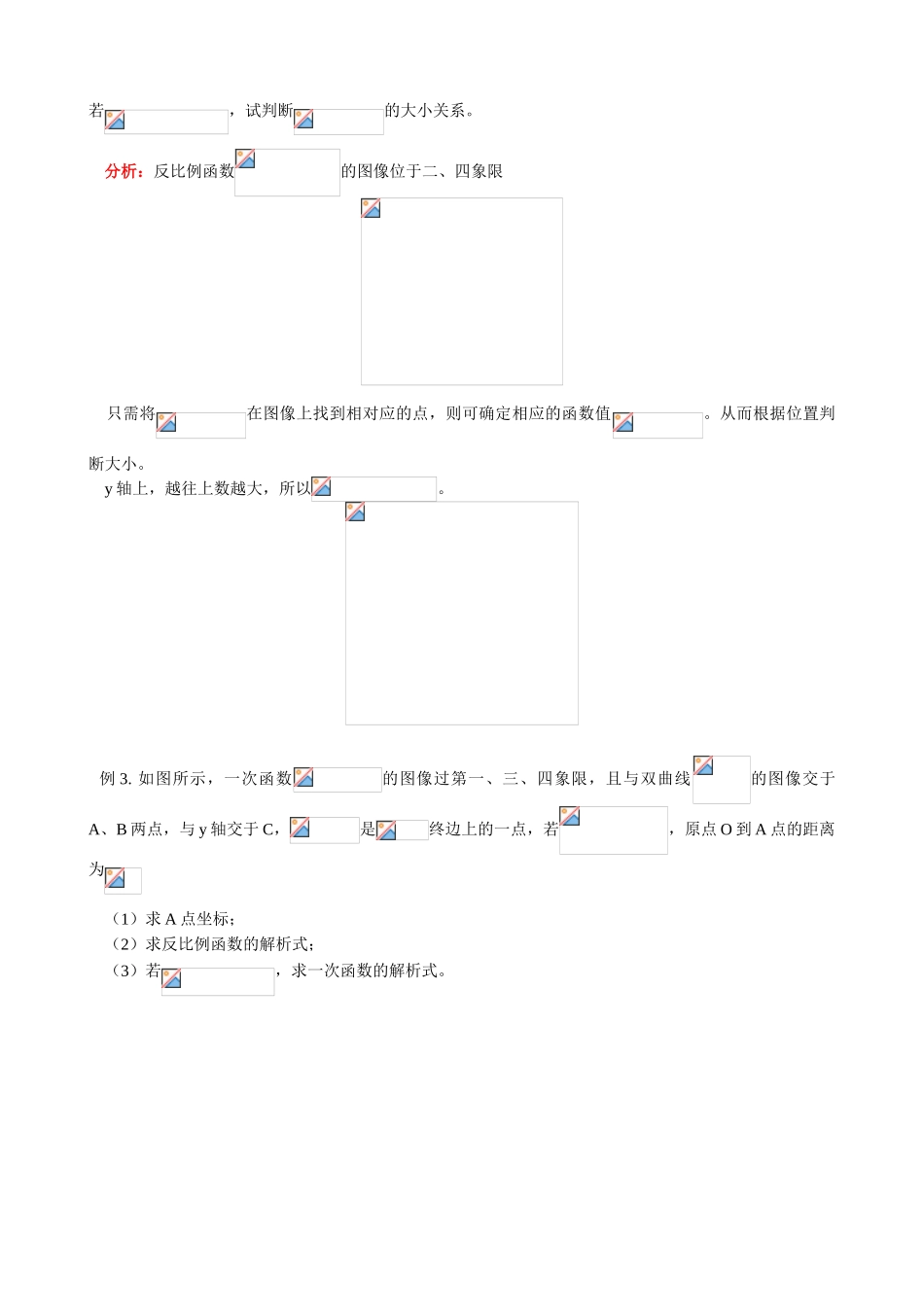
八年级数学暑假专题辅导——函数解题中的数学思想应用重点、难点数学思想的应用【典型例题】一.方程思想的应用例1.已知点P(x,x+y)与点Q(y+5,x-7)关于x轴对称,则点Q坐标为______。分析:P点关于x轴对称时,横坐标不变,纵坐标相反构造方程组解得:∴Q点坐标为(4,-3)例2.已知一次函数的图像经过第一、二、三象限,求m的值。分析:一次函数条件:x的次数为1即:得:解得:而当此时图像经过一、三、四象限不符合题意,舍去故m=3例3.已知:在△ABC中,,P为AB上一动点(P不与A、B重合),过点P作PE//BC交AC于E,连结BE,设AP=x,△BPE的面积为y,求y与x之间的函数关系,并求自变量x的取值范围。分析:∴知道PE的长、EC的长是关键,而PE、EC与三角形相似有关。所以此题借助比例式找出PE、EC与x之间的等量关系。即:用含x的式子表示PE、EC,进而得到函数关系式。解:二.数形结合思想的应用例1.一次函数的图像经过第_______象限。分析:充当中的k,此时大于0充当中的b,此时小于0则依据直线,当的图象示意图:可知图像经过一、三、四象限。例2.已知反比例函数是反比例函数图象上的三个点,若,试判断的大小关系。分析:反比例函数的图像位于二、四象限只需将在图像上找到相对应的点,则可确定相应的函数值。从而根据位置判断大小。y轴上,越往上数越大,所以。例3.如图所示,一次函数的图像过第一、三、四象限,且与双曲线的图像交于A、B两点,与y轴交于C,是终边上的一点,若,原点O到A点的距离为(1)求A点坐标;(2)求反比例函数的解析式;(3)若,求一次函数的解析式。分析:此题关键是在平面直角坐标系中借助及,在Rt△中求A点坐标。从而进一步借助到y轴距离等于,求出b,确定一次函数的解析式。解:(1)设点A坐标为(a,b),且过A作轴交x轴于M则在所以点A坐标为(5,1)(2)此反比例函数解析式为(3),且(OC=|b|,C在x轴下方)∴一次函数解析式为:又 直线过点∴一次函数解析式为三.分类讨论思想的应用例1.已知点N在x轴下方,且到x轴距离为2,到y轴距离为,则点N的坐标为_________。分析:设点N坐标为(x,y)由题意得:则又 点N在x轴下方,y<0例2.已知直线与直角坐标系的两坐标轴围成的三角形的面积为9,则直线解析式为__________。分析:设直线与x轴交点为A,与y轴交点为B则∴直线解析式为例3.已知点A为平面直角坐标系内第四象限夹角平分线上一点,且OA=5,试在坐标轴上找一点C,使得△AOC为等腰三角形,并写出C点坐标。分析:首先应分别在x轴和y轴上找点C其次,△AOC应分类找:(1)OA为腰;(2)OA为底当C点在x轴上时当C点在y轴上时四.转化思想的应用例1.已知一次函数的图像经过二、三、四象限,求k的取值范围。分析:直线经过二、三、四象限则得:所以例2.待定系数解题(转化为方程组)如:已知与成正比例,其中m,n是常数,当时,;当时,,求y与x的函数关系。分析:设当时,得:当时,得:解方程组解得:所求函数关系式为:例3.如图所示,直线与y轴交于点A(0,3)与x轴交于点B,正方形OPQR的两边在坐标轴上,Q在直线AB上,OP:PB=1:2,求直线的解析式。分析:求直线AB解析式,需要知道A、B坐标。而A点(0,3),则OA=3,求B点即可,即求OB长,此问题转化为几何问题。又知PQRO为正方形,设正方形边长为x,则∴B点坐标为(6,0)∴直线解析式为五.几何解题思想的综合应用例:已知反比例函数和一次函数,其中一次函数的图象经过(a,b),(a+1,b+k)两点。(1)求反比例函数的解析式;(2)如图所示,已知点A是上述两个函数的图象在第一象限的交点,求点A的坐标;(3)利用(2)的结果,回答:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由。分析:(1)由一次函数的图象经过两点(a,b),(a+1,b+k),代入消去a,b,可得k=2,进而可确定反比例函数的关系式。(2)将联立成方程组,易求出点A的坐标;(3)应根据OA为腰和底进行分类,结合(2)探求出点P的存在性。解:(1)依题意可得:两式相减,得所以反比例函数的解析式为(2)由,得,经检验都是原方程组的解。因为A点在第一象限,所以A点...