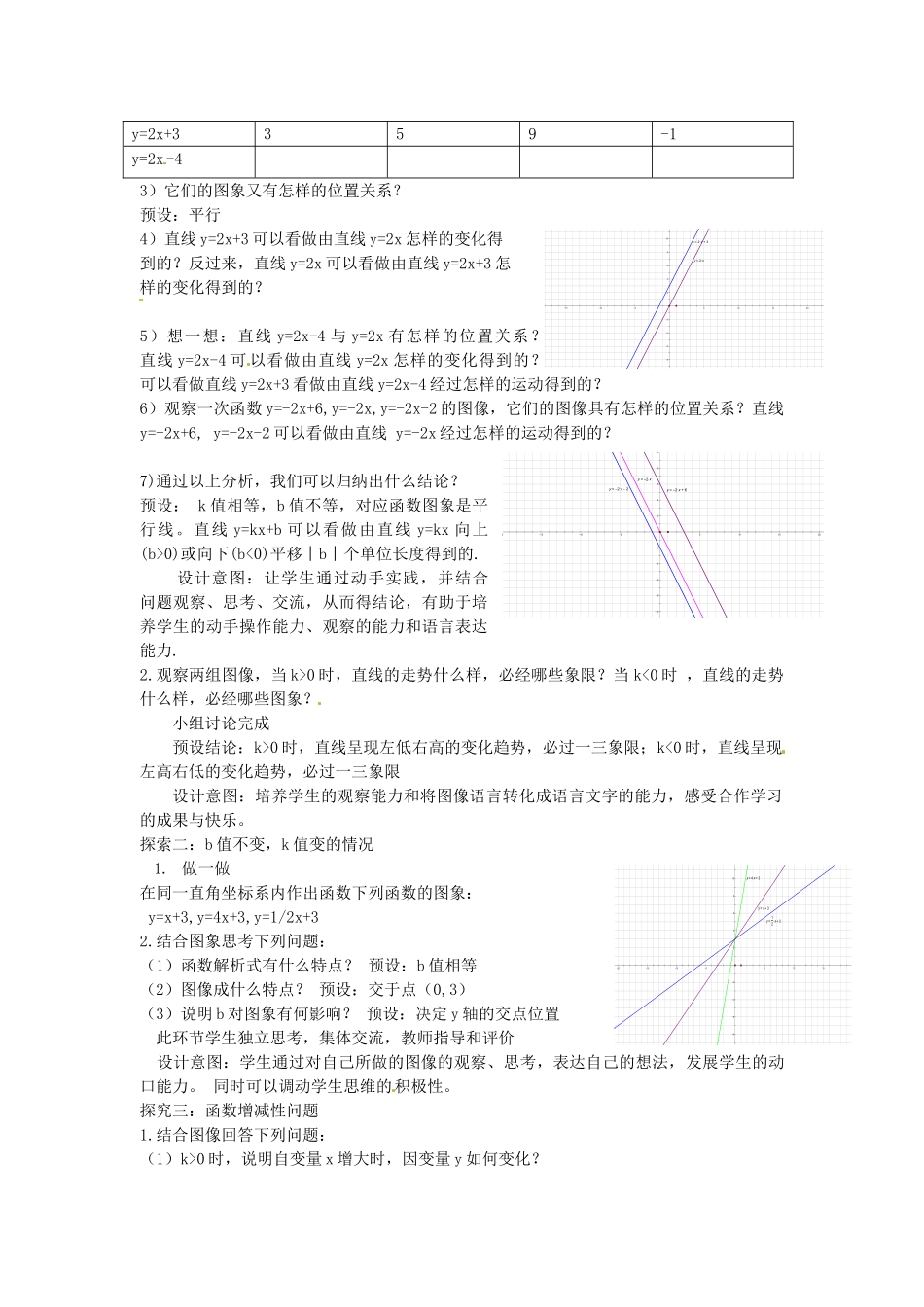
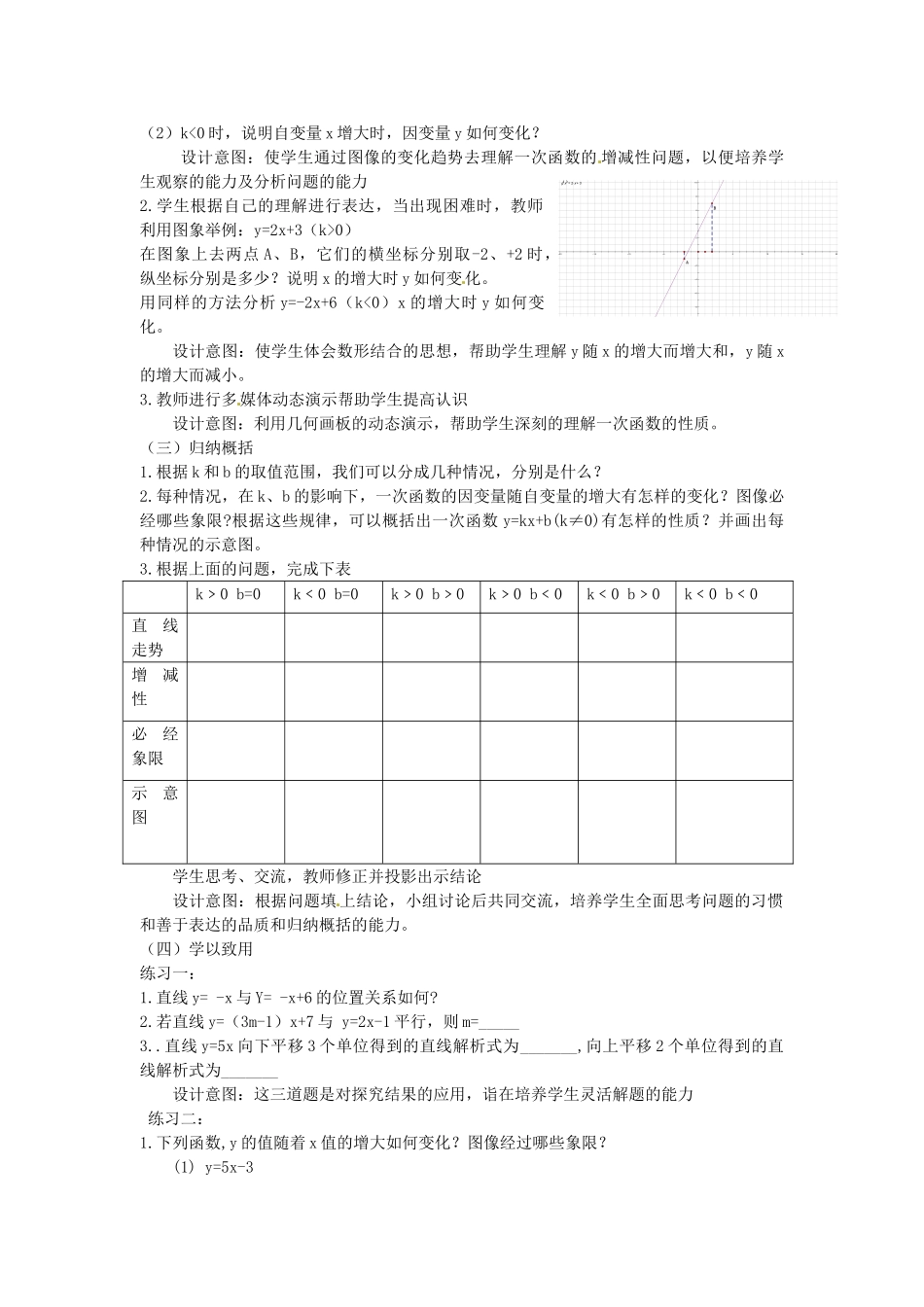
一次函数的性质一、教学目标三、教学方法与手段预设y=2x,y=2x+3,y=--x+3,y=10x-1等以y=2x,y=2x+3为例提出问题:2..像y=2x这样的函数又称为什么函数?预设:正比例函数3.正比例函数与一次函数又怎样的关系?预设:正比例函数是特殊的一次函数4你能在同一坐标系内作出函数y=2x,y=2x+3的图象吗?此环节处理方式:学生独立思考,集体交流,教师指导和评价设计意图:通过通过复习旧知识,检查学生对已学知识的掌握情况和作图能力,为下个环节结合图象探索一次函数的性质作准备.(二)探索新知探索一:k值不变,b值变的情况1.结合图象思考下列问题(小组讨论交流):1)函数y=2x,y=2x+3中的x的系数有什么关系?预设:相同2)当x取相同值时,它们相应的函数值有什么关系?举例:x013-2y=2x026-4y=2x+3359-1y=2x-43)它们的图象又有怎样的位置关系?预设:平行4)直线y=2x+3可以看做由直线y=2x怎样的变化得到的?反过来,直线y=2x可以看做由直线y=2x+3怎样的变化得到的?5)想一想:直线y=2x-4与y=2x有怎样的位置关系?直线y=2x-4可以看做由直线y=2x怎样的变化得到的?可以看做直线y=2x+3看做由直线y=2x-4经过怎样的运动得到的?6)观察一次函数y=-2x+6,y=-2x,y=-2x-2的图像,它们的图像具有怎样的位置关系?直线y=-2x+6,y=-2x-2可以看做由直线y=-2x经过怎样的运动得到的?7)通过以上分析,我们可以归纳出什么结论?预设:k值相等,b值不等,对应函数图象是平行线。直线y=kx+b可以看做由直线y=kx向上(b>0)或向下(b<0)平移︱b︱个单位长度得到的.设计意图:让学生通过动手实践,并结合问题观察、思考、交流,从而得结论,有助于培养学生的动手操作能力、观察的能力和语言表达能力.2.观察两组图像,当k>0时,直线的走势什么样,必经哪些象限?当k<0时,直线的走势什么样,必经哪些图象?小组讨论完成预设结论:k>0时,直线呈现左低右高的变化趋势,必过一三象限;k<0时,直线呈现左高右低的变化趋势,必过一三象限设计意图:培养学生的观察能力和将图像语言转化成语言文字的能力,感受合作学习的成果与快乐。探索二:b值不变,k值变的情况1.做一做在同一直角坐标系内作出函数下列函数的图象:y=x+3,y=4x+3,y=1/2x+32.结合图象思考下列问题:(1)函数解析式有什么特点?预设:b值相等(2)图像成什么特点?预设:交于点(0,3)(3)说明b对图象有何影响?预设:决定y轴的交点位置此环节学生独立思考,集体交流,教师指导和评价设计意图:学生通过对自己所做的图像的观察、思考,表达自己的想法,发展学生的动口能力。同时可以调动学生思维的积极性。探究三:函数增减性问题1.结合图像回答下列问题:(1)k>0时,说明自变量x增大时,因变量y如何变化?1086422468201510551015y=12∙x+3y=4∙x+3y=x+31086422468151055101520y=2∙x+3y=2∙x10864224681020151055101520y=2∙x2y=2∙xy=2∙x+6(2)k<0时,说明自变量x增大时,因变量y如何变化?设计意图:使学生通过图像的变化趋势去理解一次函数的增减性问题,以便培养学生观察的能力及分析问题的能力2.学生根据自己的理解进行表达,当出现困难时,教师利用图象举例:y=2x+3(k>0)在图象上去两点A、B,它们的横坐标分别取-2、+2时,纵坐标分别是多少?说明x的增大时y如何变化。用同样的方法分析y=-2x+6(k<0)x的增大时y如何变化。设计意图:使学生体会数形结合的思想,帮助学生理解y随x的增大而增大和,y随x的增大而减小。3.教师进行多媒体动态演示帮助学生提高认识设计意图:利用几何画板的动态演示,帮助学生深刻的理解一次函数的性质。(三)归纳概括1.根据k和b的取值范围,我们可以分成几种情况,分别是什么?2.每种情况,在k、b的影响下,一次函数的因变量随自变量的增大有怎样的变化?图像必经哪些象限?根据这些规律,可以概括出一次函数y=kx+b(k≠0)有怎样的性质?并画出每种情况的示意图。3.根据上面的问题,完成下表k﹥0b=0k﹤0b=0k﹥0b﹥0k﹥0b﹤0k﹤0b﹥0k﹤0b﹤0直线走势增减性必经象限示意图学生思考、交流,教师修正并投影出示结论设计意图:根据问题填上结论,小组讨论后共同交流,培养学生全面思考问题的习惯和善于表达的品...