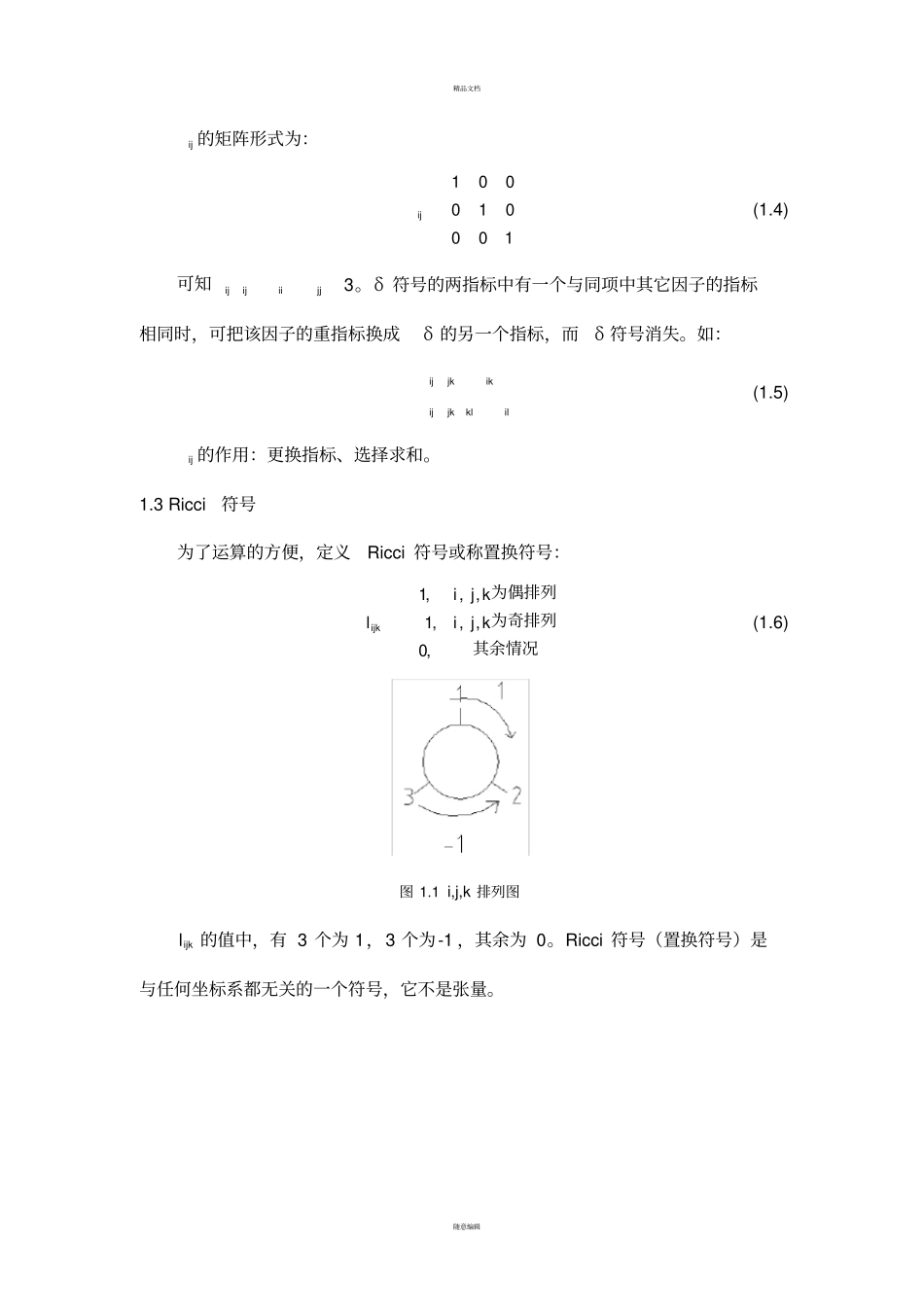
精品文档随意编辑一、知识总结1张量概念1.1指标记法哑标和自由指标的定义及性质自由指标:在每一项中只出现一次,一个公式中必须相同。性质:在表达式或方程中自由指标可以出现多次,但不得在同项内重复出现两次。哑标:一个单项式内,在上标(向量指标)和下标(余向量指标)中各出现且仅出现一次的指标。性质:哑标可以把多项式缩写成一项;自由指标可以把多个方程缩写成一个方程。例:333323213123232221211313212111BxAxAxABxAxAxABxAxAxA(1.1)式(1.1)可简单的表示为下式:ijijBxA(1.2)其中:i为自由指标,j为哑标。特别区分,自由指标在同一项中最多出现一次,表示许多方程写成一个方程;而哑标j则在同项中可出现两次,表示遍历求和。在表达式或者方程中自由指标可以出现多次,但不得在同项中出现两次。1.2Kronecker符号定义ij为:jijiij,0,1(1.3)精品文档随意编辑ij的矩阵形式为:100010001ij(1.4)可知3ijijiijj。δ符号的两指标中有一个与同项中其它因子的指标相同时,可把该因子的重指标换成δ的另一个指标,而δ符号消失。如:ijjkikijjkklil(1.5)ij的作用:更换指标、选择求和。1.3Ricci符号为了运算的方便,定义Ricci符号或称置换符号:其余情况为奇排列为偶排列,0,,,1,,,1kjikjilijk(1.6)图1.1i,j,k排列图ijkl的值中,有3个为1,3个为-1,其余为0。Ricci符号(置换符号)是与任何坐标系都无关的一个符号,它不是张量。精品文档随意编辑1.4坐标转换图1.2坐标转换如上图所示,设旧坐标系的基矢为ie,新坐标系的基矢为'ie。有''ijijijeeee'ie在ie下进行分解:''11'22'33'iiiiijjeeeeeje在'ie下进行分解:''''1'12'23'3'jjjjijieeeee其中,''''cos(,)ijijijjieeeeee为新旧坐标轴间的夹角余弦,称为坐标转换系数。空间点P在新老坐标系矢径:0rrrexrexrjjii(1.7)其中'0r为上图中坐标原点的位移矢量。将'r向新坐标轴上投影的矢量的分量:'''''''''''''''''0000()()()()ikkikkiiikkijjikkijijijijrexeexxrrexeexeexxxx即由此得新坐标用老坐标表示的公式:ijjiixxx0)((1.8)类似地,将i向老坐标上投影,可以推导出老坐标用新坐标表示的公式:''0()jjiijxxx(1.9)特别的,当新旧坐标原点重合时,也即坐标轴仅发生旋转,此时'0()0ix,上两式的矩阵形式为:精品文档随意编辑'1''Txxxxx(1.10)由上可知,TI,是正交矩阵,则'1ij。综合以上可知:''''''''''''''''ijlklkiljkiljkikjkikjkijijijeeeeee(1.11)同理,可推出:''ijkikj将老坐标到新坐标的坐标转换称为正转换,''()iijxxx;将新坐标到老坐标的坐标转换称为正转换,'()jjixxx''iijjxdxdxx,其中'ijxx为常数,称'ijxJx为雅克比行列式。若J处处不为0,则说明存在相应的逆变化,即:'''jiijjixxxx1.5张量的分量坐标转换规律1.5.1一阶张量一阶张量在新老坐标系中的分解为:jjiieaeaa(1.12)其中:ijijee(1.13)则:ijijiieaeaa(1.14)得到:jijiaa(1.15)同理:jjiiee(1.16)精品文档随意编辑得:ijijaa(1.17)矢量是与一阶基矢相关联的不变量,可表示为一阶基矢的线性组合,此组合与坐标系的选择无关,故为一阶张量,标量为零阶张量。1.5.2二阶张量定义jiee为二阶基矢,写在一起,不作任何运算。由下式:ijijjjiieeee(1.18)可得坐标变换时二阶基矢的转换规律为:jinjminmnmnjmijieeeeeeee(1.19)又:jjiijjiiebeaebeaab(1.20)记:jiijbaB,jiijbaB(1.21)则:jiijjiijeeBeeBab(1.22)该式表示a与b并乘为一个坐标不变量,称为二阶张量。记为:jiijjiijeeBeeBB(1.23)将式(1.13)代入上式可得:ijnjmimnmnnjmiijBBBB(1.24)此分量转换可进一步推广到高阶张量。张量与坐标轴选择无关,故可独立于坐标系来表述。精品文档随意编辑2张量的代数运算2.1张量的加减假如A、B为同阶张量,将它们在同一坐标系下的同类型分量一一相加(减),得到的结果即为它们的和(差),记为)(BABA,例如:ijijBABA(2.1)显然,同阶张量进行加减运算后仍为同阶张量。2.2标量与张量的积张量A,标量λ,若AB,则:ijijAB(2.2)2.3张量的并积两个同维不同阶(同阶)张量A、B的并积C是一个阶数为A、B阶数之和的高阶张量。kjiijkeeeAA(2.3)mllmeeBB(2.4)mlkjiijklmeeeeeCBAC(2.5...