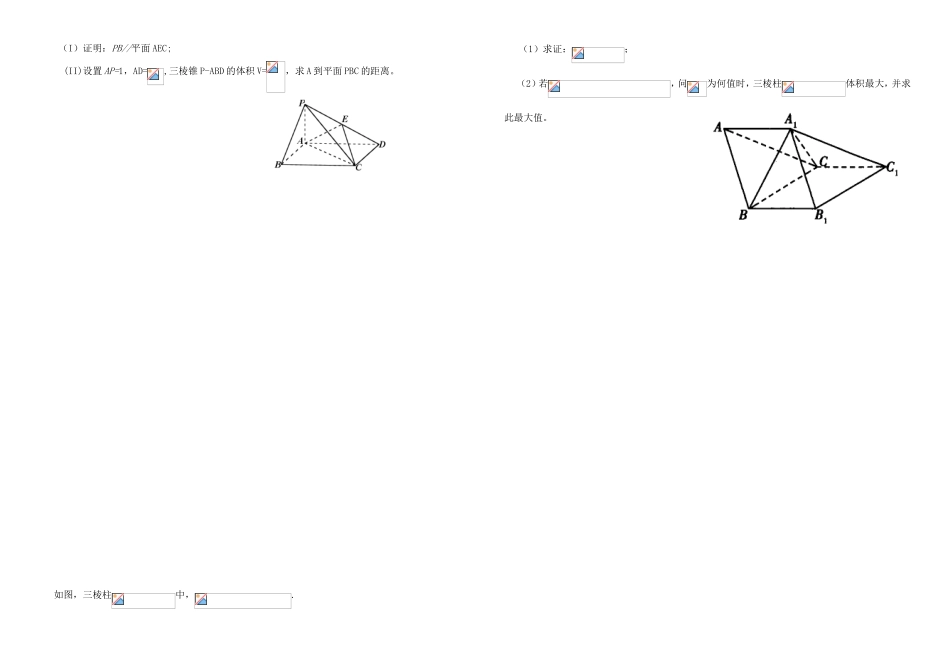
衡水万卷作业卷十八文数立体几何作业专练姓名:__________班级:__________考号:__________题号一二三总分得分一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)正方体的内切球与其外接球的体积之比为()A1∶B1∶3C1∶3D1∶9若正方体的棱长为,则以该正方体各个面的中心为顶点的凸多面体的体积为()A.B.3C.D.在二面角的两个面内,分别有直线,它们与棱都不垂直,则()A.当该二面角是直二面角时,可能,也可能B.当该二面角是直二面角时,可能,但不可能C.当该二面角不是直二面角时,可能,但不可能D.当该二面角不是直二面角时,不可能,也不可能如图,体积为的大球内有4个小球,每个小球的球面过大球球心且与大球球面有且只有一个交点,4个小球的球心是以大球球心为中心的正方形的4个顶点.为小球相交部分(图中阴影部分)的体积,为大球内.小球外的图中黑色部分的体积,则下列关系中正确的是()A.B.C.D.已知球的直径,A,B是该球面上的两点,,,则棱锥的体积为()A.B.C.D.设三棱柱的侧棱垂直于底面,所成棱的长都为a,顶点都在一个球面上,则该球的表面积为()A.B.C.D.若三棱锥的三条侧棱锥两两垂直,且侧棱长都相等,其外接球的表面积是,则其侧棱长为()A.B.C.D.已知正四棱锥中,,那么当该棱锥的体积最大时,它的高为()A.B.C.D.将边长为a的正方形ABCD沿对角线AC折叠,使,则三棱锥的体积为()A.B.C.D.正四面体的内切球球心到一个面的距离等于这个正四面体高的()A.B.C.D.设球的体积为,它的内接正方体的体积为,下列说法最合适的是()A.比大约多一半B.比大约多两倍半C.比大约多一倍D.比大约多一倍多已知平面截球面的圆。过圆心且与成二面角的平面截该球面得圆.若该球的半径为4,圆的面积为,则圆的面积为().A.B.C.D.二、填空题(本大题共4小题,每小题4分,共16分)已知三棱锥,,平面,其中,四点均在球的表面上,则球的表面积为.要做一个圆锥形漏斗,其母线长为,若要使圆锥形漏斗的体积最大,则其高应为。已知一个实心铁质的几何体的正视图.侧视图和俯视图都是半径为3的圆,将8个这样的几何体熔成一个实心的球,则该球的表面积为。已知平面平面平面则三棱锥外接球的表面积为。三、解答题(本大题共2小题,共24分)如图,四凌锥P—ABCD中,底面ABCD为矩形,PA⊥面ABCD,E为PD的中点。(I)证明:PB//平面AEC;(II)设置AP=1,AD=,三棱锥P-ABD的体积V=,求A到平面PBC的距离。如图,三棱柱中,.(1)求证:;(2)若,问为何值时,三棱柱体积最大,并求此最大值。衡水万卷作业卷十八文数答案解析一、选择题CCBDC【解析】由题可知一定在直径垂直的小圆面上,作过的小圆交直径于D,如图所示,设,则,此时所求的棱锥即分割成两个棱锥和,在和中,由已知条件可得,又因为SC为直径,所以所以,所以在中,所以x=4-x,解得,所以,所以为正三角形,所以.B【解析】三棱锥如(答图),由题意可知:球心在三棱柱上.下底面的中心.的连线的中点处,连接..,其中即为球的半径,由题意知:,所以半经所以球的表面积是.B【解析】依题意可以构造一个正方体,其体对角线就是外接球的直径.设侧棱长为,球半径为,,.C【解析】设正四棱锥的底面边长为,则高,所以体积.因为为定值,由均值不等式可得,即,当且仅当,即时,,此时高D【解析】设正方形的对角线.相较于点沿折起后依题意得,当时,,所以平面,于是三棱锥的高为,所以三棱锥的体积.C【解析】本题考查三棱锥的体积公式的应用.割补法解题的思想.球心到四面体各个面的距离都相等,都等于内切球的半径,连接求心与正四面体的四个顶点.把正四面体分成四个三棱锥,这四个三棱锥相等,高都为所以(其中为正四面体,一个面的面积,为正四面体的高)D【解析】设正方体的棱长为,则正方体的体积为,则球半径为,球体积,则选D.D【解析】设圆的半径为,球心为,平面,其中线段是圆的一条直径,连接OM,ON,MN,NA,NB过点M在平面内作的垂线交圆M于点C.由题意知是圆的一条弦,则有又为的中点,于是有又因此平面,又平面因此平面平面与重合,即点O,C,M,N四点共面,在四边形中,,.因此,球心到截面的距离,截面圆的半...