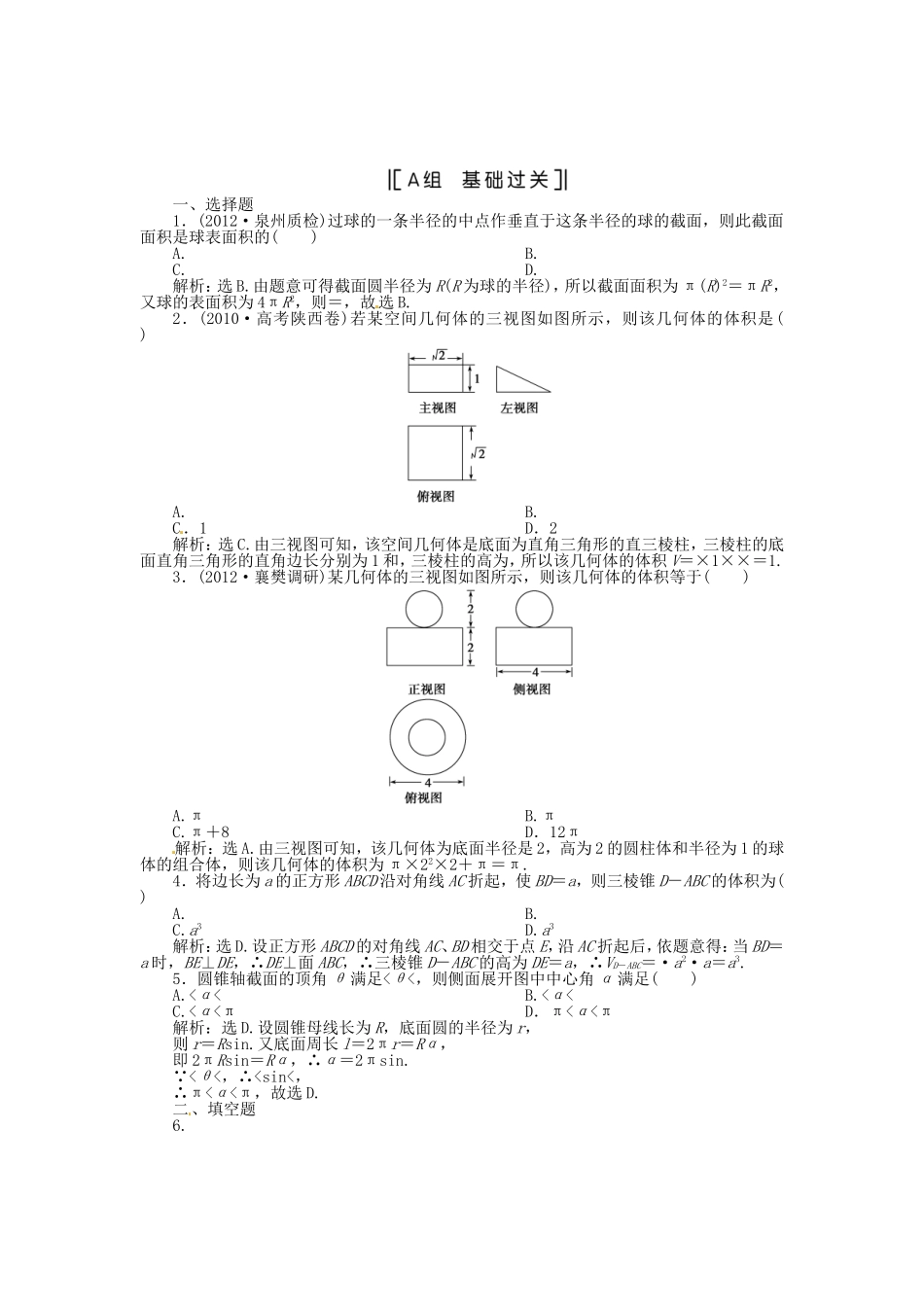
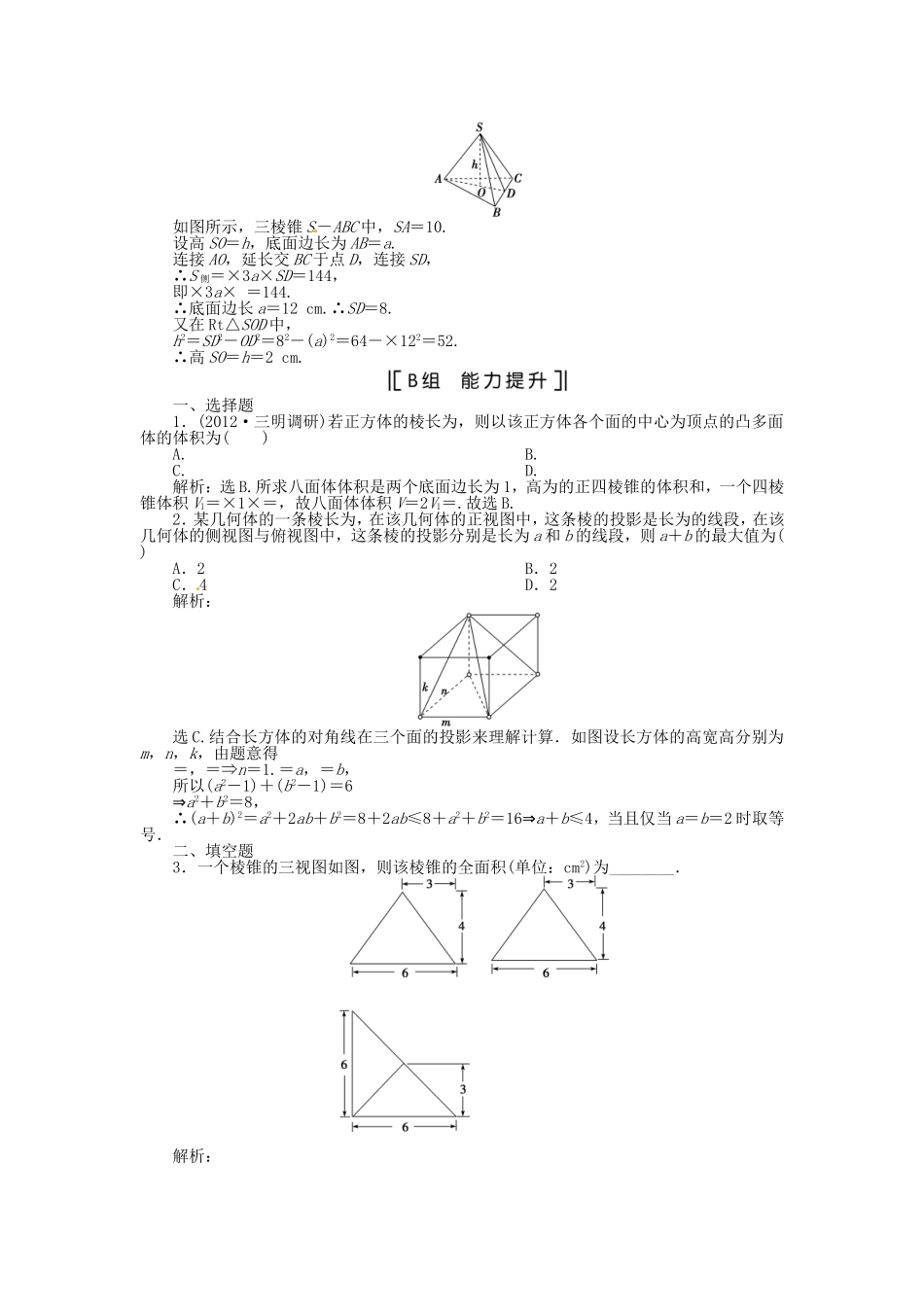
一、选择题1.(2012·泉州质检)过球的一条半径的中点作垂直于这条半径的球的截面,则此截面面积是球表面积的()A.B.C.D.解析:选B.由题意可得截面圆半径为R(R为球的半径),所以截面面积为π(R)2=πR2,又球的表面积为4πR2,则=,故选B.2.(2010·高考陕西卷)若某空间几何体的三视图如图所示,则该几何体的体积是()A.B.C.1D.2解析:选C.由三视图可知,该空间几何体是底面为直角三角形的直三棱柱,三棱柱的底面直角三角形的直角边长分别为1和,三棱柱的高为,所以该几何体的体积V=×1××=1.3.(2012·襄樊调研)某几何体的三视图如图所示,则该几何体的体积等于()A.πB.πC.π+8D.12π解析:选A.由三视图可知,该几何体为底面半径是2,高为2的圆柱体和半径为1的球体的组合体,则该几何体的体积为π×22×2+π=π.4.将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D-ABC的体积为()A.B.C.a3D.a3解析:选D.设正方形ABCD的对角线AC、BD相交于点E,沿AC折起后,依题意得:当BD=a时,BE⊥DE,∴DE⊥面ABC,∴三棱锥D-ABC的高为DE=a,∴VD-ABC=·a2·a=a3.5.圆锥轴截面的顶角θ满足<θ<,则侧面展开图中中心角α满足()A.<α