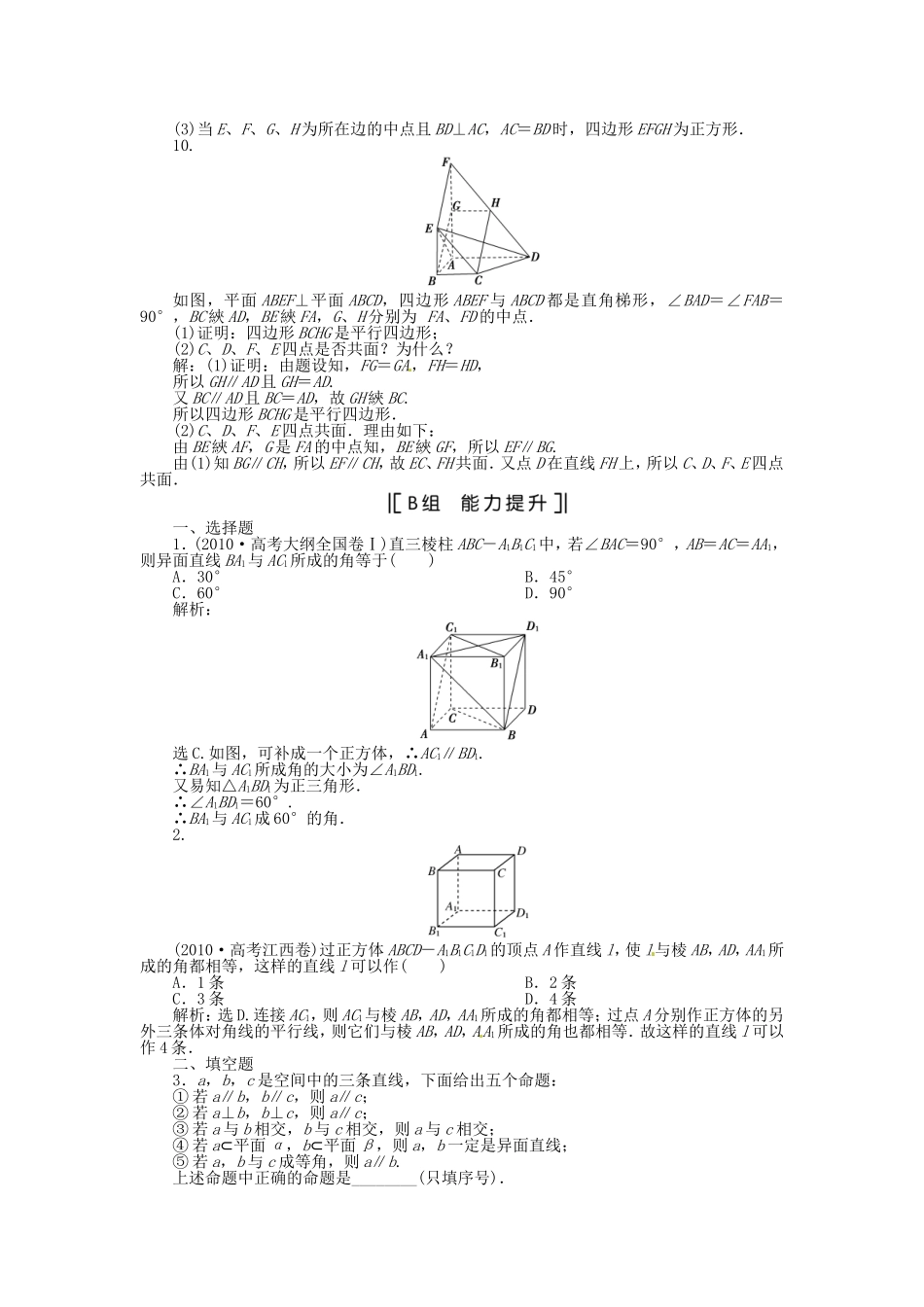
一、选择题1.以下几个命题中,正确命题的个数是()①不共面的四点中,其中任意三点不共线;②若点A、B、C、D共面,点A、B、C、E共面,则A、B、C、D、E共面;③若直线a、b共面,直线a、c共面,则直线b、c共面;④依次首尾相接的四条线段必共面.A.0B.1C.2D.3解析:选B.①正确;②从条件看出两平面有三个公共点A、B、C,但是若A、B、C共线,则结论不正确;③不正确,共面不具有传递性;④不正确,因为此时所得四边形的四条边可以不在一个平面上.2.(2012·南平调研)若异面直线a,b分别在平面α,β内,且α∩β=l,则直线l()A.与直线a,b都相交B.至少与a,b中的一条相交C.至多与a,b中的一条相交D.与a,b中的一条相交,另一条平行解析:选B.若a∥l,b∥l,则a∥b,故a,b中至少有一条与l相交,故选B.3.在正方体ABCD-A1B1C1D1中,过顶点A1与正方体其他顶点的连线与直线BC1成60°角的条数为()A.1B.2C.3D.4解析:选B.有2条:A1B和A1C1,故选B.4.如图是正方体或四面体,P、Q、R、S分别是所在棱的中点,这四个点不共面的一个图是()解析:选D.在A图中分别连接PS、QR,易证PS∥QR,∴P、S、R、Q共面;在C图中分别连接PQ、RS,易证PQ∥RS,∴P、Q、R、S共面.如图,在B图中过P、Q、R、S可作一正六边形,故四点共面,D图中PS与RQ为异面直线,∴四点不共面,故选D.5.正方体ABCD-A1B1C1D1,E,F分别是AA1,CC1的中点,P是CC1上的动点(包括端点),过点E、D、P作正方体的截面,若截面为四边形,则P的轨迹是()A.线段C1FB.线段CFC.线段CF和一点C1D.线段C1F和一点C解析:选C.如图,DE∥平面BB1C1C,∴平面DEP与平面BB1C1C的交线PM∥ED,连结EM,易证MP=ED,∴MP綊ED,则M到达B1时仍可构成四边形,即P到F.而P在C1F之间,不满足要求.P到点C1仍可构成四边形.二、填空题6.平面α、β相交,在α、β内各取两点,这四点都不在交线上,这四点能确定________个平面.解析:若过四点中任意两点的连线与另外两点的连线相交或平行,则确定一个平面;否则确定四个平面.答案:1或47.(2012·宁德质检)在空间中,①若四点不共面,则这四点中任何三点都不共线;②若两条直线没有公共点,则这两条直线是异面直线.以上两个命题中,逆命题为真命题的是__________(把符合要求的命题序号都填上).解析:对于①可举反例,如AB∥CD,A、B、C、D没有三点共线,但A、B、C、D共面.对于②由异面直线定义知正确,故填②.答案:②8.如图,ABCD-A1B1C1D1是长方体,AA1=a,∠BAB1=∠B1A1C1=30°,则AB与A1C1所成的角为________,AA1与B1C所成的角为________.解析: AB∥A1B1,∴∠B1A1C1是AB与A1C1所成的角,∴AB与A1C1所成的角为30°. AA1∥BB1,∴∠BB1C是AA1与B1C所成的角,由已知条件可以得出BB1=a,AB1=A1C1=2a,AB=a,∴B1C1=BC=a.∴BB1C1C是正方形,∴∠BB1C=45°.答案:30°45°三、解答题9.如图,空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD上的点,请回答下列问题:(1)满足什么条件时,四边形EFGH为平行四边形?(2)满足什么条件时,四边形EFGH为矩形?(3)满足什么条件时,四边形EFGH为正方形?解:(1)E、F、G、H为所在边的中点时,四边形EFGH为平行四边形.证明如下: E、H分别是AB、AD的中点,∴EH∥BD,且EH=BD.同理,FG∥BD,且FG=BD,从而EH∥FG,且EH=FG,所以四边形EFGH为平行四边形.(本题答案不唯一,只要保证平面EFGH与AC、BD都平行,则EFGH就为平行四边形.)(2)当E、F、G、H为所在边的中点且BD⊥AC时,四边形EFGH为矩形.(3)当E、F、G、H为所在边的中点且BD⊥AC,AC=BD时,四边形EFGH为正方形.10.如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC綊AD,BE綊FA,G、H分别为FA、FD的中点.(1)证明:四边形BCHG是平行四边形;(2)C、D、F、E四点是否共面?为什么?解:(1)证明:由题设知,FG=GA,FH=HD,所以GH∥AD且GH=AD.又BC∥AD且BC=AD,故GH綊BC.所以四边形BCHG是平行四边形.(2)C、D、F、E四点共面.理由如下:由BE綊AF,G是FA的中点知,BE綊GF,所以EF∥BG.由(1)知BG∥CH,所以EF∥CH,故EC、FH共面.又点D在...