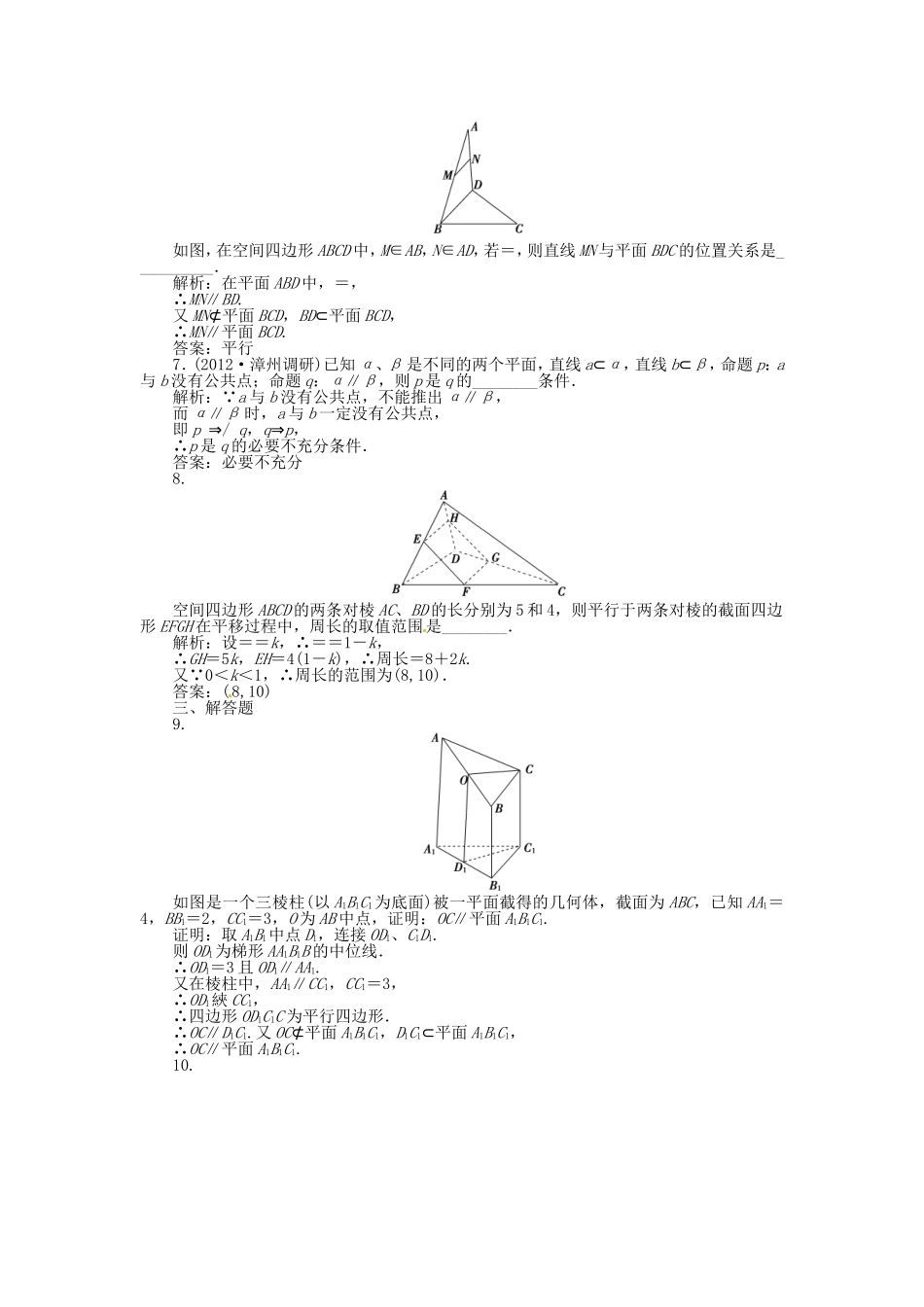
一、选择题1.一条直线若同时平行于两个相交平面,则这条直线与这两个平面的交线的位置关系是()A.异面B.相交C.平行D.不确定解析:选C.以四棱柱为模型,一条侧棱与和它平行的两个侧面的交线平行,可得出结论.2.设m,n是平面α内的两条不同直线;l1,l2是平面β内的两条相交直线.则α∥β的一个充分而不必要条件是()A.m∥β且l1∥αB.m∥l1且n∥l2C.m∥β且n∥βD.m∥β且n∥l2解析:选B. m∥l1,且n∥l2,又l1与l2是平面β内的两条相交直线,∴α∥β,而当α∥β时不一定推出m∥l1且n∥l2,可能异面.故选B.3.(2012·宁德调研)已知甲命题:“如果直线a∥b,那么a∥α”;乙命题:“如果a∥平面α,那么a∥b”.要使上面两个命题成立,需分别添加的条件是()A.甲:b⊂α;乙:b⊂αB.甲:b⊂α;乙:a⊂β且α∩β=bC.甲:a⊄α,b⊂α;乙:a⊂β且α∩β=bD.甲:a⊄α,b⊂α;乙:b∥α解析:选C.根据直线与平面平行的判定定理和性质定理,知C正确.4.下列命题中正确的个数是()①若直线a不在α内,则a∥α;②若直线l上有无数个点不在平面α内,则l∥α;③若直线l与平面α平行,则l与α内的任意一条直线都平行;④如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行;⑤若l与平面α平行,则l与α内任何一条直线都没有公共点;⑥平行于同一平面的两直线可以相交.A.1B.2C.3D.4解析:选B.a∩α=A时,a⊄α,故①错;直线l与α相交时,l上有无数个点不在α内,故②错;l∥α时,α内的直线与l平行或异面,故③错;a∥b,b∥α时,a∥α或a⊂α,故④错;l∥α,l与α无公共点,∴l与α内任一直线都无公共点,⑤正确;长方体中A1C1与B1D1都与面ABCD平行,∴⑥正确.故选B.5.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是()A.①③B.①④C.②③D.②④解析:选B.对图①,可通过面面平行得到线面平行.对图④,通过证明AB∥PN得到AB∥平面MNP,故选B.二、填空题6.如图,在空间四边形ABCD中,M∈AB,N∈AD,若=,则直线MN与平面BDC的位置关系是__________.解析:在平面ABD中,=,∴MN∥BD.又MN⊄平面BCD,BD⊂平面BCD,∴MN∥平面BCD.答案:平行7.(2012·漳州调研)已知α、β是不同的两个平面,直线a⊂α,直线b⊂β,命题p:a与b没有公共点;命题q:α∥β,则p是q的________条件.解析: a与b没有公共点,不能推出α∥β,而α∥β时,a与b一定没有公共点,即p⇒/q,q⇒p,∴p是q的必要不充分条件.答案:必要不充分8.空间四边形ABCD的两条对棱AC、BD的长分别为5和4,则平行于两条对棱的截面四边形EFGH在平移过程中,周长的取值范围是________.解析:设==k,∴==1-k,∴GH=5k,EH=4(1-k),∴周长=8+2k.又 0<k<1,∴周长的范围为(8,10).答案:(8,10)三、解答题9.如图是一个三棱柱(以A1B1C1为底面)被一平面截得的几何体,截面为ABC,已知AA1=4,BB1=2,CC1=3,O为AB中点,证明:OC∥平面A1B1C1.证明:取A1B1中点D1,连接OD1、C1D1.则OD1为梯形AA1B1B的中位线.∴OD1=3且OD1∥AA1.又在棱柱中,AA1∥CC1,CC1=3,∴OD1綊CC1,∴四边形OD1C1C为平行四边形.∴OC∥D1C1.又OC⊄平面A1B1C1,D1C1⊂平面A1B1C1,∴OC∥平面A1B1C1.10.已知如图:E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.求证:(1)EG∥平面BB1D1D;(2)平面BDF∥平面B1D1H.证明:(1)取B1D1的中点O,连接GO,OB,易证四边形BEGO为平行四边形,故OB∥GE,由线面平行的判定定理即可证EG∥平面BB1D1D.(2)由正方体得BD∥B1D1.如图,连接HB、D1F,易证四边形HBFD1是平行四边形,故HD1∥BF.又B1D1∩HD1=D1,BD∩BF=B,所以平面BDF∥平面B1D1H.一、选择题1.(2012·三明调研)如图所示,在三棱柱ABCA′B′C′中,点E、F、H、K分别为AC′、CB′、A′B、B′C′的中点,G为△ABC的重心,从K、H、G、B′中取一点作为P,使得该棱柱恰有2条棱与平面PEF平行,则P为()A.KB.HC.GD.B′解析:选C.若K点为P, P(K)F∥C′C,∴P(K)F∥C′C∥A′A∥B′B,则棱柱至少有三条棱与平...