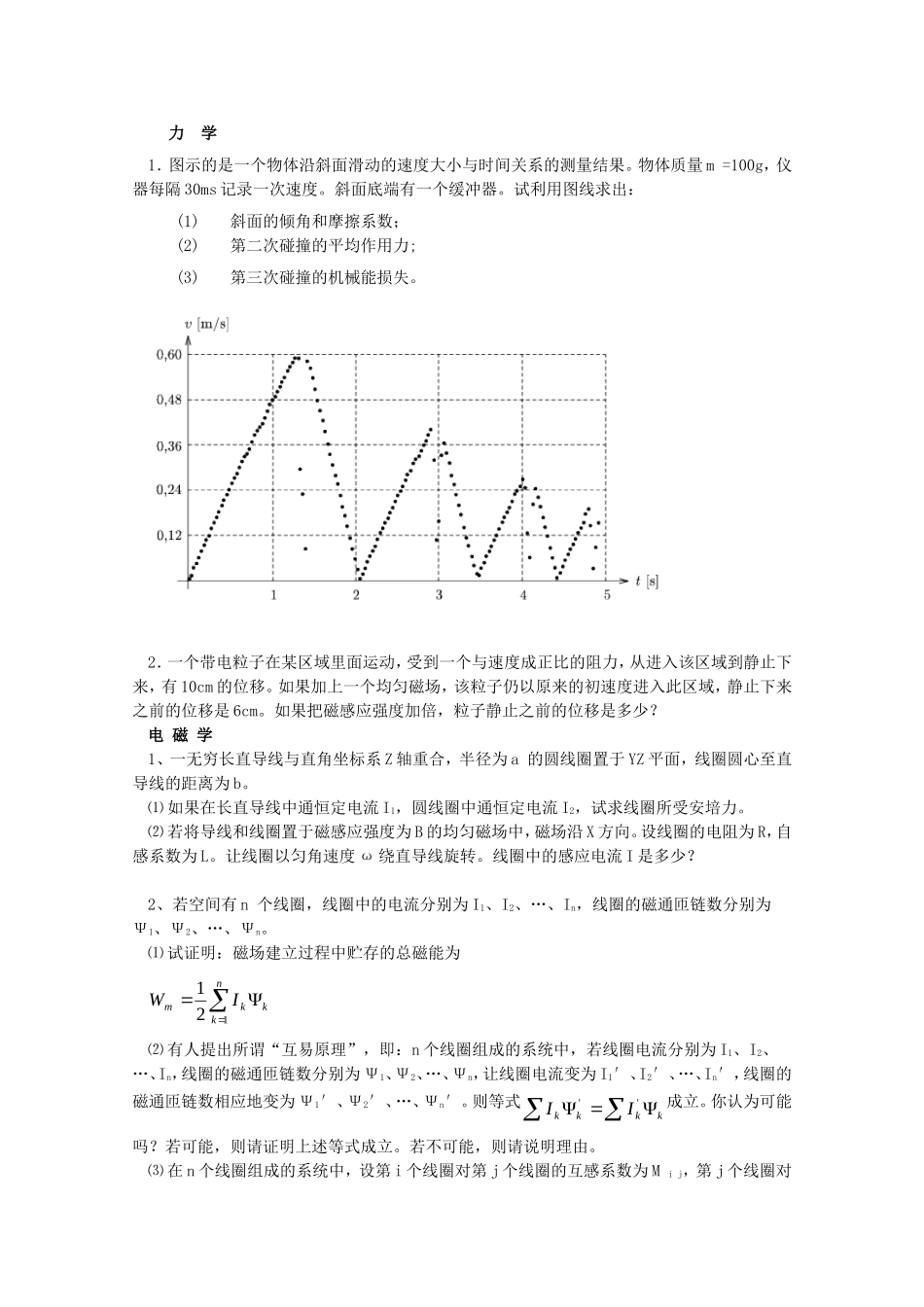
力学1.图示的是一个物体沿斜面滑动的速度大小与时间关系的测量结果。物体质量m=100g,仪器每隔30ms记录一次速度。斜面底端有一个缓冲器。试利用图线求出:(1)斜面的倾角和摩擦系数;(2)第二次碰撞的平均作用力;(3)第三次碰撞的机械能损失。2.一个带电粒子在某区域里面运动,受到一个与速度成正比的阻力,从进入该区域到静止下来,有10cm的位移。如果加上一个均匀磁场,该粒子仍以原来的初速度进入此区域,静止下来之前的位移是6cm。如果把磁感应强度加倍,粒子静止之前的位移是多少?电磁学1、一无穷长直导线与直角坐标系Z轴重合,半径为a的圆线圈置于YZ平面,线圈圆心至直导线的距离为b。⑴如果在长直导线中通恒定电流I1,圆线圈中通恒定电流I2,试求线圈所受安培力。⑵若将导线和线圈置于磁感应强度为B的均匀磁场中,磁场沿X方向。设线圈的电阻为R,自感系数为L。让线圈以匀角速度ω绕直导线旋转。线圈中的感应电流I是多少?2、若空间有n个线圈,线圈中的电流分别为I1、I2、…、In,线圈的磁通匝链数分别为Ψ1、Ψ2、…、Ψn。⑴试证明:磁场建立过程中贮存的总磁能为nkkkmIW121⑵有人提出所谓“互易原理”,即:n个线圈组成的系统中,若线圈电流分别为I1、I2、…、In,线圈的磁通匝链数分别为Ψ1、Ψ2、…、Ψn,让线圈电流变为I1′、I2′、…、In′,线圈的磁通匝链数相应地变为Ψ1′、Ψ2′、…、Ψn′。则等式kkkkII''成立。你认为可能吗?若可能,则请证明上述等式成立。若不可能,则请说明理由。⑶在n个线圈组成的系统中,设第i个线圈对第j个线圈的互感系数为Mij,第j个线圈对第i个线圈的互感系数为Mji,试证明:Mij=Mji。光学对光学成像系统定义入射光所在的空间为物空间出射光所在的空间为像空间。现有一个半径为R的介质透明球,折射率为n,置于空气(折射率为n空)和水(折射率为n水)分界面上,如图,光线从空气入射,如仅考虑图中球面轴线附近的部分。求1)该系统的物空间焦距(即点光源放在此点出射光为平行光)和像空间焦距(及平行光入射出射光的汇聚点)。2)入射光符合什么条件可以使得出射光于入射光平行。3)物放在什么位置,像的大小和方向于物相同。4)物置于入射面前面2R处,像的大小。本题参数R=10cm,n=1.5n水=1.3n空=1.0解题时请先得到代数式,最后带入参数。n空气nn水分界面热学1.一个质量为m=200.0kg,高h=2.00m的薄底大金属桶倒扣在宽广的水池底部(如图)。桶内横截面积S=0.500m2,桶壁和桶底的总体积为V0=2.50×10-2m3,桶内封有高l0=0.200m的空气。池深H0=20.0m,大气压为P0=1atm,水的密度ρ=1.00×103kg/m3,重力加速度为g=9.80m/s2。若用图中吊绳将桶上提使桶底达到水面处,绳拉力所需作的功有一最小值,求这最小功。设水温均匀且不变,水的阻力可忽略,并可忽略水的饱和蒸气压的影响。{本题不提供积分公式。}2.考虑底面积为1m2的无限高空气柱。假设柱内空气温度均匀,空气平均摩尔质量和重力加速度都不随高度变化.它们的值分别为μ=28.9×10-3kg和g=9.80m/s2,且空气可看作双原子理想气体。空气柱底部压强为1atm。求整个空气柱的热容。附:d〔ex(x-1)〕/dx=xex近代物理1.光子和自由电子碰撞的康普顿散射能产生频率更低的散射光,光子和高能的相对论性电子碰撞能产生频率更高的散射光,称为逆康普顿效应。SLAC(StanfordLinearAcceleratorCenter)用以下的方案产生高能单色光子:激光(可见光区)与E=20GeV的电子束对撞。已知电子的静能为0.511MeV,hc=1240eVnm.可见光的典型波长为500nm.(1)求散射光子束的能量和散射角的关系。(2)求散射光子的最大能量近似值(用GeV表示)和它的方向,以及它的波长。(3)散射光子的半数集中在一个立体角内,该立体角的半顶角约为多少?提示:在一个电子和一个光子的质心参考系可以认为散射光子是各向同性的,即半数光子的立体角的半顶角是90度。2.设两惯性系A和B,在t=0时坐标重合,B相对于A以速度V(并不平行于x轴)匀速运动,试导出位置矢量r(其分量为x,y,z)与时间t从A系到B系的洛仑兹变换公式,并将结果写成矢量形式。(提示:把r分解为平行于V的分量与垂直V于的分量,并利用洛仑兹变换)