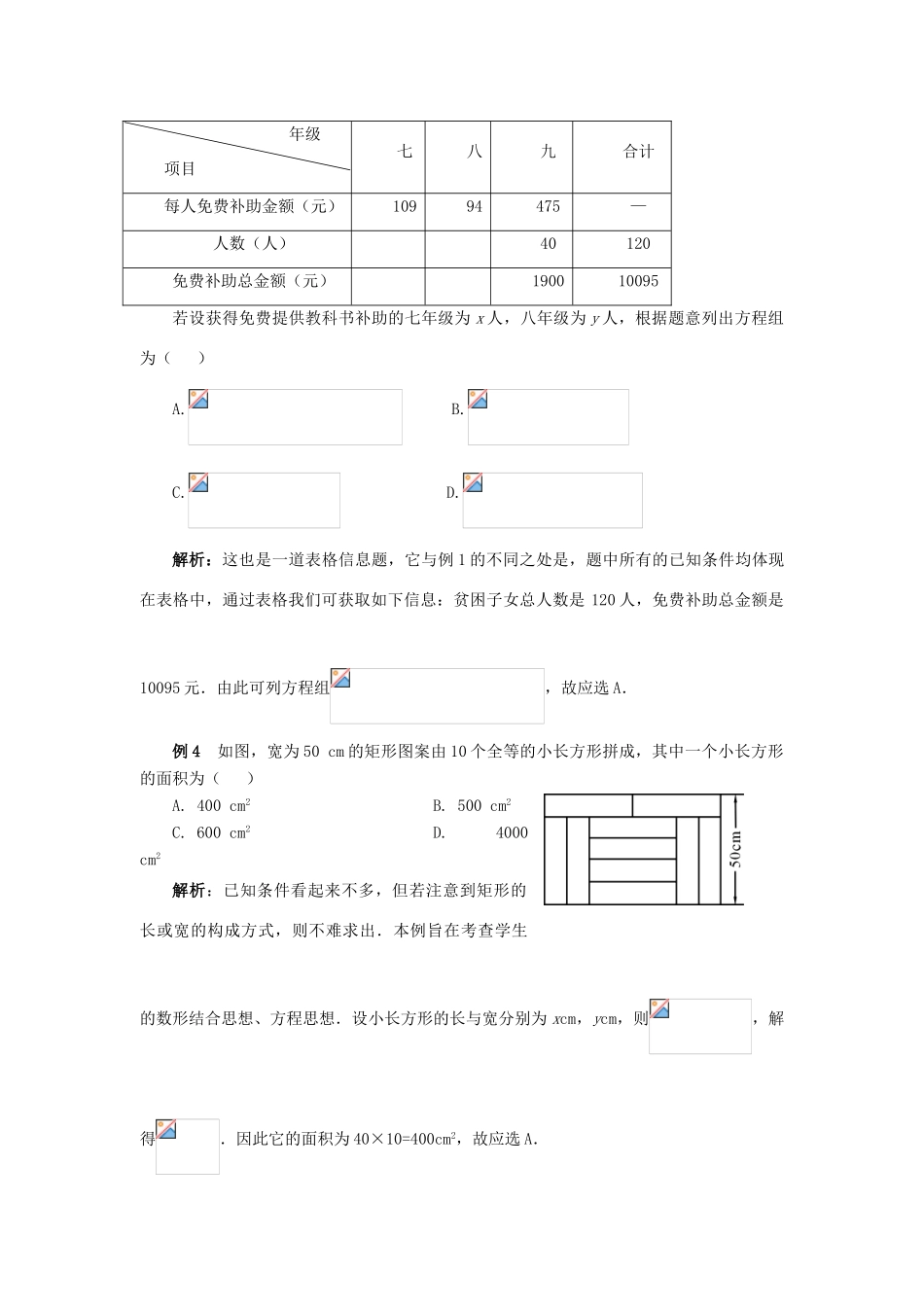
第七章二元一次方程组选择题赏析在中考试题中,多样化的二元一次方程组选择题成为一大亮点,现举例说明.例1某校初三(2)班40名同学为“希望工程”捐款,共捐款100元.捐款情况如表:捐款(元)1234人数67表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.若设捐款2元的有x名同学,捐款3元的有y名同学,根据题意,可得方程组()A.B.C.D.解析:这是一道表格信息题,通过已知条件可发现两个等量关系:总人数为40人,总捐款金额100元.利用表格信息可列方程组,故应选A.例2如图,点O在直线AB上,OC为射线,比的3倍少,设,的度数分别为,,那么下列求出这两个角的度数的方程是()A.B.C.D.解析:本题侧重考查学生的数形结合思想.已知条件看似给了一个,其实还有一个隐含条件,即与互为邻补角.利用它们可列方程组,故应选B.例3为了贫困子女能完成初中学业,国家给他们免费提供教科书,下表是某中学免费提供教科书的补助的部分情况:CAB12O年级项目七八九合计每人免费补助金额(元)10994475—人数(人)40120免费补助总金额(元)190010095若设获得免费提供教科书补助的七年级为x人,八年级为y人,根据题意列出方程组为()A.B.C.D.解析:这也是一道表格信息题,它与例1的不同之处是,题中所有的已知条件均体现在表格中,通过表格我们可获取如下信息:贫困子女总人数是120人,免费补助总金额是10095元.由此可列方程组,故应选A.例4如图,宽为50cm的矩形图案由10个全等的小长方形拼成,其中一个小长方形的面积为()A.400cm2B.500cm2C.600cm2D.4000cm2解析:已知条件看起来不多,但若注意到矩形的长或宽的构成方式,则不难求出.本例旨在考查学生的数形结合思想、方程思想.设小长方形的长与宽分别为xcm,ycm,则,解得.因此它的面积为40×10=400cm2,故应选A.例5古代有这样一个寓言故事:驴子和骡子一同走,它们驮着不同袋数的货物,每袋货物都是一样重的.驴子抱怨负担太重,骡子说:“你抱怨干吗?如果你给我一袋,那我所负担的就是你的两倍;如果我给你一袋,我们才恰好驮的一样多!”那么驴子原来所驮货物的袋数是()A.5B.6C.7D.8解析:此题出自于《希腊文集》,曾被大数学家欧拉改编过.通过驴和骡子的对话可知:2(驴驮袋-1)=骡驮袋+1,驴驮袋+1=骡驮袋-1.因此我们可设驴驮x袋,则骡子驮y袋,则,解得.故应选A.