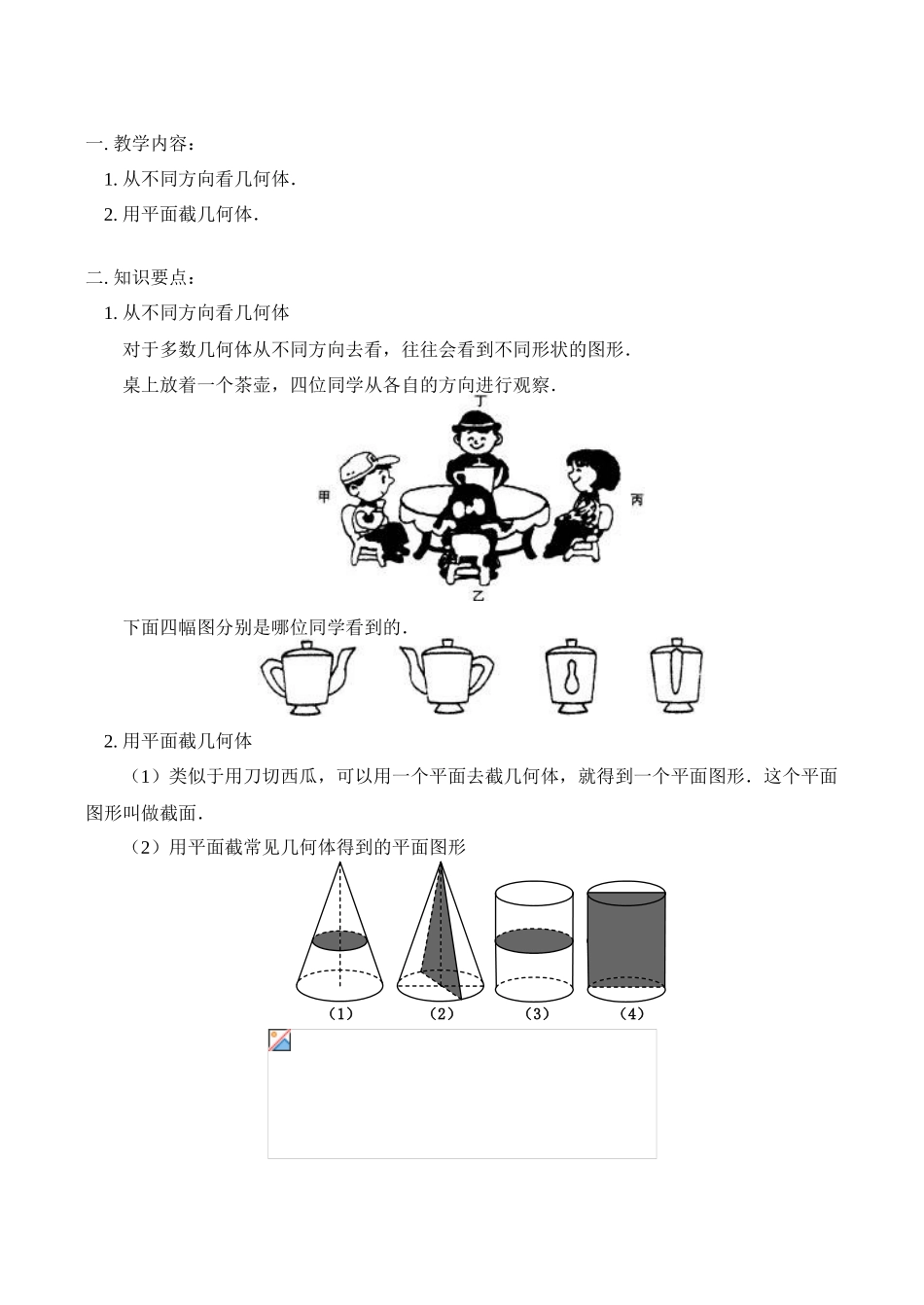
一.教学内容:1.从不同方向看几何体.2.用平面截几何体.二.知识要点:1.从不同方向看几何体对于多数几何体从不同方向去看,往往会看到不同形状的图形.桌上放着一个茶壶,四位同学从各自的方向进行观察.下面四幅图分别是哪位同学看到的.2.用平面截几何体(1)类似于用刀切西瓜,可以用一个平面去截几何体,就得到一个平面图形.这个平面图形叫做截面.(2)用平面截常见几何体得到的平面图形(1)(2)(3)(4)找一个平面截几何体所得截面的方法是:(1)找出平面和几何体的面相交而成的线;(2)判断这些线围成截面的形状.三.重点难点:重点是学会通过从不同方向观察几何体和用平面截几何体,把立体图形问题转化成平面图形来研究.难点是通过分析几何体的三视图想象原几何体的形状.【典型例题】例1.如图所示是从正面、左面、上面看图中的几何体,分别得到的三个平面图形.请指出,这三个平面图形分别是从哪个方向看这个几何体得到的.分析:对于多数几何体从不同的方向去看,往往看到不同形状的图形.这个几何体从三个不同的方向看到了三个不同的图形即视图:从正面看到的叫主视图,从左面看到的叫左视图,从上边看到的叫俯视图.解:(1)是从上面看到的;(2)是从左面看到的;(3)是从正面看到的.例2.(1)观察图(1)~(3),如果分别从正面、左面、上面看这三个几何体,分别得到什么平面图形?(2)对于图(1)和(3)这两个几何体,如果只根据从正面看到的图形,你能把它们区分开吗?(3)对于图(2)和(3)这两个几何体,如果只根据从上面看到的平面图形,你能把它们区分开吗?分析:几何体(1)是长方体,从三个角度看到的平面图形都是长方形;几何体(2)是圆锥,从正面、左面看到的都是等腰三角形,从上面看到的是一个圆形;几何体(3)是圆柱,从正面和左面看到的平面图形都是长方形,从上面看是一个圆形.解:(1)三个几何体三视图分别如图所示.(2)不能区分.因为长方体和圆柱,从正面看,看到的都是长方形.(3)不能区分.因为圆柱和圆锥从上面看都是一个圆.评析:从上面的例子可以看出简单的几何体一般要从三个方向(正面、左面、上面)看,才能将几何体认识清楚.例3(1)下左图是由若干个小正方形所搭成的几何体及从上面看这个几何体所看到的图形,那么从左边看这个几何体时,所看到的几何图形是()(2)如图所示的4个立体图形中,从左边看是长方形的有()个A.0B.1C.2D.3分析:(1)从左边看,有两列,第一列有三行,第二列有一行,应选B.(2)圆柱体从左边看是长方形,圆锥体从左边看是三角形,半球体从左边看是半圆,长方体从左边看是长方形,因此选C.解:(1)B(2)C评析:从不同方向看立体图形,看到的都是它的一个面,是平面图形,被遮去的部分看不到.例4(1)用一个平面去截一个正方体、截面分别是什么形状?(2)用平面去截正方体,能分别截出三角形、三边相等的三角形和梯形吗?①②③④分析:(1)图①中的截面是正方形,其四边分别是正方体的棱长,四个角都是直角;图②中的截面也是正方形;图③中的截面是长方形,其两邻边的长分别是正方体的一个面的边长和对角线长;图④中的截面是长方形.(2)如果用与相邻的三条棱都相交的平面去截正方体可得三角形,如图①②所示;如用图③所示三个顶点的平面截正方体得到三条边都相等的三角形;如用图④所示的平面去截正方体可得梯形.解:(1)四个截面的平面分别是正方形、正方形、长方形、长方形.(2)都能.如图①②截面都是三角形;如图③所得截面是等边三角形;图④的截面是梯形.例5.在手工课上,需要将一个四棱柱形的橡皮泥变成两块四棱柱的橡皮泥,你能做到吗?请说出两种以上的方法.如果要把它变成一个四棱柱和一个三棱柱呢?说说你的方法.分析:四棱柱之所以称为四棱柱是因为它的底面是四边形,因此要把一个四棱柱变成两个四棱柱时不能改变底面的边数,所以可以从中间截.或者在不改变底面边数的情况下,把底面变成两个四边形,所以也可以从上面向下面截,但必须切到底面的一组对边.要把一个四棱柱变成一个四棱柱和一个三棱柱,必须把底面变成一个四边形和一个三角形....