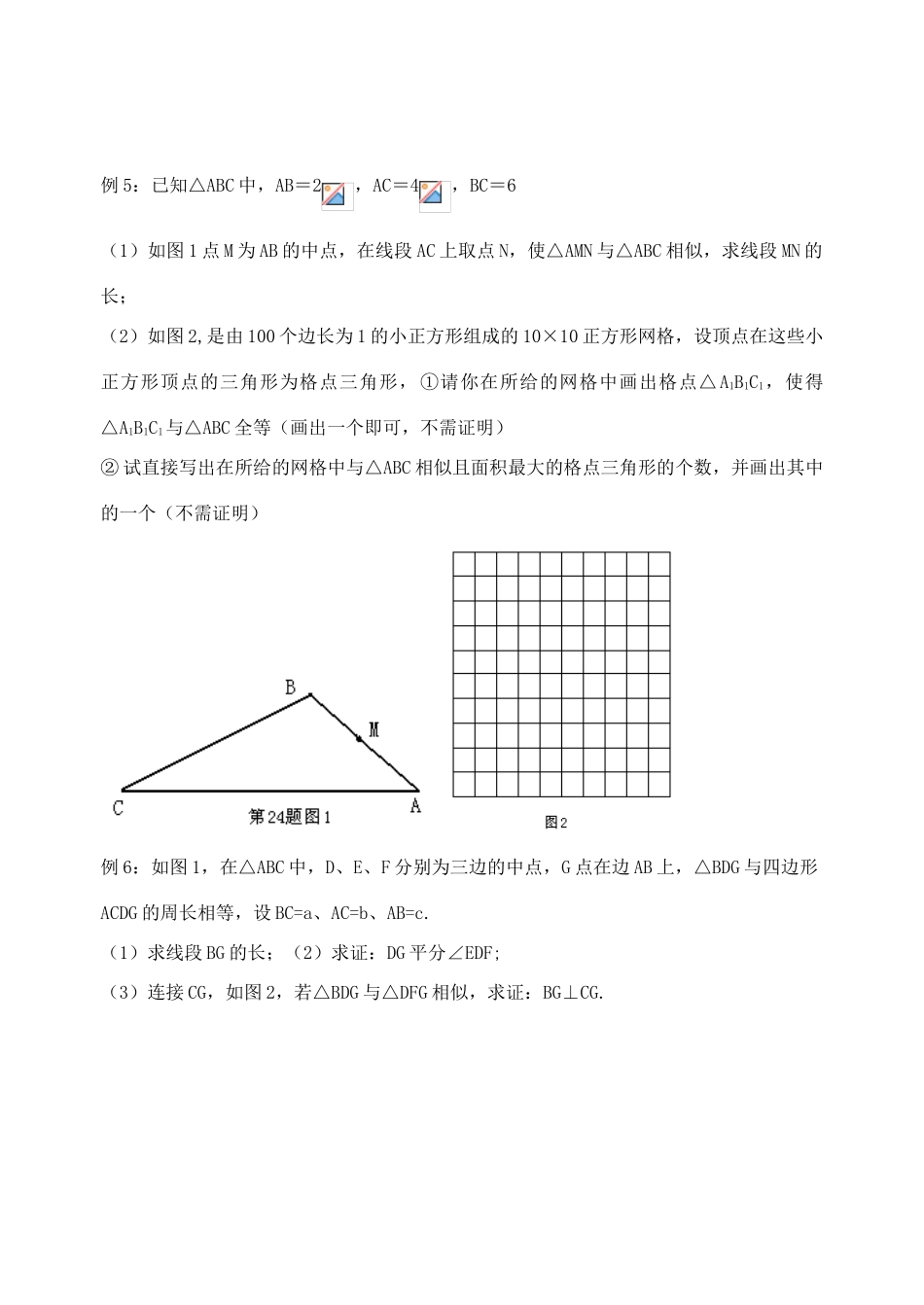
江苏省泰兴市西城中学九年级数学第37课相似新人教版【教学目标】1.了解比例的基本性质,认识图形的相似,理解相似图形的性质。2.了解两个三角形相似的概念,并会利用相似解决相关问题。【教学过程】一.例题讲解例1:已知三个数1,2,,请你再添上一个(只填一个)数,使它们能构成一个比例式,则这个数是_________.例2:如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与相似的是()例3:平面直角坐标系中,如图6,有一条“鱼,它有六个顶点”,则()A.将各点横坐标乘以2,纵坐标不变,得到的鱼与原来的鱼位似B.将各点纵坐标乘以2,横坐标不变,得到的鱼与原来的鱼位似C.将各点横、纵坐标都乘以2,得到的鱼与原来的鱼位似D.将各点横坐标乘以2,纵坐标乘以,得到的鱼与原来的鱼位似例4:正方形边长为4,、分别是、上的两个动点,当点在上运动时,保持和垂直,(1)证明:;(2)设,梯形的面积为,求与之间的函数关系式;当点运动到什么位置时,四边形面积最大,并求出最大面积;(3)当点运动到什么位置时,求此时的值.例5:已知△ABC中,AB=2,AC=4,BC=6(1)如图1点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长;(2)如图2,是由100个边长为1的小正方形组成的10×10正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形,①请你在所给的网格中画出格点△A1B1C1,使得△A1B1C1与△ABC全等(画出一个即可,不需证明)②试直接写出在所给的网格中与△ABC相似且面积最大的格点三角形的个数,并画出其中的一个(不需证明)例6:如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,△BDG与四边形ACDG的周长相等,设BC=a、AC=b、AB=c.(1)求线段BG的长;(2)求证:DG平分∠EDF;(3)连接CG,如图2,若△BDG与△DFG相似,求证:BG⊥CG.泰兴市西城初中初三数学同步训练(37)班级_________学号_________姓名___________成绩_________家长签字__________一.选择题1.三角尺在灯泡的照射下在墙上形成影子(如图所示)。现测得,这个三角尺的周长与它在墙上形成的影子的周长的比是()A.5∶2B.2∶5C.3∶2D.2∶32.如图,在正三角形中,,,分别是,,上的点,,,,则的面积与的面积之比等于()A.1∶3B.2∶3C.∶2D.∶33.已知那么下列各式中一定成立的是()A.B.C.D.二.填空题4.如图,公园内有一个长5米的跷跷板AB,当支点O在距离A端2米时,A端的人可以将B端的人跷高1.5米,那么当支点O在AB的中点时,A端的人下降同样的高度可以将B端的人跷高米.5.锐角△ABC中,BC=6,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为(第1题图)(第2题图)(第4题图)y(y>0),当x=,公共部分面积y最大,y最大值=,三.解答题6.如图,在中,,线段AB的垂直平分线交AB于D,交AC于E,连接BE.(1)求证:∠CBE=36°;(2)求证:.7.如图,在矩形ABCD中,DG⊥AC,垂足为G,若AG=6,CG=12,求矩形ABCD的面积.8.如图,在方格纸中(1)请在方格纸上建立平面直角坐标系,使,并求出点坐标;(2)以原点为位似中心,相似比为2,在第一象限内将放大,画出放大后的图形;(3)计算的面积.9.如图,E是矩形ABCE的边BC上一点,EF⊥AE,EF分别交AC、CD于点M、F,BG⊥AC,垂足为G,BG交AE于点H。(1)求证:△ABE∽△ECF;(2)找出与△ABH相似的三角形,并证明;(3)若E是BC中点,BC=2AB,AB=2,求EM的长。10.△ABC中,∠C=90°,∠A=60°,AC=2cm.长为1cm的线段MN在△ABC的边AB上沿AB方向以1cm/s的速度向点B运动(运动前点M与点A重合).过M、N分别作AB的垂线交直角边于P、Q两点,线段MN运动的时间为ts.(1)若△AMP的面积为y,写出y与t的函数关系式(写出自变量t的取值范围);(2)线段MN运动过程中,四边形MNQP有可能成为矩形吗?若有可能,求出此时tABC(第7题图)的值;若不可能,说明理由;(3)t为何值时,以C、P、Q为顶点的三角形与△ABC相似?