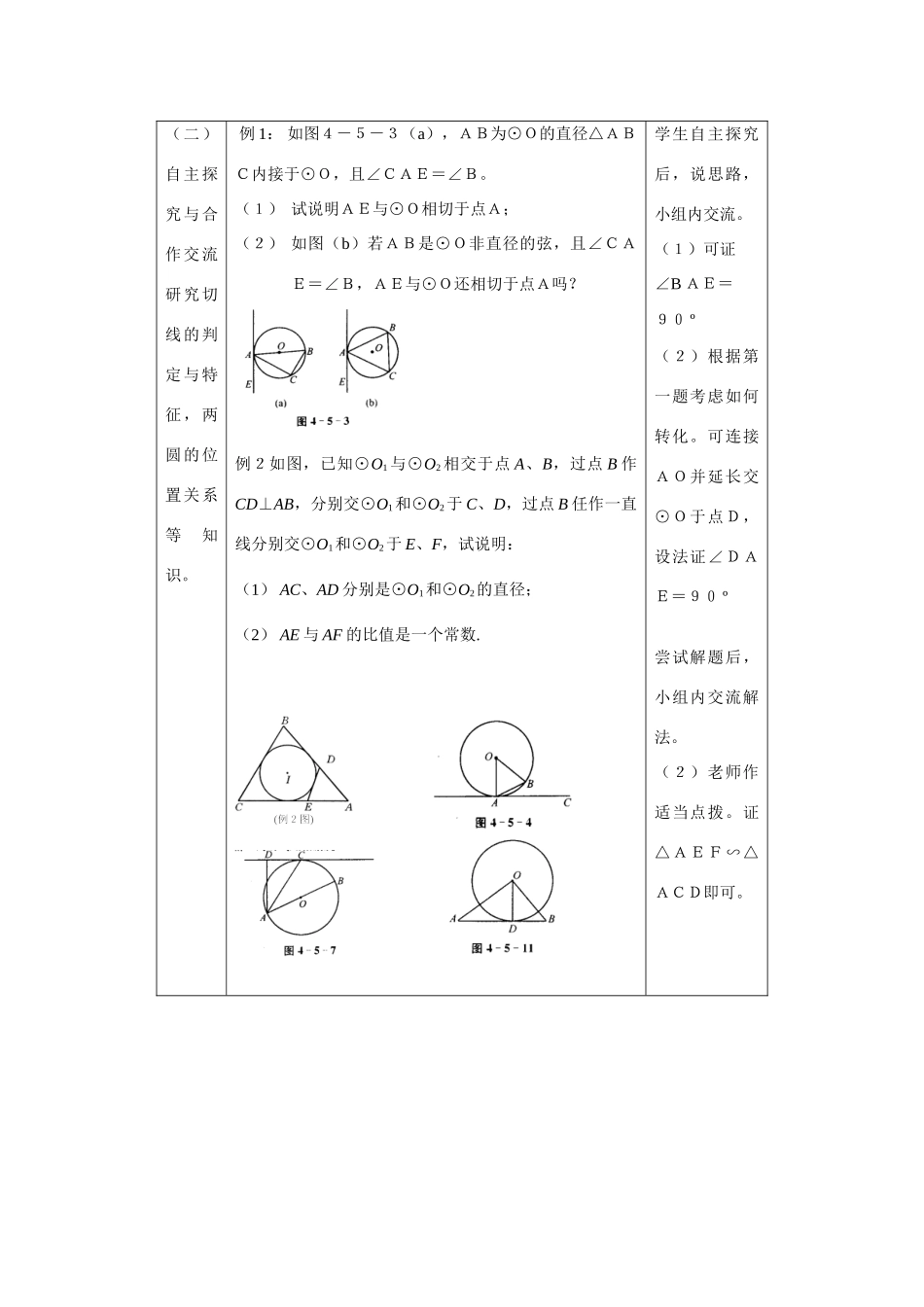
教学内容圆(2)课型复习课课时39执教毛中初三数学组教学目标1、了解三角形的内心与外心,探索并了解直线与圆及圆与圆的位置关系.2、了解圆的切线的概念,掌握切线的判定与特征。会过圆上一点画圆的切线。3、会计算弧长及扇形的面积,会计算圆锥的侧面积和全面积。4、深入理解“转化”、“方程”、“讨论”的数学思想,并培养勇于自主探索,勤于思考的学习习惯,培养团结协调的意识。教学重点目标1、2教学难点目标3教具准备投影仪,胶片.教学过程教师活动学生活动(一)题组探究复习回顾旧知,并知识建构。基础练习:1、下列说法中不正确的是()A、三角形的内心是三角形三条内角平分线的交点。B、锐角三角形、直角三角形、钝角三角形的内心不都在三角形的内部。C、三角形都只有一个外接圆,一个内切圆,反之,圆面积也只有一个内接三角形,外切三角形。D、三角形的内心到三角形的三边距离相等。2、Rt△ABC中,∠ACB=90º,AC=3,BC=4,则以C为圆心,半径为2.4的圆与AB的关系是3、已知⊙A、⊙B相切,圆心距为10cm,其中⊙A的半径为4cm,则⊙B的半径为4、一个扇形的半径为10cm,圆心角为27º,用它做成一个圆锥的侧面,那么圆锥的高为cm5、如图,⊙I是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DEF=50°,则∠A的度数AD=,BE=老师在学生回答的基础上引导总结知识结构,见板书。先回顾旧知,再抢答。并互相补充知识点,进一步完善知识结构。相对应的练习题应指导学生说出相应的知识点及思路。(二)自主探究与合作交流研究切线的判定与特征,两圆的位置关系等知识。例1:如图4-5-3(a),AB为⊙O的直径△ABC内接于⊙O,且∠CAE=∠B。(1)试说明AE与⊙O相切于点A;(2)如图(b)若AB是⊙O非直径的弦,且∠CAE=∠B,AE与⊙O还相切于点A吗?例2如图,已知⊙O1与⊙O2相交于点A、B,过点B作CD⊥AB,分别交⊙O1和⊙O2于C、D,过点B任作一直线分别交⊙O1和⊙O2于E、F,试说明:(1)AC、AD分别是⊙O1和⊙O2的直径;(2)AE与AF的比值是一个常数.学生自主探究后,说思路,小组内交流。(1)可证∠BAE=90º(2)根据第一题考虑如何转化。可连接AO并延长交⊙O于点D,设法证∠DAE=90º尝试解题后,小组内交流解法。(2)老师作适当点拨。证△AEF∽△ACD即可。(三)应用与拓展达标测评:1、两圆的圆心距d=4,两圆的半径分别是方程x2-5x+6=0的两个根,则两圆的位置关系是2、如图4-5-4,A、B是⊙O上的两点,AC是⊙O的切线,∠B=70º,则∠BAC=3、如图4-5-7AB为⊙O的直径,C为⊙O上的上点,AD于过点C的切线互相垂直,垂足为D。(1)说明AC平分∠DAB(2)若将结论“AC平分∠DAB”作为题目的条件,说明AD与过点C的切线互相垂直。4、如图4-5-11,⊙O的半径为6cm,OD┻AB于D,∠AOD=∠B,AD=12cm,BD=3cm,求证:AB是⊙O的切线。本部分内容作为课堂检测用,时间为15分钟。小组内互批。当时知道结果,有利于学生的学习。5、如果圆锥的底面周长是20π,侧面展开后所得的扇形的圆心角为120°,求该圆锥的侧面积和全面积.(四)小结与作业小结:谈一下你有哪些收获?作业:复习资料上相关题独立思考后请学生谈想法,各抒己见。(五)板书设计课题:圆(2)点与圆例:与圆有关的位直线与圆置关系圆与圆弧长公式:圆的弧长与扇形面积计算扇形面积:S侧:圆锥的侧面积与全面积S全:(六)教后记