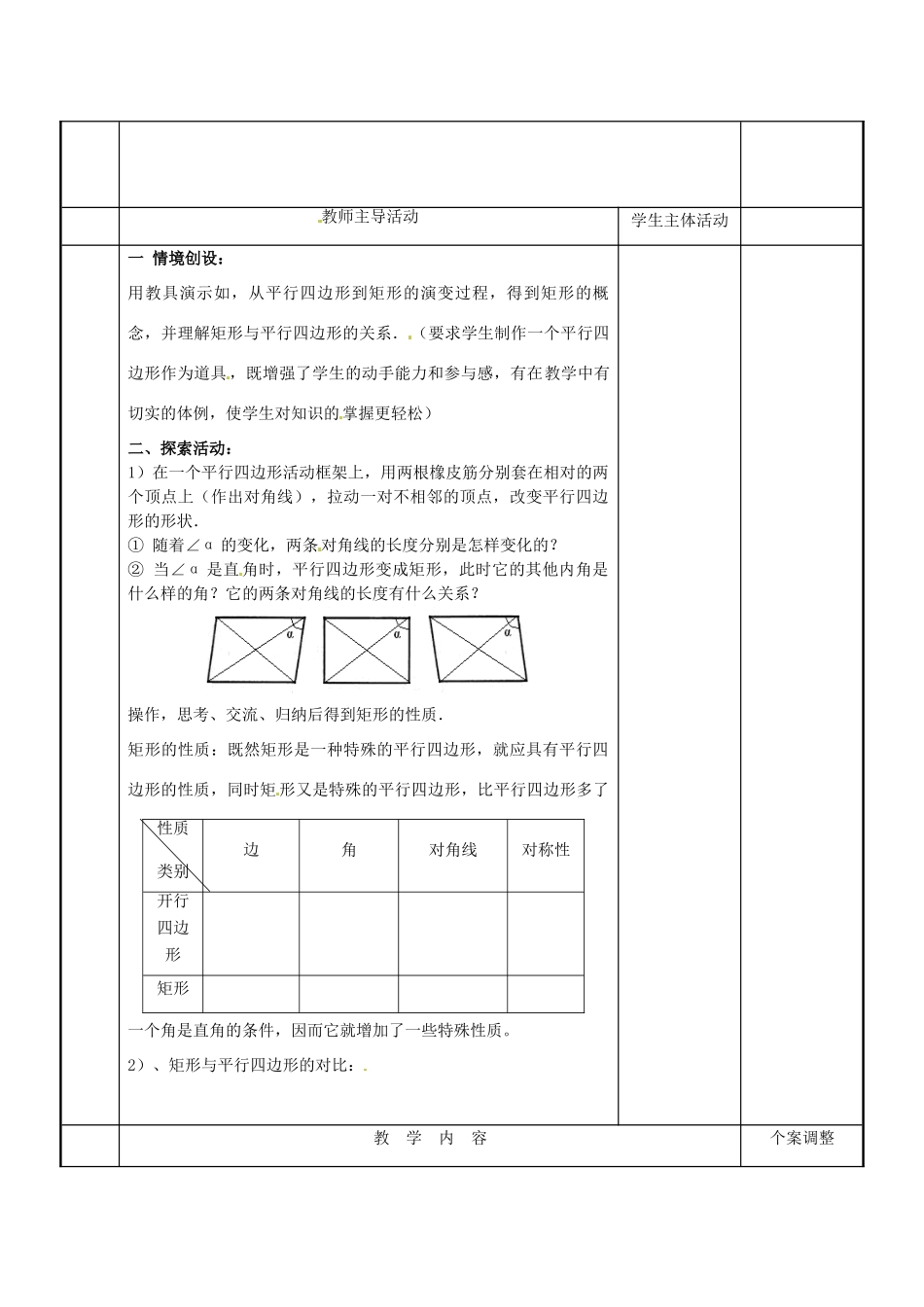
平行四边形、矩形、菱形、正方形的性质和判定(2)主备人用案人授课时间月日总第课时课题课型新授课教学目标1.使学生能应用矩形定义、性质等知识,解决有关问题,进一步培养学生逻辑推理能力。2.能将矩形的性质定理综合应用,激发学生的探索精神重点矩形的性质难点矩形性质定理的综合应用教法及教具讲练结合三角板教学过程教学内容个案调整教师主导活动学生主体活动一情境创设:用教具演示如,从平行四边形到矩形的演变过程,得到矩形的概念,并理解矩形与平行四边形的关系.(要求学生制作一个平行四边形作为道具,既增强了学生的动手能力和参与感,有在教学中有切实的体例,使学生对知识的掌握更轻松)二、探索活动:1)在一个平行四边形活动框架上,用两根橡皮筋分别套在相对的两个顶点上(作出对角线),拉动一对不相邻的顶点,改变平行四边形的形状.①随着∠α的变化,两条对角线的长度分别是怎样变化的?②当∠α是直角时,平行四边形变成矩形,此时它的其他内角是什么样的角?它的两条对角线的长度有什么关系?操作,思考、交流、归纳后得到矩形的性质.矩形的性质:既然矩形是一种特殊的平行四边形,就应具有平行四边形的性质,同时矩形又是特殊的平行四边形,比平行四边形多了一个角是直角的条件,因而它就增加了一些特殊性质。2)、矩形与平行四边形的对比:教学内容个案调整性质类别边角对角线对称性开行四边形矩形教学过程教师主导活动学生主体活动3)如图矩形ABCD,对角线相交于E,图中全等三角形有哪些?准备说说看。将目光锁定在Rt△ABC中,你能看到并想到它有什么特殊的性质吗?现在我们借助于矩形来证明“直角三角形斜边上的中线等于斜边的一半。”三、精讲例题例1如图矩形ABCD的两条对角线相交于点O,且AC=2CD,求证△OCD为正三角形。