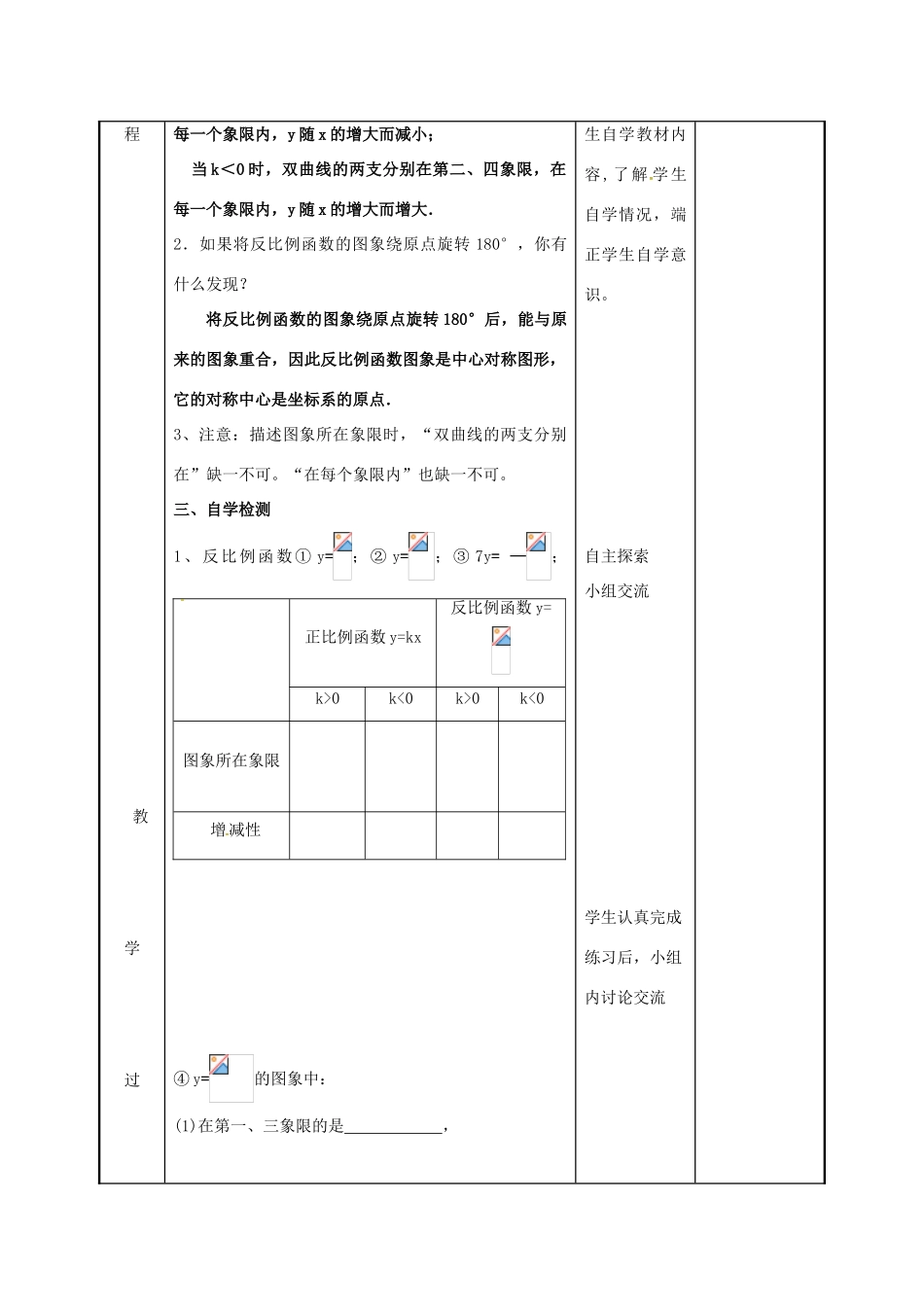
11.2反比例函数的图像与性质教学目标1.认识反比例函数的图象与性质,并能简单运用,根据图象分析并掌握反比例函数的性质,进一步感受数形结合的思想方法2.经历探究反比例函数性质的过程,培养和发展学生的交流、合作和探究能力,提高学生的观察、识图能力,发展学生归纳与概括的能力3.通过对反比例函数图象性质的探究,充分展现了数学的直观形象美,增强学生对数学学习的审美情趣和求知欲重点反比例函数图像的性质及应用难点分析并掌握反比例函数的性质教法教具指导学生解疑释惑检测应用教具:多媒体、课件等教学过教学内容个案调整教师主导活动学生主体活动一、情境引入请画出下列6个反比例函数的图象:y=,y=-,y=,y=-,y=,y=-,请大家进行分类并说明分类的依据,探索图象的特征;(1)每个函数的图象分别在哪几个象限?(2)在每一个象限内,随着x的增大,y是怎样变化的?(3)反比例函数的图象与x轴有交点吗?与y有交点吗?为什么?二、自学指导(一).自学指导1.描点法作反比例函数图像的基本步骤2.反比例函数图像的所在象限3.反比例函数图像的性质(二).自学内容:P129-130反比例函数y=(k为常数,k≠0)的图象是双曲线.当k>0时,双曲线的两支分别在第一、三象限,在回忆交流自主探索小组交流明确要求和目标任务教师巡视,学程教学过每一个象限内,y随x的增大而减小;当k<0时,双曲线的两支分别在第二、四象限,在每一个象限内,y随x的增大而增大.2.如果将反比例函数的图象绕原点旋转180°,你有什么发现?将反比例函数的图象绕原点旋转180°后,能与原来的图象重合,因此反比例函数图象是中心对称图形,它的对称中心是坐标系的原点.3、注意:描述图象所在象限时,“双曲线的两支分别在”缺一不可。“在每个象限内”也缺一不可。三、自学检测1、反比例函数①y=;②y=;③7y=—;④y=的图象中:(1)在第一、三象限的是,生自学教材内容,了解学生自学情况,端正学生自学意识。自主探索小组交流学生认真完成练习后,小组内讨论交流正比例函数y=kx反比例函数y=k>0k<0k>0k<0图象所在象限增减性程在第二、四象限的是(2)在其所在的每一个象限内,y随x的增大而增大的是2.已知反比例函数的图象经过点A(—6,—3).(1)写出函数关系式;(2)这个函数的图象在哪几个象限?y随x的增大怎样变化?(3)点B(4,),C(2,—5)在这个函数的图象上吗?四、展示应用例1已知反比例函数y=的图象经过A(2,-4).求K的值。这个函数的图象在哪几个象限?y随x的增大怎样变化?画出函数的图象。点B(,-16),C(-3,5)在个函数的图象上吗?例2.已知反比例函数y=的图象上有两点P(1,a),Q(b,2.5).(1)求a、b的值;(2)过点P作y轴的垂线交y轴于点M,求△PMO的面积;(3)过点Q作x轴的垂线交x轴于点N,求△QNO的面小组合作完成解:(1)(2)(3)自主探索小组交流教学过程积;(4)过双曲线上任意一点A(m,n)作x轴(或y轴)的垂线,垂足为B,求△ABO的面积;(5)你发现了什么规律?五、当堂反馈1.已知P(1,m+1)在双曲线上,则双曲线在第_________象限,在每个象限y随x的增大而______2.函数y=与y=ax的图象的一个交点A的坐标是(-1,-3),(1)求这两个函数的解析式;(2)在同一直角坐标系内,画出它们的图象;(3)你能求出这两个图象的另一个交点B的坐标吗?六、课堂总结有什么收获?有什么疑惑和遗憾?学生认真完成练习后,小组内讨论交流说说自己的收获与不足板书设计教学札记