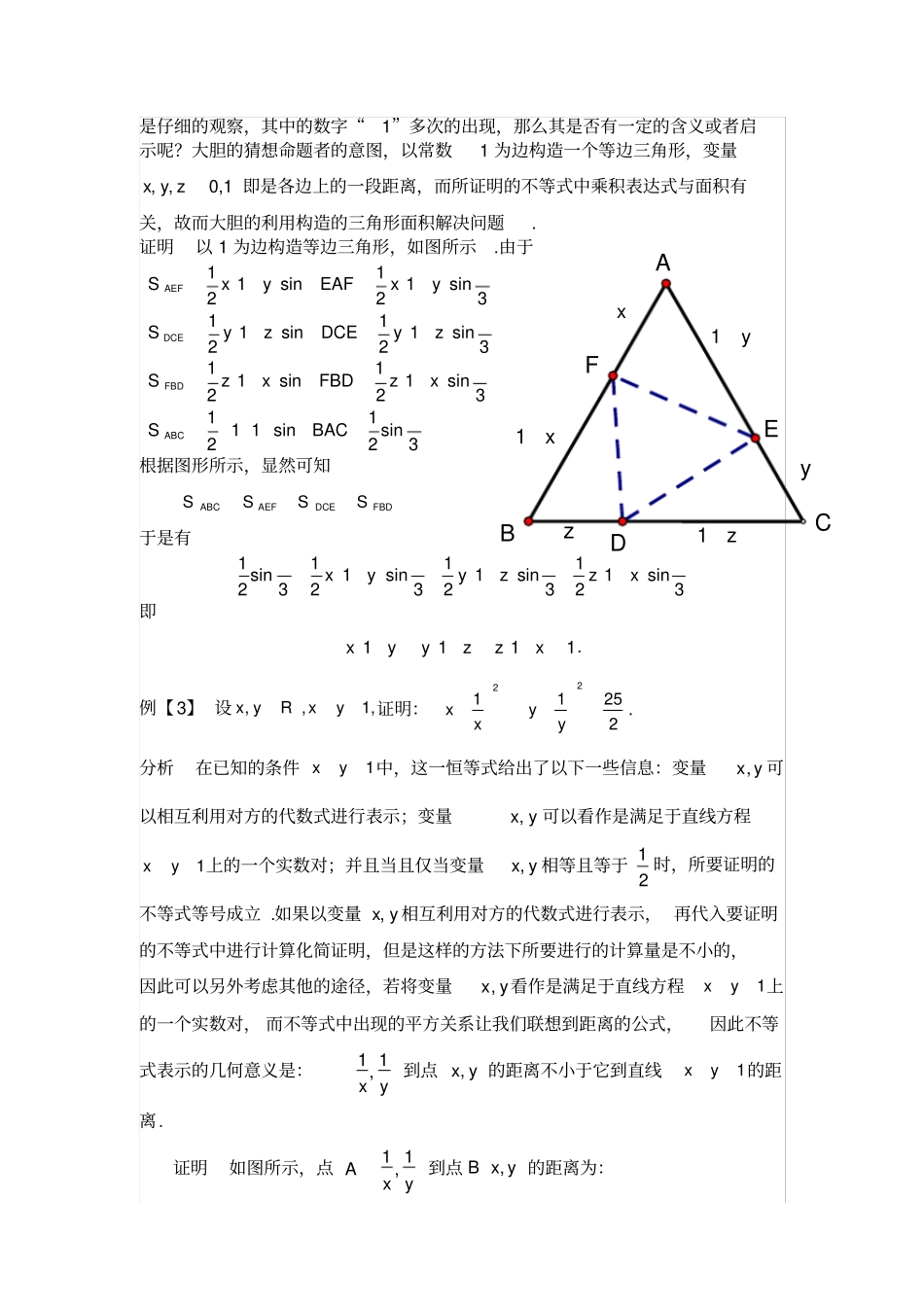
数形结合在不等式证明中的应用数形结合思想简而言之就是把数学中“数”和数学中“形”结合起来解决数学问题的一种数学思想。数形结合具体地说就是将抽象数学语言与直观图形结合起来,使抽象思维与形象思维结合起来,通过“数”与“形”之间的对应和转换来解决数学问题。在中学数学不等式的证明中,主要以“形”助“数”。以“形”助“数”:由于“数”和“形”是一种对应,有些数量比较抽象,我们难以把握,而“形”具有形象,直观的优点,能表达较多具体的思维,起着解决问题的定性作用,因此我们可以把“数”的对应——“形”找出来,利用图形来解决问题。我们能够从所给问题的情境中辨认出符合问题目标的某个熟悉的“模式”,这种模式是指数与形的一种特定关系或结构。这种把数量问题转化为图形问题,并通过对图形的分析、推理最终解决数量问题的方法,就是图形分析法。数量问题图形化是数量问题转化为图形问题的条件,将数量问题转化为图形问题一般有三种途径:应用平面几何知识,应用立体几何知识,应用解析几何知识将数量问题转化为图形问题。解一个数学问题,一般来讲都是首先对问题的结构进行分析,分解成已知是什么(条件),要求得到的是什么(目标),然后再把条件与目标相互比较,找出它们之间的内在联系。因此,对于“数”转化为“形”这类问题,解决问题的基本思路:明确题中所给的条件和所求的目标,从题中已知条件或结论出发,先观察分析其是否相似(相同)于已学过的基本公式(定理)或图形的表达式,再作出或构造出与之相适合的图形,最后利用已经作出或构造出的图形的性质、几何意义等,联系所要求解(求证)的目标去解决问题。中学数学的基本知识分三类:一类是纯粹数的知识,如实数、代数式、方程(组)、不等式(组)、函数等;一类是关于纯粹形的知识,如平面几何、立体几何等;一类是关于数形结合的知识,主要体现是解析几何。数形结合是一个数学思想方法,包含“以形助数”和“以数辅形”两个方面,其应用大致可以分为两种情形:或者是借助形的生动和直观性来阐明数之间的联系,即以形作为手段,数为目的,比如应用函数的图像来直观地说明函数的性质;或者是借助于数的精确性和规范严密性来阐明形的某些属性,即以数作为手段,形作为目的,如应用曲线的方程来精确地阐明曲线的几何性质。数形结合的思想,其实质是将抽象的数学语言与直观的图像结合起来,关键是代数问题与图形之间的相互转化,它可以使代数问题几何化,几何问题代数化。在运用数形结合思想分析和解决问题时,要注意彻底明白一些概念和运算的几何意义以及曲线的代数特征,对数学题目中的条件和结论既分析其几何意义又分析其代数意义。不等式的证明在中学阶段甚至是大学阶段都是很重要的知识模块,其证明的方法也不计其数,但是利用数形结合的方法证明却是其中巧妙便捷的方法之一。下面就以实际例子加以阐述。xyo例【1】已知,,abm都是正数,且ab,求证:aambbm.分析从所要证明的不等式aambbm的结构上观察,其中每一个分式都可以用其对应的几何含义或者代数意义加以“形”化,例如可以联想到三角形相似比的问题、直线斜率的表达等等,因此可以利用数形结合与构造图形的方法进行证明.证明1如右图所示,构造一个直角三角形ABC,在边AC上取一点D,并且使得CDb,过点D作DEBC,垂足为E.令CEa,BEm.由于,CEBCCEBCBCCDADCDCDADCDDF即aamambbADbm证明2根据分式所表达的代数意义将所对应的点在直角坐标系中描出并作出对应的射线和直线,如图所示,由图像及其所在直线的斜率显然可知:aambbm.证明3分析:要证明aambbm成立,即是要证abmbam,不等式两边的乘积表达式不由得会使我们想起矩形的面积(或者是三角形的面积)表达式,以此为据不妨构造以对应因式为边长的矩形.利用图形面积计算证明不等式的正确性.从右边的图形中不难计算出:1223,SSbamSSabm并且可知13,SSab,故而可知1223SSbamSSabm,所以abmbam,于是原不等式aambbm成立.例【2】设,,0,1xyz,求证:1111xyyzzx.分析从题干中能够直接获得信息较少,似乎有很大的困难阻碍证明的进行,但abFEABCDm,ba,mm1S3S2Sabmm是仔细的观察,其中的数字“1”...