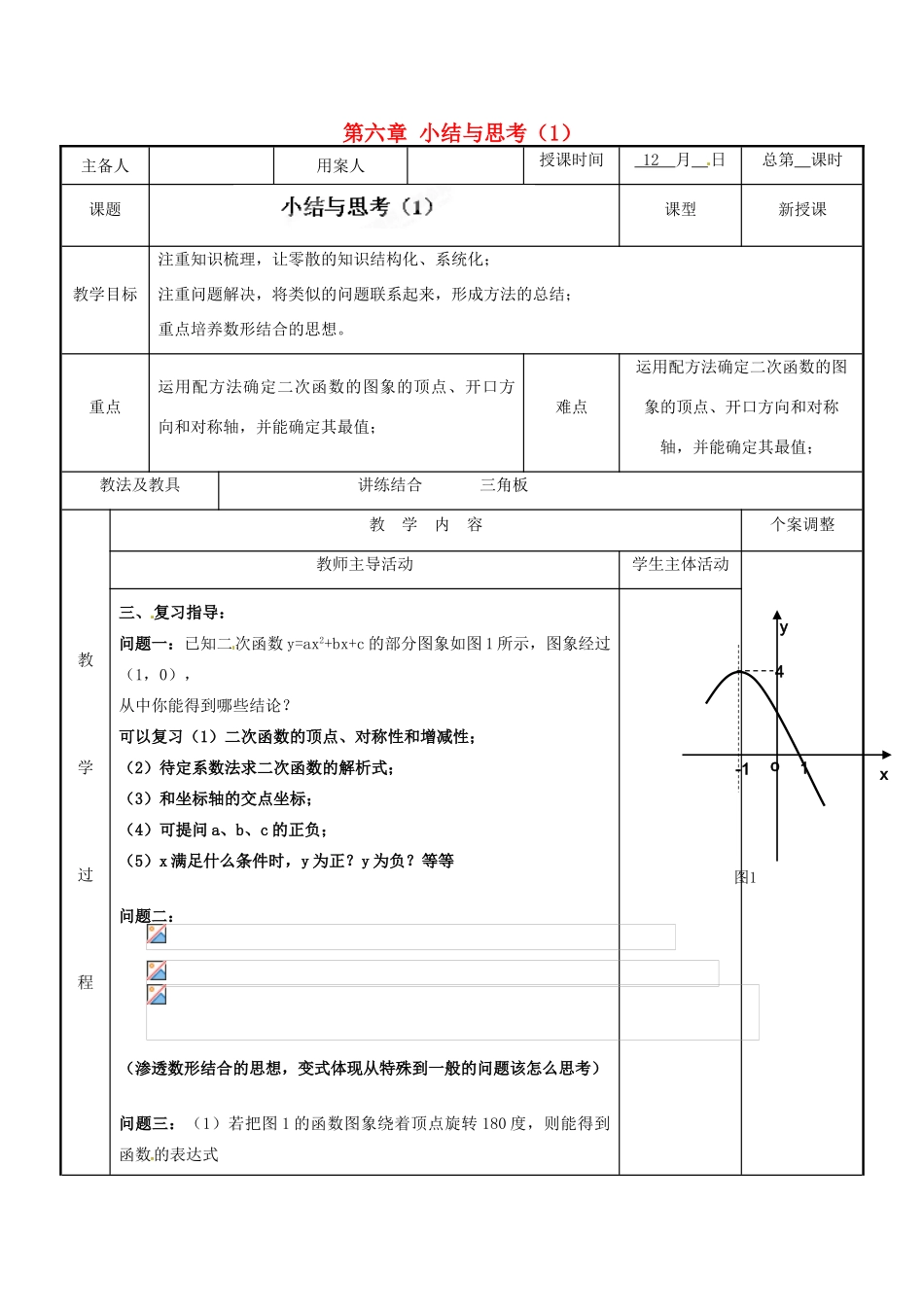
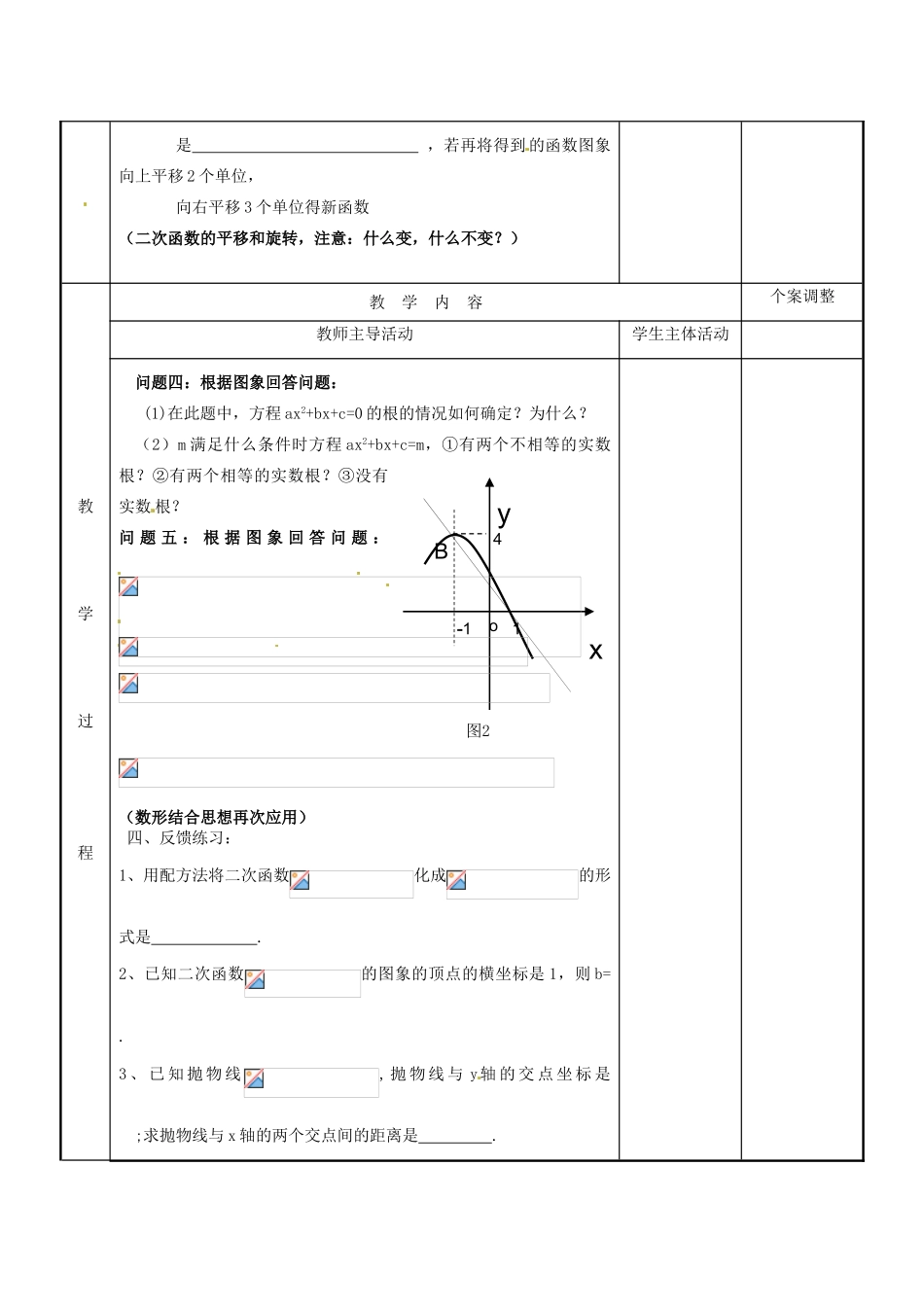
第六章小结与思考(1)主备人用案人授课时间12月日总第课时课题课型新授课教学目标注重知识梳理,让零散的知识结构化、系统化;注重问题解决,将类似的问题联系起来,形成方法的总结;重点培养数形结合的思想。重点运用配方法确定二次函数的图象的顶点、开口方向和对称轴,并能确定其最值;难点运用配方法确定二次函数的图象的顶点、开口方向和对称轴,并能确定其最值;教法及教具讲练结合三角板教学过程教学内容个案调整教师主导活动学生主体活动三、复习指导:问题一:已知二次函数y=ax2+bx+c的部分图象如图1所示,图象经过(1,0),从中你能得到哪些结论?可以复习(1)二次函数的顶点、对称性和增减性;(2)待定系数法求二次函数的解析式;(3)和坐标轴的交点坐标;(4)可提问a、b、c的正负;(5)x满足什么条件时,y为正?y为负?等等问题二:(渗透数形结合的思想,变式体现从特殊到一般的问题该怎么思考)问题三:(1)若把图1的函数图象绕着顶点旋转180度,则能得到函数的表达式xyo4-1图11是,若再将得到的函数图象向上平移2个单位,向右平移3个单位得新函数(二次函数的平移和旋转,注意:什么变,什么不变?)教学过程教学内容个案调整教师主导活动学生主体活动问题四:根据图象回答问题:(1)在此题中,方程ax2+bx+c=0的根的情况如何确定?为什么?(2)m满足什么条件时方程ax2+bx+c=m,①有两个不相等的实数根?②有两个相等的实数根?③没有实数根?问题五:根据图象回答问题:(数形结合思想再次应用)四、反馈练习:1、用配方法将二次函数化成的形式是.2、已知二次函数的图象的顶点的横坐标是1,则b=.3、已知抛物线,抛物线与y轴的交点坐标是;求抛物线与x轴的两个交点间的距离是.Bxyo4-1图21