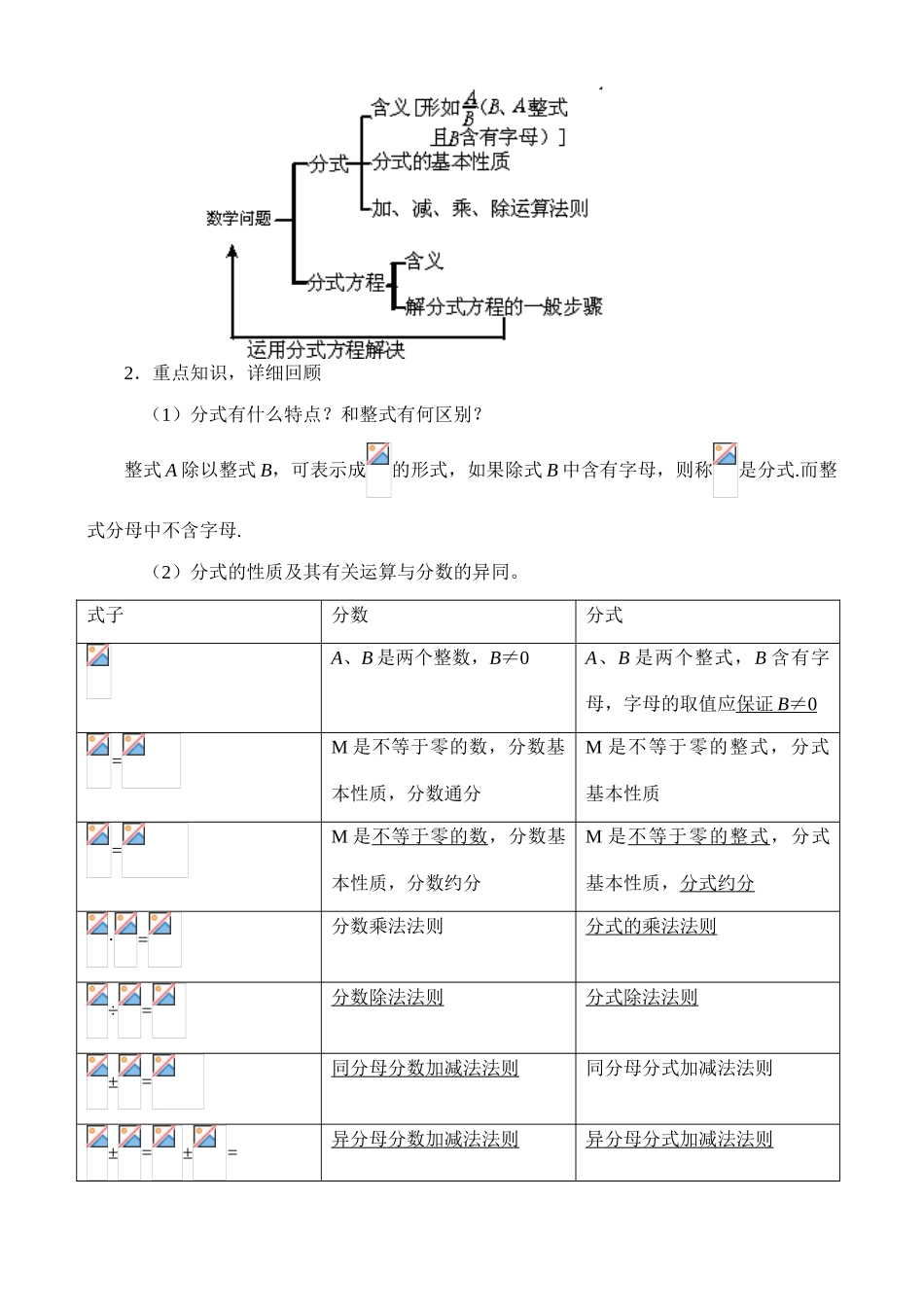
§4.5回顾与思考教学目标1.知识目标:(1)掌握分式的基本性质及分式的有关运算法则.(2)会解分式方程.(3)列分式方程解决实际问题.2.能力目标:通过“类比”与“转化”的思想学习分式的基本性质、分式的运算法则及其分式方程的解法,提高学生思考问题的能力.3.情感目标:通过总结本章内容,培养学生的概括能力.教学重点1.分式的基本性质.2.分式的运算法则.3.分式方程的概念及其解法.4.分式方程的应用.教学难点1.分式的运算及分式方程的解法.2.列分式方程解应用题.教学方法交流讨论法教学过程1.回顾知识,梳理内容本章主要学习了分式的定义,分式的基本性质及有关运算法则,分式的性质及有关运算法则与分数有什么异同,如何解分式方程?它与解一元一次方程有何联系与区别?会列分式方程解决实际生活中的一些问题。如图:2.重点知识,详细回顾(1)分式有什么特点?和整式有何区别?整式A除以整式B,可表示成的形式,如果除式B中含有字母,则称是分式.而整式分母中不含字母.(2)分式的性质及其有关运算与分数的异同。式子分数分式A、B是两个整数,B≠0A、B是两个整式,B含有字母,字母的取值应保证B≠0=M是不等于零的数,分数基本性质,分数通分M是不等于零的整式,分式基本性质=M是不等于零的数,分数基本性质,分数约分M是不等于零的整式,分式基本性质,分式约分·=分数乘法法则分式的乘法法则÷=分数除法法则分式除法法则±=同分母分数加减法法则同分母分式加减法法则±=±=异分母分数加减法法则异分母分式加减法法则(3)解分式方程分三步:第一步,去分母,把分式方程转化为整式方程;第二步,解这个整式方程;第三步,将整式方程的根代入最简公分母,如果使最简公分母为零,则此根为原方程的增根,若最简公分母不为零,则此根是原方程的解.3.变式训练,巩固提高(一)填空(1)某人在外面晨练,有m分钟,他每分钟走a米;有n分钟,他每分钟跑b米.求此人晨练平均每分钟行米?答案:此人晨练时平均每分钟行米.(2)长方形的面积为8m2,长为pm,宽为____________m.答案:m.(3)如果某商品降价x%后的售价为a元,那么该商品的原价为多少元?答案:原价为元(二)计算(1)当x为何值时,下列分式的值为零.①;②.解:①由分子(x-2)(x-3)=0,得x=2或x=3.当x=2时,x2-9≠0;当x=3时,x2-9=0.所以当x=2时,分式的值为零.②由分子x-1=0,得x=1,而当x=1时,分母x+1=1+1=2≠0.所以当x=1时,分式的值为零.(2)化简①;②.解:①==②=-=-(3)计算:①÷(-)②-③---④+++解:①÷(-)=÷=×=②-=-=-=③---=--=--=-=-=0④+++=+++=(-)+(-)+(-)+(-)=-==(三)列方程解应用题(1)某车间加工1200个零件后,采用了新工艺,工效是原来的1.5倍,这样加工同样多的零件就少用10h,采用新工艺前、后每时分别加工多少个零件?解:设采用新工艺前、后每时分别加工x个,1.5x个,根据题意,得=+10解得x=40,1.5x=40×1.5=60.经检验x=40是原方程的根,也符合题意.答:采用新工艺前后每时分别加工40个、60个.(2)农机厂职工到距工厂15千米的生产队检修农机,一部分人骑自行车先走,40分钟后,其余的人乘汽车出发,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度.解:设自行车的速度为x千米/小时,那么汽车的速度为3x千米/小时.根据题意,得=-解得x=15.经检验x=15是这个方程的解.当x=15时,3x=45.答:自行车的速度是15千米/小时,汽车的速度为45千米/小时.(3)某校师生到距离学校20千米的公路旁植树,甲班师生骑自行车先出发45分钟后,乙班的师生乘汽车出发,结果两班师生同时到达。已知汽车的速度是自行车速度的2.5倍,求两种车的速度各是多少?解:设自行车的速度为x千米/时,则汽车的速度为2.5x千米/时,根据题意,得:-=解方程,得x=16经检验x=16是所列方程的解2.5x=16×2.5=40答:自行车的速度是每小时16千米,汽车的速度是每小时40千米。(4)甲、乙两个车工,同时分别车1500个零件,乙改进了生产技术,生产效率提高到甲的3倍。因此比甲少用了20小时完成任务,问他们每小时各车了多少个零件?解:设甲每小时可...