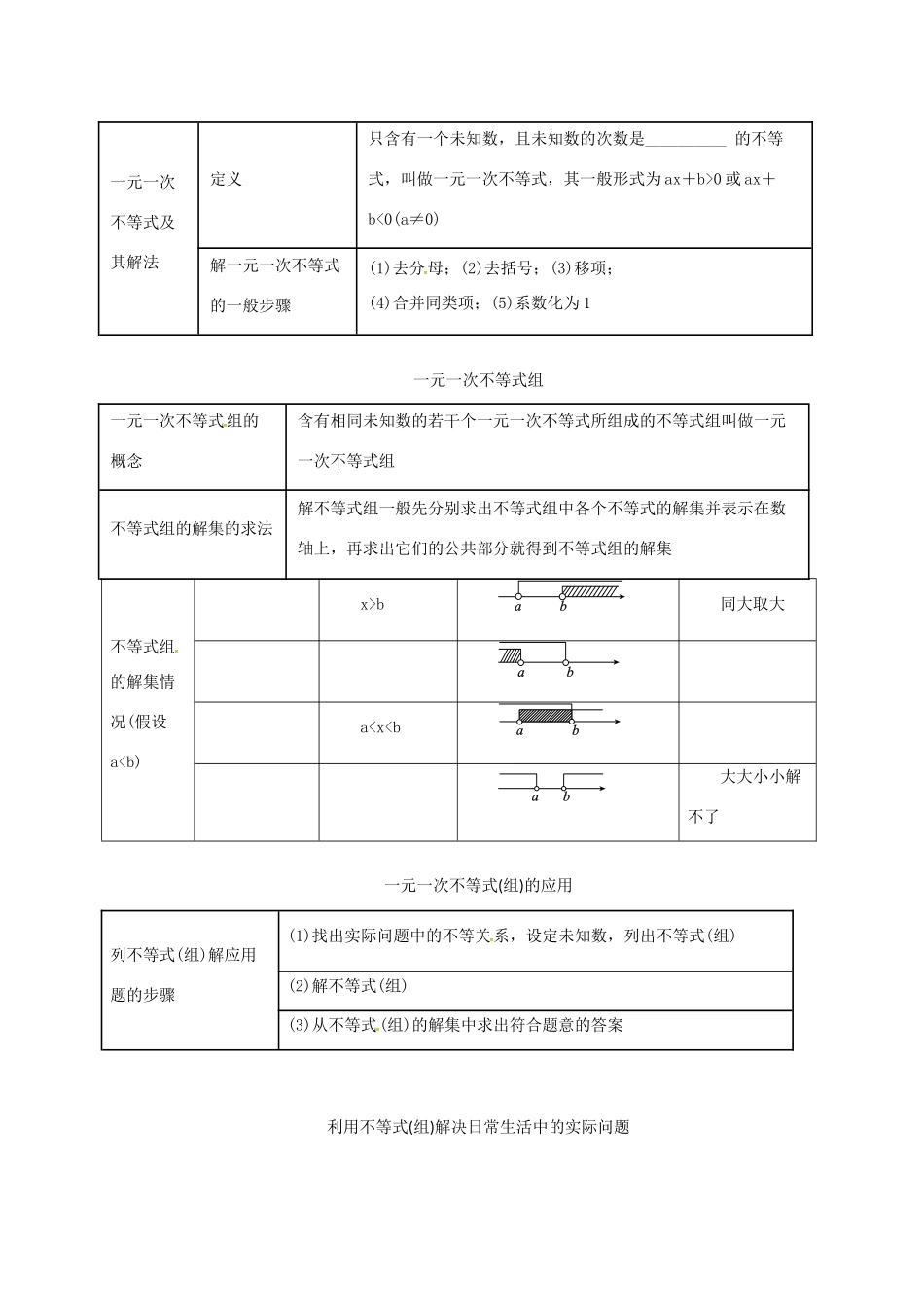
第9讲:一元一次不等式及其应用一、复习目标1、了解一元一次不等式组的概念,会解相应的一元一次不等式组,并把解在数轴上表示。2、掌握一元一次不等式组与二元一次方程组解法上的不同。3、会列相应的一元一次不等式组解实际的应用题,并会结合一次函数的图像及有关性质求实际问题的最优值问题。二、课时安排1课时三、复习重难点1、解一元一次不等式,并将其解在数轴上表示。2、列一元一次不等式组解相应的实际应用题。四、教学过程(一)知识梳理不等式不等式的概念不等式一般地,用_________连接的式子叫做不等式不等式的解使不等式成立的未知数的值叫做不等式的______不等式的解集能使不等式成立的未知数的取值范围叫做不等式的解的集合,简称_________解不等式求不等式解集的过程不等式的基本性质性质1不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向__________性质2不等式两边同乘(或除以)一个正数,不等号的方向________性质3不等式两边同乘(或除以)一个负数,不等号的方向__________一元一次不等式一元一次不等式及其解法定义只含有一个未知数,且未知数的次数是__________的不等式,叫做一元一次不等式,其一般形式为ax+b>0或ax+b<0(a≠0)解一元一次不等式的一般步骤(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)系数化为1一元一次不等式组一元一次不等式组的概念含有相同未知数的若干个一元一次不等式所组成的不等式组叫做一元一次不等式组不等式组的解集的求法解不等式组一般先分别求出不等式组中各个不等式的解集并表示在数轴上,再求出它们的公共部分就得到不等式组的解集不等式组的解集情况(假设ab同大取大ab,则()A.a>-bB.a<-bC.-2a>-2bD.-2a<-2b[解析]由于a、b的取值范围不确定,故可考虑利用特例来说明,A、例如a=0,b=-1,a<-b,故此选项错误,B、例如a=1,b=0,a>-b,故此选项错误,C、利用不等式性质2,同乘以-2,不等号改变,则有-2a<-2b,故此选项错误,由此也说明D选项正确,故选D.点析:(1)运用不等式的性质时,应注意不等式的两边同时乘或者除以一个负数,不等式的方向要改变;(2)生活中的跷跷板、天平等问题,常借助不等式(组)来求解,注意数与形的有机结合.例2、解不等式x-1>2x,并把解集在数轴上表示出来[解析]解不等式一般步骤:去分母,去括号,移项,合并同类项,系数化为1.解:x-2x>1,-x>1,∴x<-2.表示在数轴上为:例3解不等式组:[解析]先分别求出每个不等式的解集,再求出这两个不等式解集的公共部分,就是这个不等式组的解集.解:...