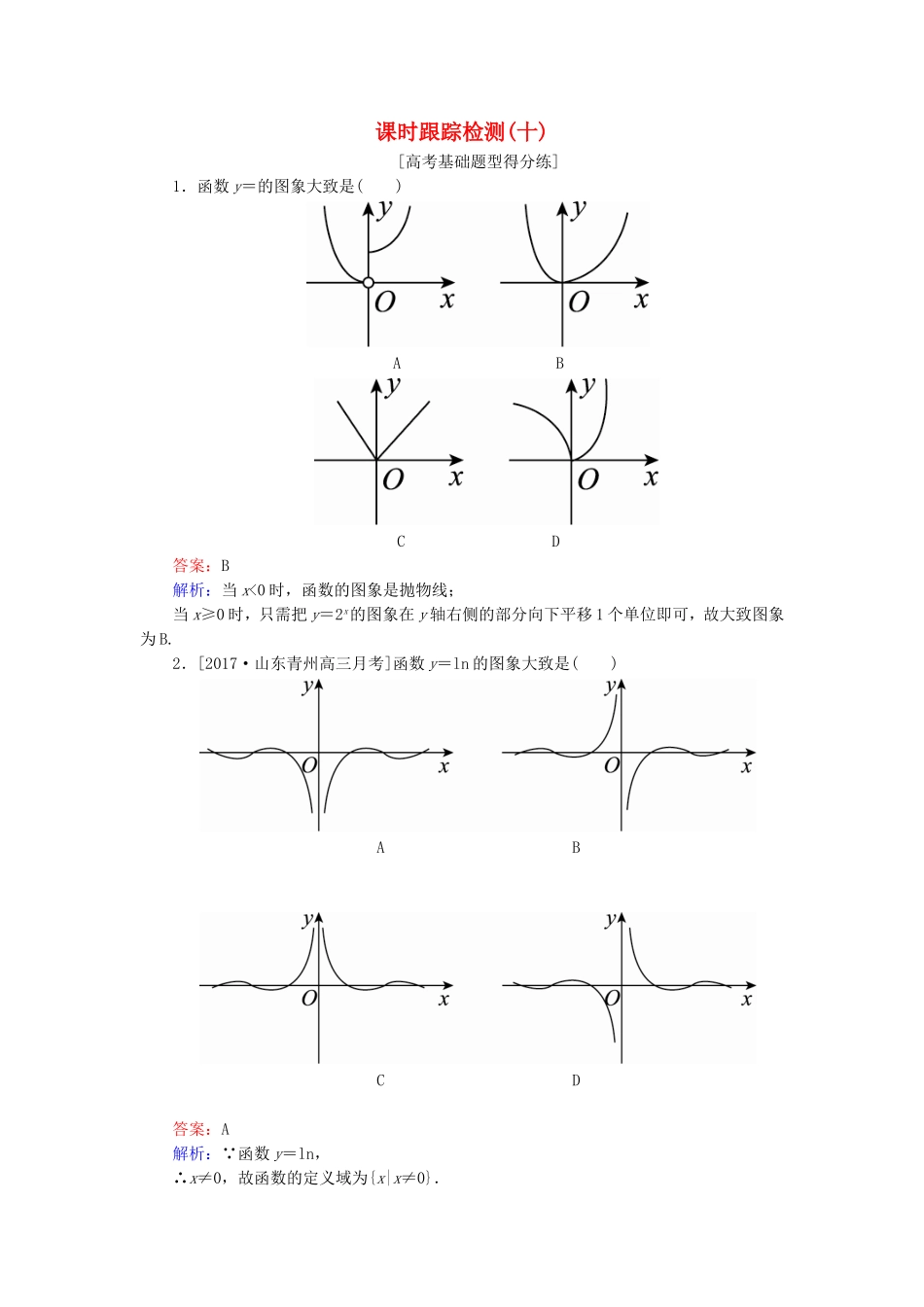
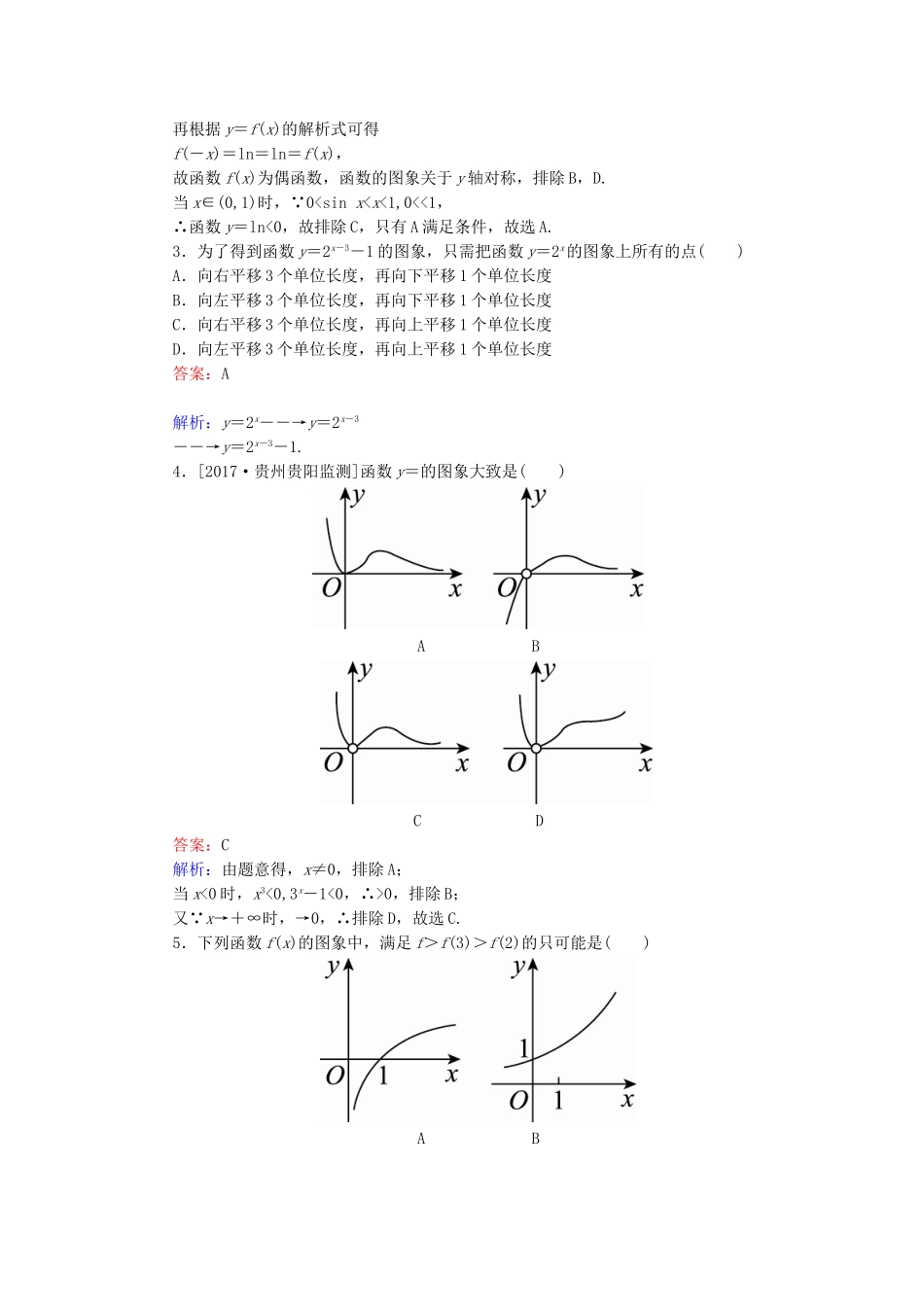
课时跟踪检测(十)[高考基础题型得分练]1.函数y=的图象大致是()ABCD答案:B解析:当x<0时,函数的图象是抛物线;当x≥0时,只需把y=2x的图象在y轴右侧的部分向下平移1个单位即可,故大致图象为B.2.[2017·山东青州高三月考]函数y=ln的图象大致是()ABCD答案:A解析: 函数y=ln,∴x≠0,故函数的定义域为{x|x≠0}.再根据y=f(x)的解析式可得f(-x)=ln=ln=f(x),故函数f(x)为偶函数,函数的图象关于y轴对称,排除B,D.当x∈(0,1)时, 00,排除B;又 x→+∞时,→0,∴排除D,故选C.5.下列函数f(x)的图象中,满足f>f(3)>f(2)的只可能是()ABCD答案:D解析:因为f>f(3)>f(2),所以函数f(x)有增有减,排除A,B.在C中,f<f(0)=1,f(3)>f(0),即f<f(3),排除C,故选D.6.[2017·河南洛阳统考]若函数y=f(2x+1)是偶函数,则函数y=f(2x)的图象的对称轴方程是()A.x=-1B.x=-C.x=D.x=1答案:C解析: f(2x+1)是偶函数,其图象关于y轴,即关于x=0对称,而f(2x+1)=f,∴f(2x)的图象可由f(2x+1)的图象向右平移个单位得到,即f(2x)的图象的对称轴方程是x=.7.设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式<0的解集为()A.(-1,0)∪(1,+∞)B.(-∞,-1)∪(0,1)C.(-∞,-1)∪(1,+∞)D.(-1,0)∪(0,1)答案:D解析:因为f(x)为奇函数,所以不等式<0可化为<0,即xf(x)<0,f(x)的大致图象如图所示.所以xf(x)<0的解集为(-1,0)∪(0,1).8.已知函数f(x)的定义域为R,且f(x)=若方程f(x)=x+a有两个不同实根,则a的取值范围为()A.(-∞,1)B.(-∞,1]C.(0,1)D.(-∞,+∞)答案:A解析:当x≤0时,f(x)=2-x-1,当00时,f(x)是周期函数,如图所示.若方程f(x)=x+a有两个不同的实数根,则函数f(x)的图象与直线y=x+a有两个不同交点,故a<1,即a的取值范围是(-∞,1).9.函数f(x)=的图象的对称中心为________.答案:(0,1)解析:因为f(x)==1+,故f(x)的对称中心为(0,1).10.若函数y=f(x+3)的图象经过点P(1,4),则函数y=f(x)的图象必经过点________.答案:(4,4)解析:函数y=f(x)的图象是由y=f(x+3)的图象向右平移3个单位长度而得到的.故y=f(x)的图象必经过点(4,4).11.设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时,f(x)的图象如图,则不等式f(x)<0的解集是________.答案:(-2,0)∪(2,5][冲刺名校能力提升练]1.已知函数f(x)=则对任意x1,x2∈R,若0<|x1|<|x2|,下列不等式成立的是()A.f(x1)+f(x2)<0B.f(x1)+f(x2)>0C.f(x1)-f(x2)>0D.f(x1)-f(x2)<0答案:D解析:函数f(x)的图象如图所示.且f(-x)=f(x),从而函数f(x)是偶函数且在[0,+∞)上是增函数.又0<|x1|<|x2|,∴f(x2)>f(x1),即f(x1)-f(x2)<0.2.[2017·浙江杭州模拟]已知函数f(x)的图象如图所示,则f(x)的解析式可能是()A.f(x)=x2-2ln|x|B.f(x)=x2-ln|x|C.f(x)=|x|-2ln|x|D.f(x)=|x|-ln|x|答案:B解析:由函数图象可得,函数f(x)为偶函数,且x>0时,函数f(x)的单调性为先减后增,最小值为正,极小值点小于1,分别对选项中各个函数求导,并求其导函数等于0的正根,可分别得1,,2,1,由此可得仅函数f(x)=x2-ln|x|符合条件.3.对于函数f(x)=lg(|x-2|+1),给出如下三个命题:①f(x+2)是偶函数;②f(x)在区间(-∞,2)上是减函数,在区间(2,+∞)上是增函数;③f(x)没有最小值.其中正确命题的个数为()A.1B.2C.3D.0答案:B解析:因为函数f(x)=lg(|x-...