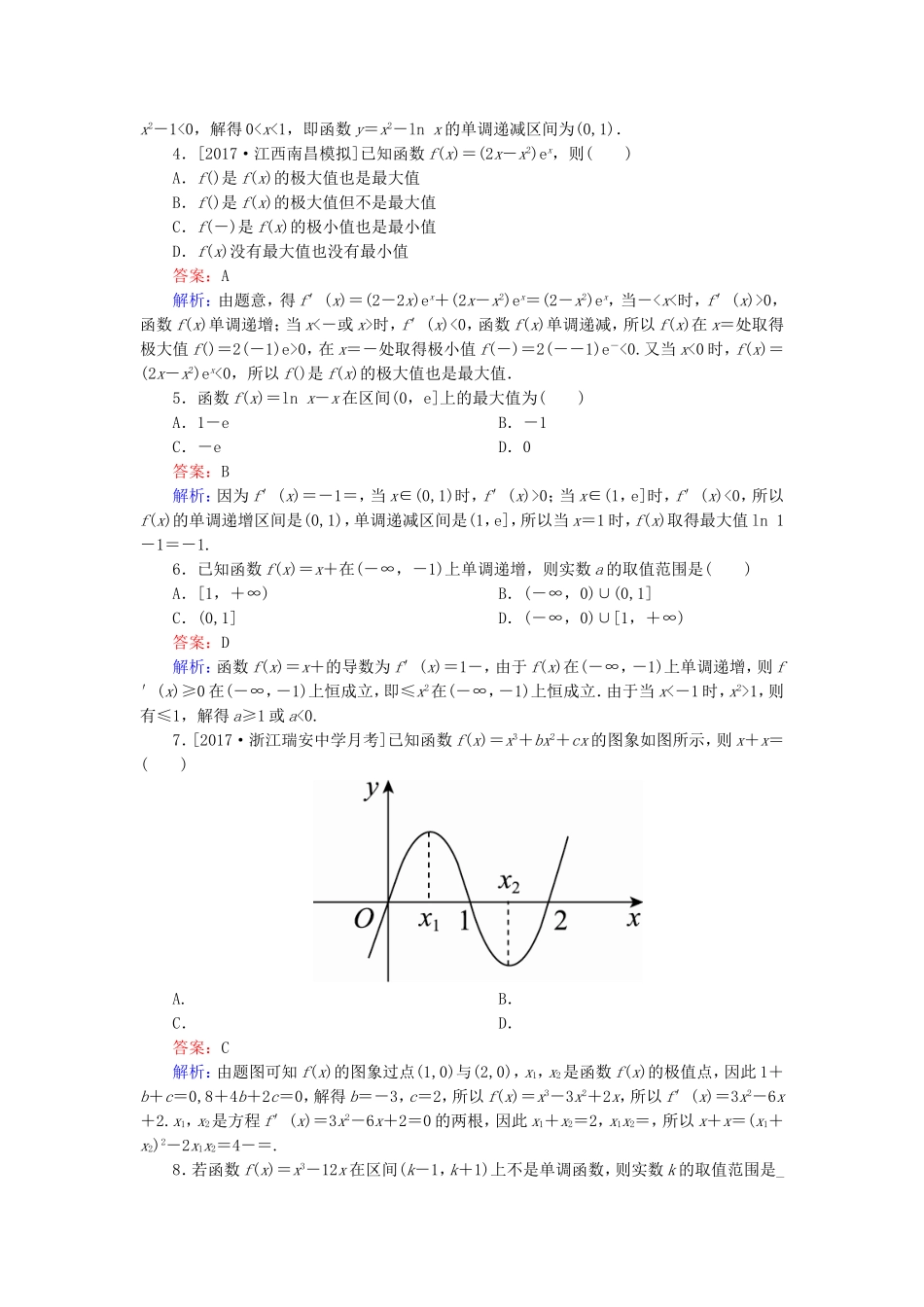
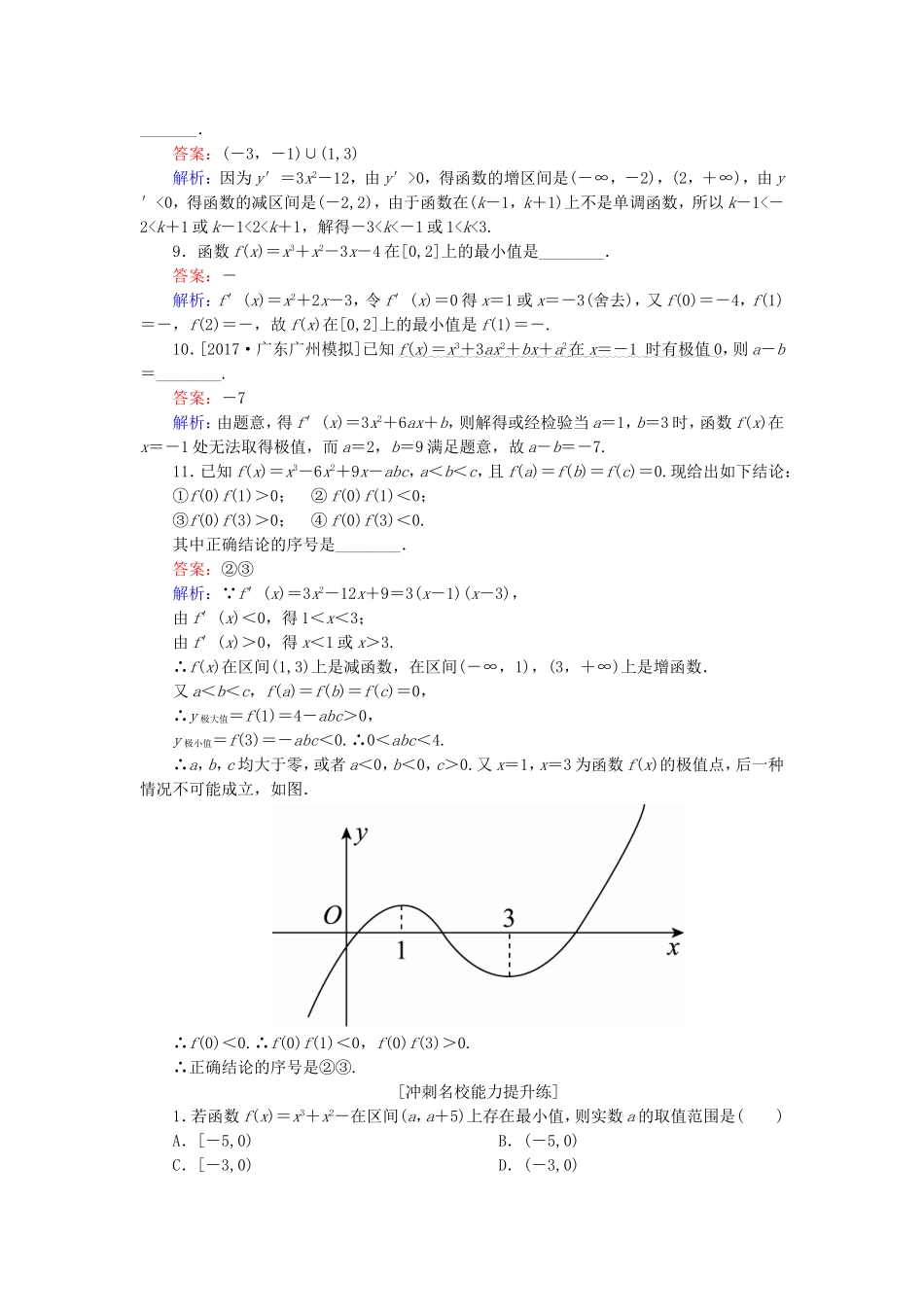
课时跟踪检测(十四)[高考基础题型得分练]1.[2017·湖南岳阳一模]下列函数中,既是奇函数又存在极值的是()A.y=x3B.y=ln(-x)C.y=xe-xD.y=x+答案:D解析:由题意知,B,C选项中的函数不是奇函数,A选项中,函数y=x3单调递增(无极值),而D选项中的函数既为奇函数又存在极值.2.已知函数f(x)的导函数f′(x)=ax2+bx+c的图象如图所示,则f(x)的图象可能是()ABCD答案:D解析:当x<0时,由导函数f′(x)=ax2+bx+c<0,知相应的函数f(x)在该区间内单调递减;当x>0时,由导函数f′(x)=ax2+bx+c的图象可知,导函数在区间(0,x1)上的值是大于0的,则在此区间内函数f(x)单调递增.3.函数y=x2-lnx的单调递减区间为()A.(0,1)B.(0,+∞)C.(1,+∞)D.(0,2)答案:A解析:对于函数y=x2-lnx,易得其定义域为{x|x>0},y′=x-=,令<0,又x>0,所以x2-1<0,解得00,函数f(x)单调递增;当x<-或x>时,f′(x)<0,函数f(x)单调递减,所以f(x)在x=处取得极大值f()=2(-1)e>0,在x=-处取得极小值f(-)=2(--1)e-<0.又当x<0时,f(x)=(2x-x2)ex<0,所以f()是f(x)的极大值也是最大值.5.函数f(x)=lnx-x在区间(0,e]上的最大值为()A.1-eB.-1C.-eD.0答案:B解析:因为f′(x)=-1=,当x∈(0,1)时,f′(x)>0;当x∈(1,e]时,f′(x)<0,所以f(x)的单调递增区间是(0,1),单调递减区间是(1,e],所以当x=1时,f(x)取得最大值ln1-1=-1.6.已知函数f(x)=x+在(-∞,-1)上单调递增,则实数a的取值范围是()A.[1,+∞)B.(-∞,0)∪(0,1]C.(0,1]D.(-∞,0)∪[1,+∞)答案:D解析:函数f(x)=x+的导数为f′(x)=1-,由于f(x)在(-∞,-1)上单调递增,则f′(x)≥0在(-∞,-1)上恒成立,即≤x2在(-∞,-1)上恒成立.由于当x<-1时,x2>1,则有≤1,解得a≥1或a<0.7.[2017·浙江瑞安中学月考]已知函数f(x)=x3+bx2+cx的图象如图所示,则x+x=()A.B.C.D.答案:C解析:由题图可知f(x)的图象过点(1,0)与(2,0),x1,x2是函数f(x)的极值点,因此1+b+c=0,8+4b+2c=0,解得b=-3,c=2,所以f(x)=x3-3x2+2x,所以f′(x)=3x2-6x+2.x1,x2是方程f′(x)=3x2-6x+2=0的两根,因此x1+x2=2,x1x2=,所以x+x=(x1+x2)2-2x1x2=4-=.8.若函数f(x)=x3-12x在区间(k-1,k+1)上不是单调函数,则实数k的取值范围是________.答案:(-3,-1)∪(1,3)解析:因为y′=3x2-12,由y′>0,得函数的增区间是(-∞,-2),(2,+∞),由y′<0,得函数的减区间是(-2,2),由于函数在(k-1,k+1)上不是单调函数,所以k-1<-2