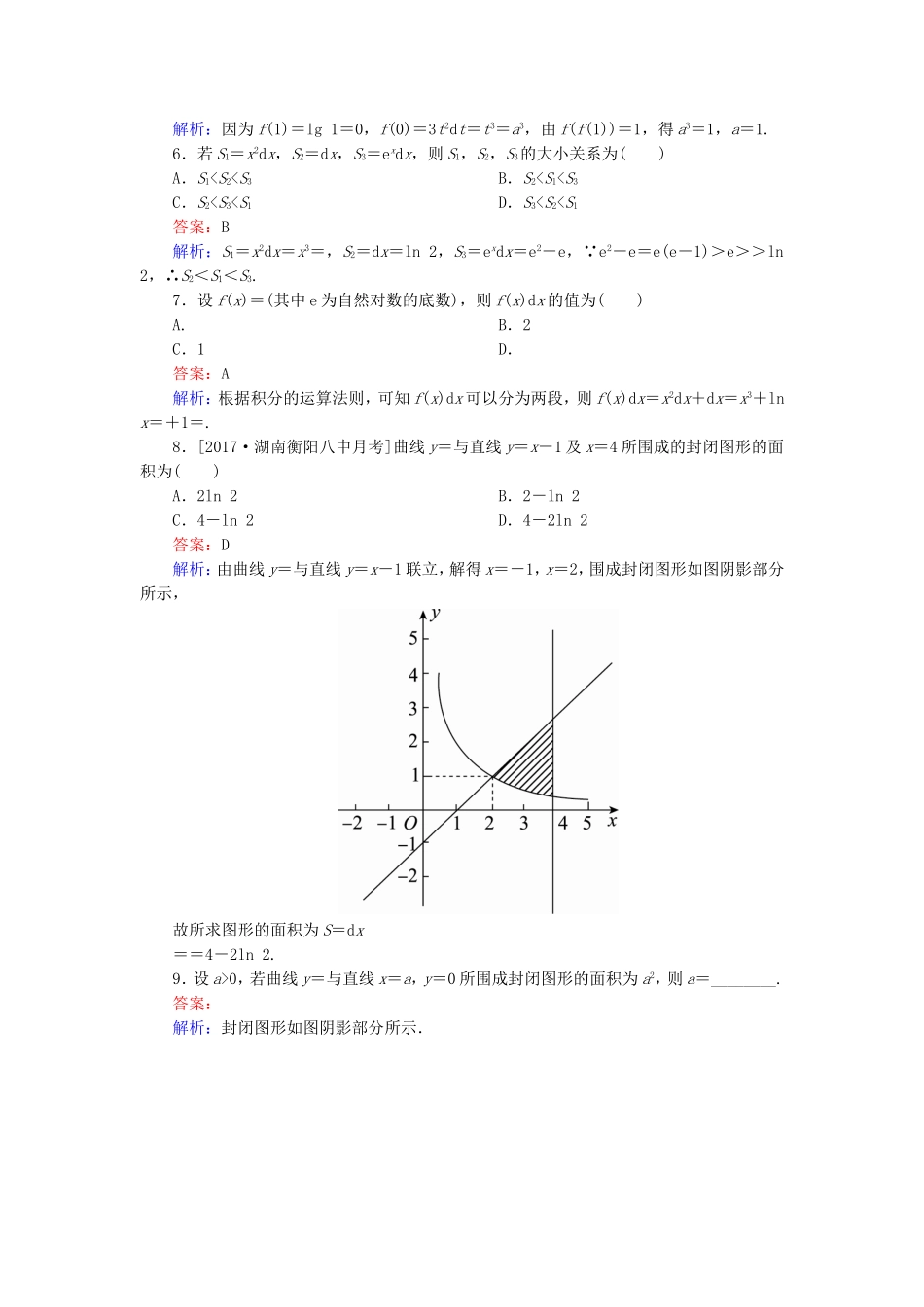
课时跟踪检测(十六)[高考基础题型得分练]1.[2017·陕西西安调研]定积分(2x+ex)dx的值为()A.e+2B.e+1C.eD.e-1答案:C解析:(2x+ex)dx=(x2+ex)=1+e1-1=e.故选C.2.直线y=4x与曲线y=x3在第一象限内围成的封闭图形的面积为()A.2B.4C.2D.4答案:D解析:如图,y=4x与y=x3的交点A(2,8),图中阴影部分即为所求图形面积.S阴=(4x-x3)dx==8-×24=4,故选D.3.从空中自由下落的一物体,在第一秒末恰经过电视塔顶,在第二秒末物体落地,已知自由落体的运动速度为v=gt(g为常数),则电视塔高为()A.gB.gC.gD.2g答案:C解析:电视塔高h=gtdt==g.4.已知f(x)=若f(x)dx=,则k的值为()A.0B.0或-1C.0或1D.-1答案:B解析: f(x)dx=(1+x2)dx=<,∴当k≥2时,f(x)dx<,∴k<2,∴f(x)dx=(2x+1)dx+(x2+1)dx=,化简得k2+k=0,解得k=0或k=-1.5.若f(x)=f(f(1))=1,则a的值为()A.1B.2C.-1D.-2答案:A解析:因为f(1)=lg1=0,f(0)=3t2dt=t3=a3,由f(f(1))=1,得a3=1,a=1.6.若S1=x2dx,S2=dx,S3=exdx,则S1,S2,S3的大小关系为()A.S10,若曲线y=与直线x=a,y=0所围成封闭图形的面积为a2,则a=________.答案:解析:封闭图形如图阴影部分所示.则dx=x=a-0=a2,解得a=.10.汽车以v=3t+2(单位:m/s)作变速直线运动时,在第1s至第2s间的1s内经过的路程是________m.答案:6.5解析:由题意,得s=(3t+2)dt==×4+4-=10-=(m).11.函数f(x)=的图象与直线x=1及x轴所围成的封闭图形的面积为________.答案:e-解析:由题意知,所求面积为-1(x+1)dx+exdx=+ex=-+(e-1)=e-.12.如图所示,由抛物线y=-x2+4x-3及其在点A(0,-3)和点B(3,0)处的切线所围成的图形的面积为________.答案:解析:由题意,知抛物线y=-x2+4x-3在点A处的切线斜率是k1=y′|x=0=4,在点B处的切线斜率是k2=y′|x=3=-2.因此,抛物线过点A的切线方程为y=4x-3,过点B的切线方程为y=-2x+6.设两切线相交于点M,由消去y,得x=,即点M的横坐标为.在区间上,直线y=4x-3在曲线y=-x2+4x-3的上方;在区间上,直线y=-2x+6在曲线y=-x2+4x-3的上方.因此,所求的图形的面积是S=[(4x-3)-(-x2+4x-3)]dx+[(-2x+6)-(-x2+4x-3)]dx=x2dx+(x2-6x+9)dx=+=.[冲刺名校能力提升练]1.若f(x)=x2+2f(x)dx,则f(x)dx=()A.-1B.-C.D.1答案:B解析:由题意知f(x)=x2+2f(x)dx,设m=f(x)dx,∴f(x)=x2+2m,f(x)dx=(x2+2m)dx==+2m=m,∴m=-.2.已知函数f(x)=sin(x-φ),且f(x)dx=0,则函数f(x)的图象的一条对称轴是()A.x=B.x=C.x=D.x=答案:A解析:由f(x)dx=0,得sin(x-φ)dx=0,即-cos(x-φ)=0,∴-cos+cosφ=0,∴cosφ-sinφ=0,∴cos=0,∴φ+=+kπ(k∈Z),解得φ=kπ+(k∈Z),∴f(x)=sin,由x-kπ-=k′π+,得x=(k+k′)π+(k,k′∈Z),故选A.3.若函数f(x),g(x)满足f(x)g(x)dx=0,则称f(x),g(x)为区间[-1,1]上的一组正交函数.给出三组函数:①f(x)=sinx,g(x)=cosx;②f(x)=x+1,g(x)=x-1;③f(x)=x,g(x)=x2.其中为区间[-1,1]上的正交函数的组数是________.(填序号)答案:①③解析:①中f(x)g(x)dx=dx=dx=0;②中f(x)g(x)dx=-1(x+1)(x-1)dx=(x2-1)dx==-≠0;③中f(x)·g(x)=x3为奇函数,在[-1,1]上的积分为0,故①③满足条件...