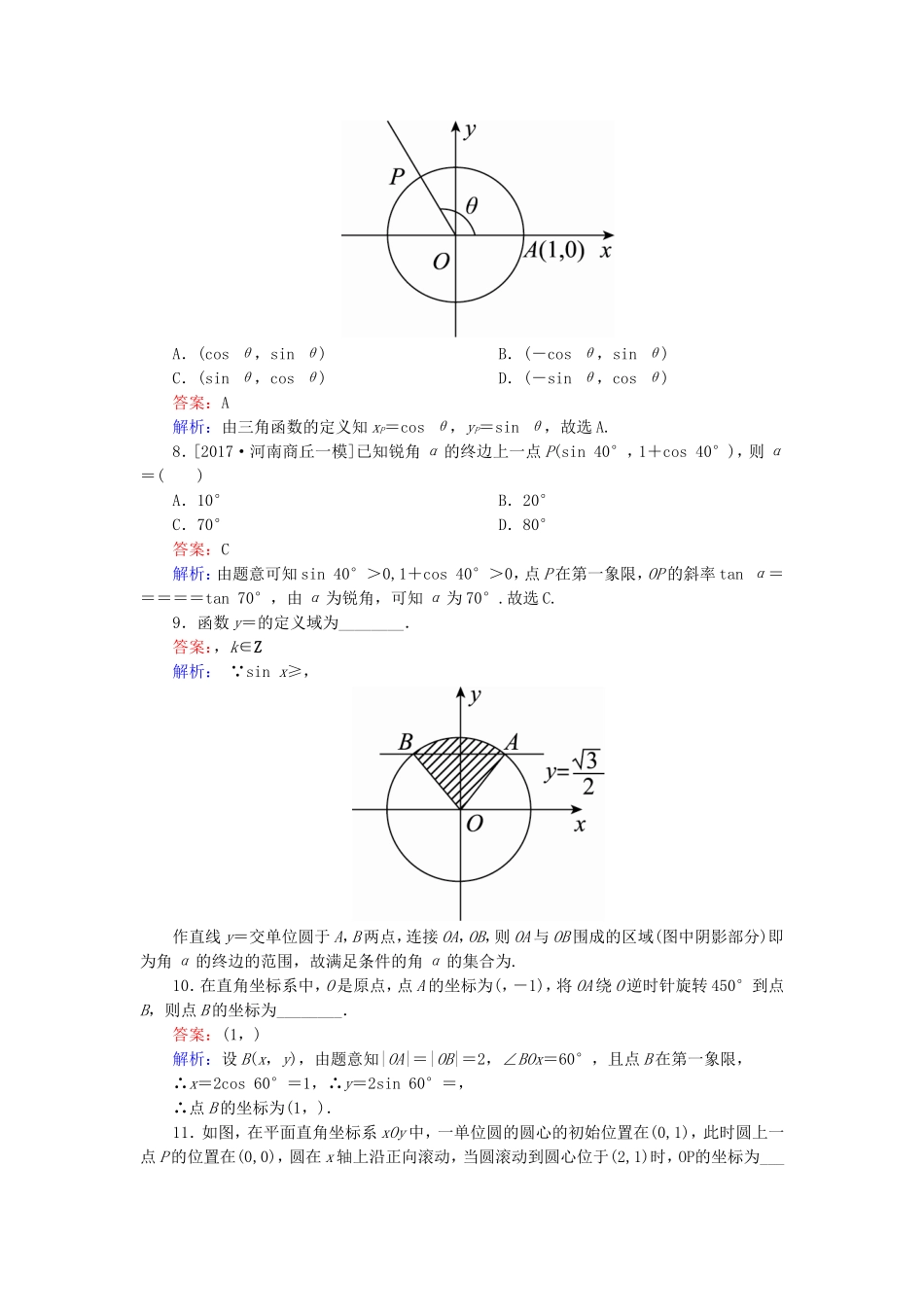
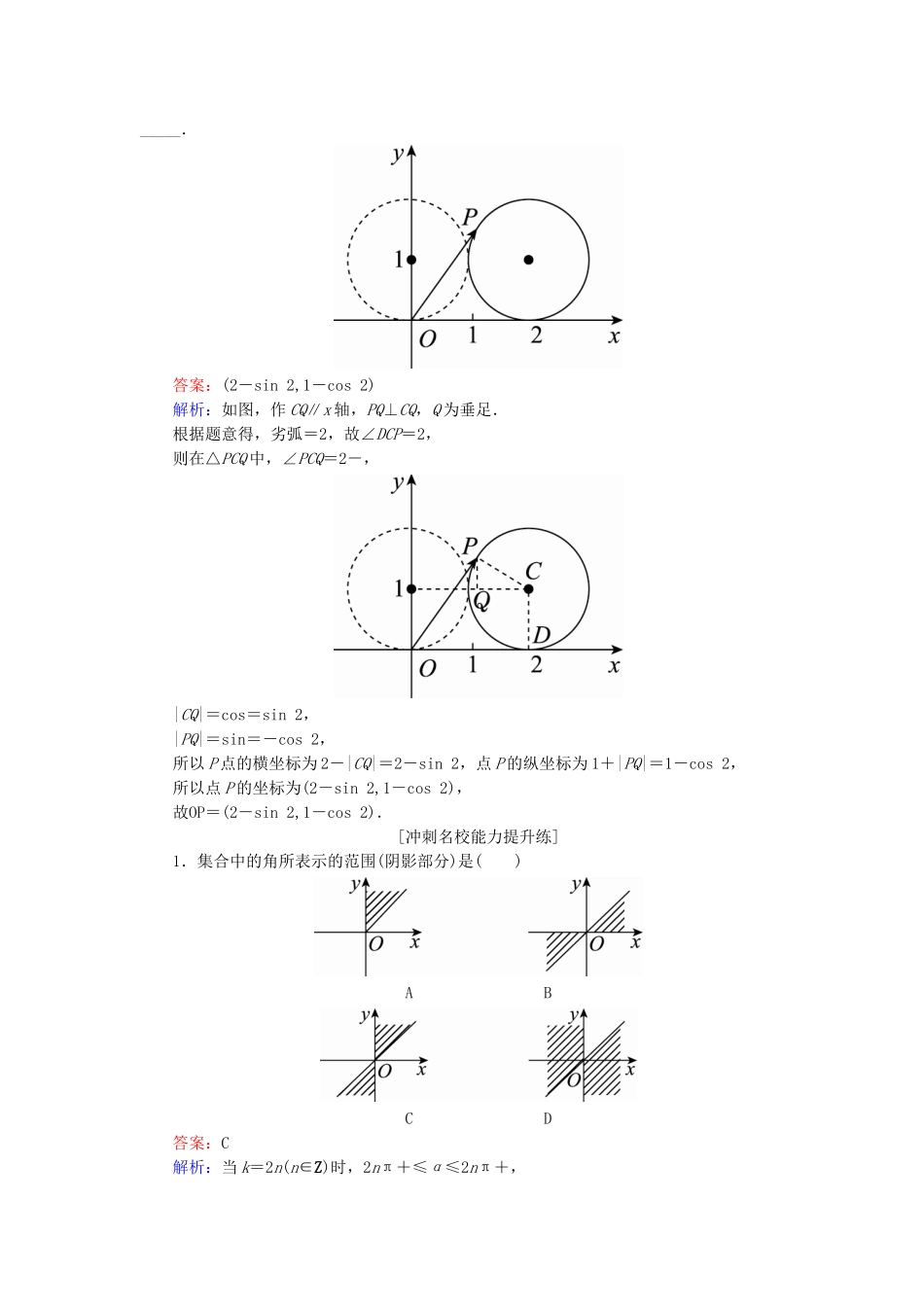
课时跟踪检测(十八)[高考基础题型得分练]1.下列与的终边相同的角的表达式中正确的是()A.2kπ+45°(k∈Z)B.k·360°+(k∈Z)C.k·360°-315°(k∈Z)D.kπ+(k∈Z)答案:C解析:与的终边相同的角可以写成2kπ+(k∈Z),但是角度制与弧度制不能混用,所以只有C正确.2.已知角α的终边经过点(-4,3),则cosα=()A.B.C.-D.-答案:D解析:由三角函数的定义知,cosα==-.3.已知点P(tanα,cosα)在第三象限,则角α的终边在()A.第一象限B.第二象限C.第三象限D.第四象限答案:B解析:由题意知tanα<0,cosα<0,∴α是第二象限角.4.若tanα>0,则()A.sin2α>0B.cosα>0C.sinα>0D.cos2α>0答案:A解析:由tanα>0可得,α的终边在第一象限或第三象限,此时sinα与cosα同号,故sin2α=2sinαcosα>0,故选A.5.已知点P落在角θ的终边上,且θ∈[0,2π),则θ的值为()A.B.C.D.答案:D解析:由sin>0,cos<0知角θ是第四象限的角,∵tanθ==-1,θ∈[0,2π),∴θ=.6.若α是第三象限角,则y=+的值为()A.0B.2C.-2D.2或-2答案:A解析:∵α是第三象限角,∴2kπ+π<α<2kπ+(k∈Z),∴kπ+<<kπ+(k∈Z),∴是第二象限角或第四象限角.当是第二象限角时,y=-=0;当是第四象限角时,y=-+=0.故选A.7.[2017·浙江杭州模拟]如图所示,在直角坐标系xOy中,射线OP交单位圆O于点P,若∠AOP=θ,则点P的坐标是()A.(cosθ,sinθ)B.(-cosθ,sinθ)C.(sinθ,cosθ)D.(-sinθ,cosθ)答案:A解析:由三角函数的定义知xP=cosθ,yP=sinθ,故选A.8.[2017·河南商丘一模]已知锐角α的终边上一点P(sin40°,1+cos40°),则α=()A.10°B.20°C.70°D.80°答案:C解析:由题意可知sin40°>0,1+cos40°>0,点P在第一象限,OP的斜率tanα=====tan70°,由α为锐角,可知α为70°.故选C.9.函数y=的定义域为________.答案:,k∈Z解析:∵sinx≥,作直线y=交单位圆于A,B两点,连接OA,OB,则OA与OB围成的区域(图中阴影部分)即为角α的终边的范围,故满足条件的角α的集合为.10.在直角坐标系中,O是原点,点A的坐标为(,-1),将OA绕O逆时针旋转450°到点B,则点B的坐标为________.答案:(1,)解析:设B(x,y),由题意知|OA|=|OB|=2,∠BOx=60°,且点B在第一象限,∴x=2cos60°=1,∴y=2sin60°=,∴点B的坐标为(1,).11.如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动,当圆滚动到圆心位于(2,1)时,OP的坐标为________.答案:(2-sin2,1-cos2)解析:如图,作CQ∥x轴,PQ⊥CQ,Q为垂足.根据题意得,劣弧=2,故∠DCP=2,则在△PCQ中,∠PCQ=2-,|CQ|=cos=sin2,|PQ|=sin=-cos2,所以P点的横坐标为2-|CQ|=2-sin2,点P的纵坐标为1+|PQ|=1-cos2,所以点P的坐标为(2-sin2,1-cos2),故OP=(2-sin2,1-cos2).[冲刺名校能力提升练]1.集合中的角所表示的范围(阴影部分)是()ABCD答案:C解析:当k=2n(n∈Z)时,2nπ+≤α≤2nπ+,此时α表示的范围与≤α≤表示的范围一样;当k=2n+1(n∈Z)时,2nπ+π+≤α≤2nπ+π+,此时α表示的范围与π+≤α≤π+表示的范围一样.2.[2017·江西南昌二中模拟]已知角α终边上一点P的坐标是(2sin2,-2cos2),则sinα=()A.sin2B.-sin2C.cos2D.-cos2答案:D解析:因为r==2,由任意三角函数的定义,得sinα==-cos2.3.将表的分针拨快10分钟,则分针旋转过程中形成的角的弧度数是________.答案:-解析:将表的分针拨快应按顺时针方向旋转,为负角.故A,B不正确,又因为拨快10分钟,故应转过的角为圆周的,即为-×2π=-.4.已知一扇形的圆心角为α(α>0),所在圆的半径为R.(1)若α=60°,R=10cm,求扇形的弧长及该弧所在的弓形的面积;(2)若扇形的周长是一定值C(C>0),当α为多少弧度时,该扇形有最大面积?解:(1)设弧长为l,弓形面积为S弓,则α=60°=,R=10,l=×10=(cm),S弓=S扇-S△=××10-×102×sin=π-=50(cm2).(2)扇形周长C=2R+l=2R+αR,∴R=,∴S扇=α·R2=α·2=·=·≤.当且仅当α2=4,即α=2时,扇形面积有最大值.