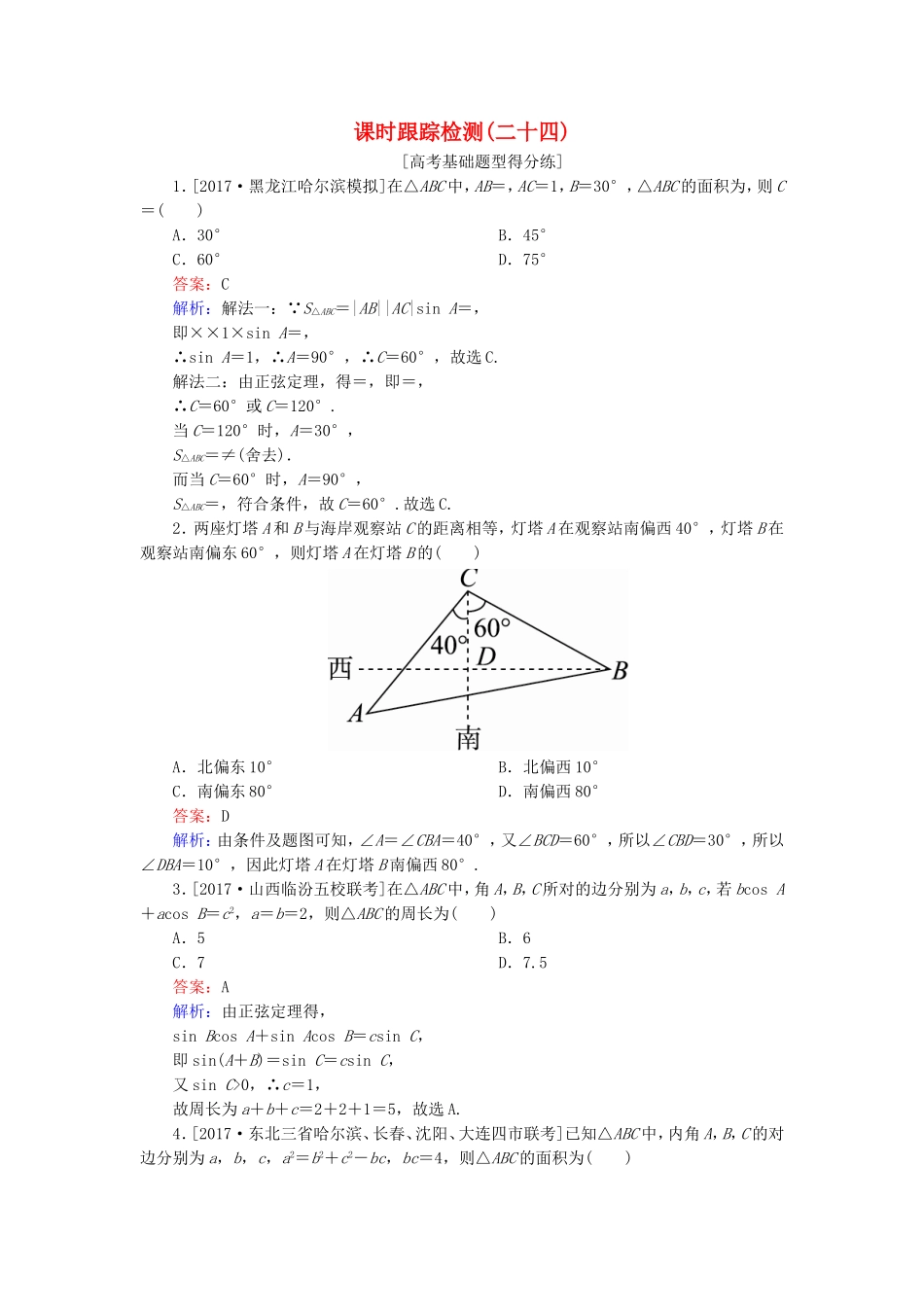
课时跟踪检测(二十四)[高考基础题型得分练]1.[2017·黑龙江哈尔滨模拟]在△ABC中,AB=,AC=1,B=30°,△ABC的面积为,则C=()A.30°B.45°C.60°D.75°答案:C解析:解法一: S△ABC=|AB||AC|sinA=,即××1×sinA=,∴sinA=1,∴A=90°,∴C=60°,故选C.解法二:由正弦定理,得=,即=,∴C=60°或C=120°.当C=120°时,A=30°,S△ABC=≠(舍去).而当C=60°时,A=90°,S△ABC=,符合条件,故C=60°.故选C.2.两座灯塔A和B与海岸观察站C的距离相等,灯塔A在观察站南偏西40°,灯塔B在观察站南偏东60°,则灯塔A在灯塔B的()A.北偏东10°B.北偏西10°C.南偏东80°D.南偏西80°答案:D解析:由条件及题图可知,∠A=∠CBA=40°,又∠BCD=60°,所以∠CBD=30°,所以∠DBA=10°,因此灯塔A在灯塔B南偏西80°.3.[2017·山西临汾五校联考]在△ABC中,角A,B,C所对的边分别为a,b,c,若bcosA+acosB=c2,a=b=2,则△ABC的周长为()A.5B.6C.7D.7.5答案:A解析:由正弦定理得,sinBcosA+sinAcosB=csinC,即sin(A+B)=sinC=csinC,又sinC>0,∴c=1,故周长为a+b+c=2+2+1=5,故选A.4.[2017·东北三省哈尔滨、长春、沈阳、大连四市联考]已知△ABC中,内角A,B,C的对边分别为a,b,c,a2=b2+c2-bc,bc=4,则△ABC的面积为()A.B.1C.D.2答案:C解析: a2=b2+c2-bc,∴cosA=,∴A=,又bc=4,∴△ABC的面积为bcsinA=,故选C.5.在200米高的山顶上,测得山下一塔顶与塔底的俯角分别为30°,60°,则塔高是()A.米B.米C.200米D.200米答案:A解析:如图所示,AB为山高,CD为塔高,则由题意知,在Rt△ABC中,∠BAC=30°,AB=200(米).则AC==(米).在△ACD中,∠CAD=60°-30°=30°,∠ACD=30°,∴∠ADC=120°.由正弦定理得=,∴CD==(米).6.在△ABC中,已知b=40,c=20,C=60°,则此三角形的解的情况是()A.有一解B.有两解C.无解D.有解但解的个数不确定答案:C解析:由正弦定理,得=,∴sinB===>1.∴角B不存在,即满足条件的三角形不存在.7.[2017·东北三省三校联考]△ABC的内角A,B,C的对边分别为a,b,c,则“a>b”是“cos2A<cos2B”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案:C解析:因为在△ABC中,a>b⇔sinA>sinB⇔sin2A>sin2B⇔2sin2A>2sin2B⇔1-2sin2A<1-2sin2B⇔cos2A<cos2B.所以“a>b”是“cos2A<cos2B”的充分必要条件.8.[2017·北京海淀区模拟]在△ABC中,角A,B,C的对边分别为a,b,c.若c=4,sinC=2sinA,sinB=,则S△ABC=________.答案:解析: sinC=2sinA,由正弦定理可得c=2a, c=4,∴a=2,∴S△ABC=acsinB=×2×4×=.9.[2017·江西南昌二中模拟]在△ABC中,如果cos(B+A)+2sinAsinB=1,那么△ABC的形状是________.答案:等腰三角形解析: cos(B+A)+2sinAsinB=1,∴cosAcosB+sinAsinB=1,∴cos(A-B)=1,在△ABC中,A-B=0⇒A=B,∴△ABC是等腰三角形.10.[2017·陕西八校联考]设△ABC的三边长分别为a,b,c,面积为S,且满足S=a2-(b-c)2,b+c=8,则S的最大值为________.答案:解析: S=a2-(b-c)2,b+c=8,∴bcsinA=2bc-(b2+c2-a2)=2bc-2bccosA,即sinA+4cosA=4.联立解得sinA=,∴S=bcsinA=bc≤×2=,当且仅当b=c=4时等号成立.11.如图,为测得河岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点C到点A的仰角为60°,再由点C沿北偏东15°方向走10米到位置D,测得∠BDC=45°,则塔AB的高是________米.答案:10解析:在△BCD中,CD=10,∠BDC=45°,∠BCD=15°+90°=105°,∠DBC=30°,由正弦定理得=,所以BC==10.在Rt△ABC中,tan60°=,AB=BCtan60°=10(米).[冲刺名校能力提升练]1.已知a,b,c分别为△ABC三个内角A,B,C的对边,且(b-c)(sinB+sinC)=(a-c)sinA,则角B的大小为()A.30°B.45°C.60°D.120°答案:A解析:由正弦定理==及(b-c)·(sinB+sinC)=(a-c)sinA得(b-c)(b+c)=(a-c)a,即b2-c2=a2-ac,所...