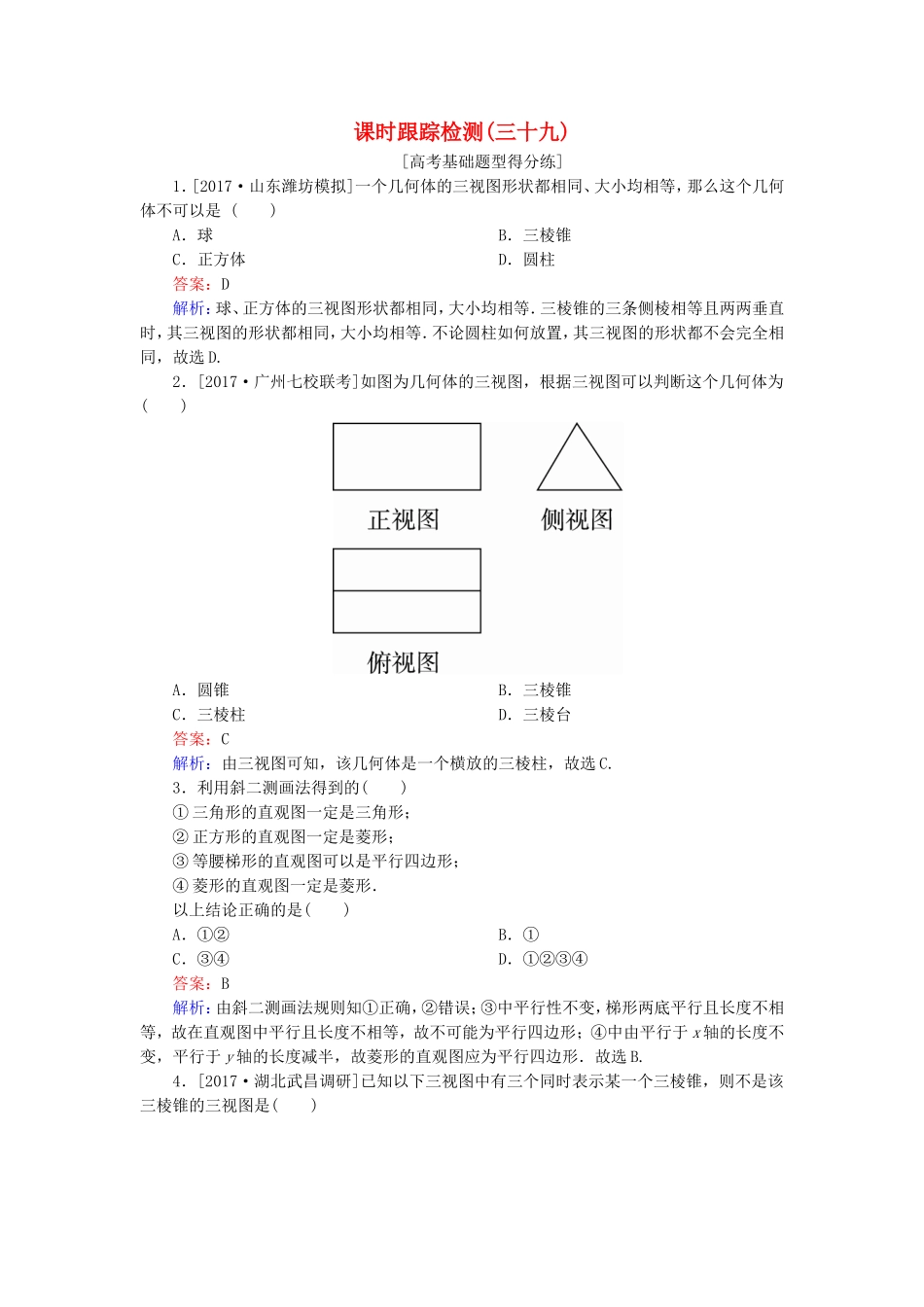
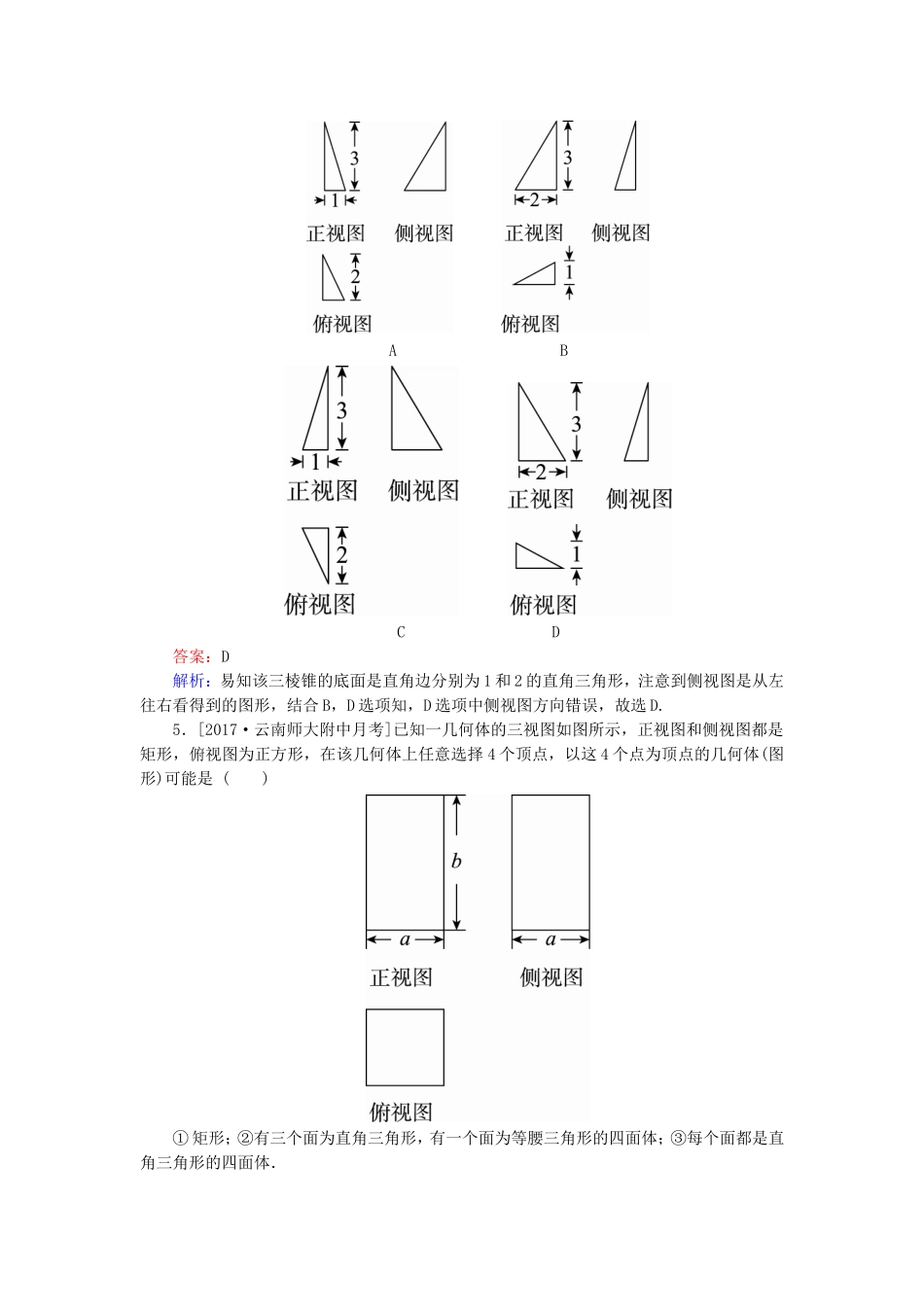
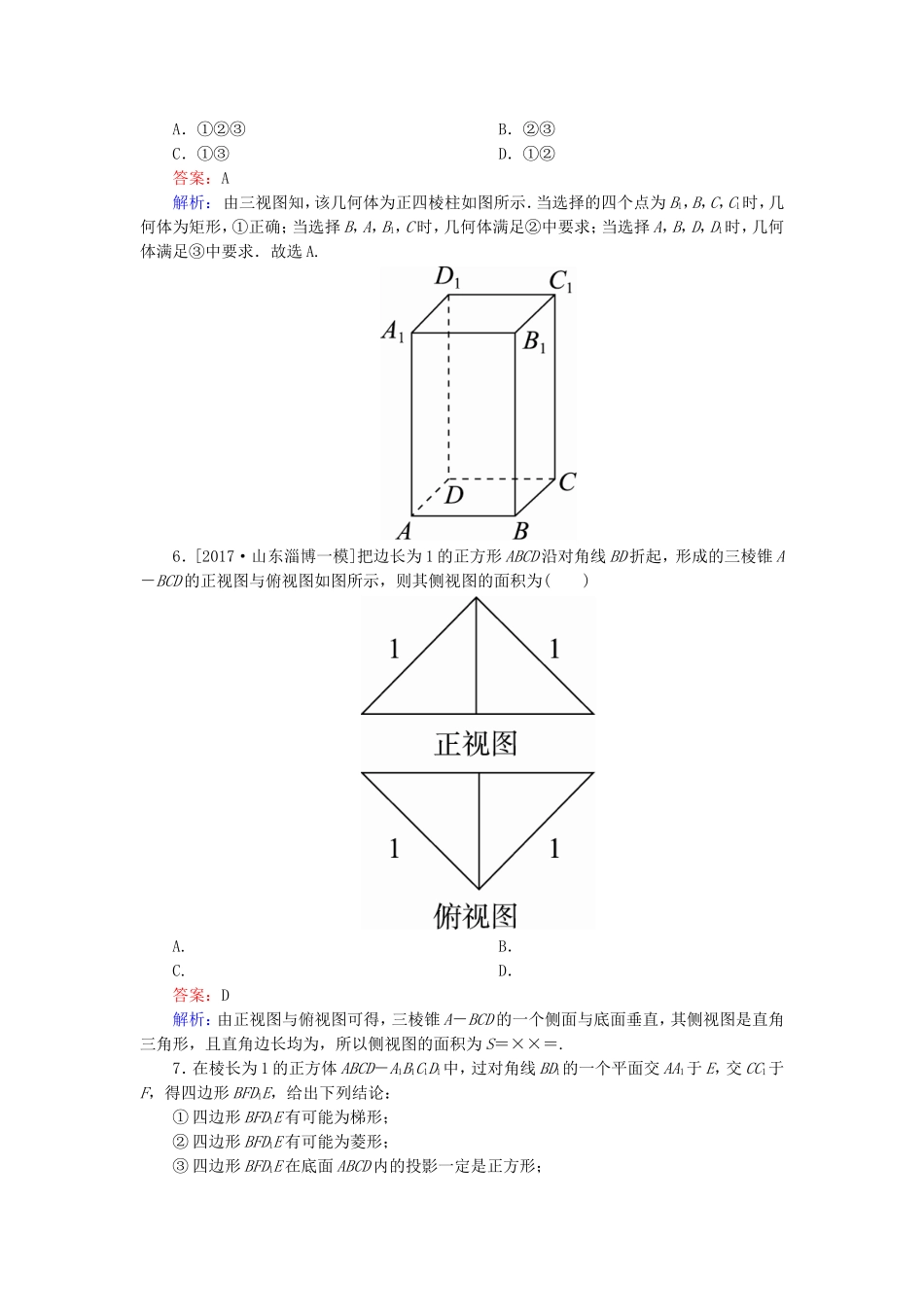
课时跟踪检测(三十九)[高考基础题型得分练]1.[2017·山东潍坊模拟]一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是()A.球B.三棱锥C.正方体D.圆柱答案:D解析:球、正方体的三视图形状都相同,大小均相等.三棱锥的三条侧棱相等且两两垂直时,其三视图的形状都相同,大小均相等.不论圆柱如何放置,其三视图的形状都不会完全相同,故选D.2.[2017·广州七校联考]如图为几何体的三视图,根据三视图可以判断这个几何体为()A.圆锥B.三棱锥C.三棱柱D.三棱台答案:C解析:由三视图可知,该几何体是一个横放的三棱柱,故选C.3.利用斜二测画法得到的()①三角形的直观图一定是三角形;②正方形的直观图一定是菱形;③等腰梯形的直观图可以是平行四边形;④菱形的直观图一定是菱形.以上结论正确的是()A.①②B.①C.③④D.①②③④答案:B解析:由斜二测画法规则知①正确,②错误;③中平行性不变,梯形两底平行且长度不相等,故在直观图中平行且长度不相等,故不可能为平行四边形;④中由平行于x轴的长度不变,平行于y轴的长度减半,故菱形的直观图应为平行四边形.故选B.4.[2017·湖北武昌调研]已知以下三视图中有三个同时表示某一个三棱锥,则不是该三棱锥的三视图是()ABCD答案:D解析:易知该三棱锥的底面是直角边分别为1和2的直角三角形,注意到侧视图是从左往右看得到的图形,结合B,D选项知,D选项中侧视图方向错误,故选D.5.[2017·云南师大附中月考]已知一几何体的三视图如图所示,正视图和侧视图都是矩形,俯视图为正方形,在该几何体上任意选择4个顶点,以这4个点为顶点的几何体(图形)可能是()①矩形;②有三个面为直角三角形,有一个面为等腰三角形的四面体;③每个面都是直角三角形的四面体.A.①②③B.②③C.①③D.①②答案:A解析:由三视图知,该几何体为正四棱柱如图所示.当选择的四个点为B1,B,C,C1时,几何体为矩形,①正确;当选择B,A,B1,C时,几何体满足②中要求;当选择A,B,D,D1时,几何体满足③中要求.故选A.6.[2017·山东淄博一模]把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为()A.B.C.D.答案:D解析:由正视图与俯视图可得,三棱锥A-BCD的一个侧面与底面垂直,其侧视图是直角三角形,且直角边长均为,所以侧视图的面积为S=××=.7.在棱长为1的正方体ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,得四边形BFD1E,给出下列结论:①四边形BFD1E有可能为梯形;②四边形BFD1E有可能为菱形;③四边形BFD1E在底面ABCD内的投影一定是正方形;④四边形BFD1E有可能垂直于平面BB1D1D;⑤四边形BFD1E面积的最小值为.其中正确的是()A.①②③④B.②③④⑤C.①③④⑤D.①②④⑤答案:B解析:四边形BFD1E为平行四边形,①显然不成立,当E,F分别为AA1,CC1的中点时,②④成立,四边形BFD1E在底面的投影恒为正方形ABCD.当E,F分别为AA1,CC1的中点时,四边形BFD1E的面积最小,最小值为.故选B.8.如图,点O为正方体ABCD-A′B′C′D′的中心,点E为平面B′BCC′的中心,点F为B′C′的中点,则空间四边形D′OEF在该正方体的各个面上的投影可能是________.(填出所有可能的序号)答案:①②③解析:空间四边形D′OEF在正方体的平面DCC′D′上的投影是①;在平面BCC′B′上的投影是②;在平面ABCD上的投影是③,而不可能出现的投影为④的情况.9.在如图所示的直观图中,四边形O′A′B′C′为菱形且边长为2cm,则在直角坐标系xOy中,四边形ABCO为________,面积为________cm2.答案:矩形8解析:由斜二测画法的特点可知,该平面图形是一个长为4cm、宽为2cm的矩形,所以面积为8cm2.[冲刺名校能力提升练]1.[2017·湖南长沙三校一模]已知点E、F、G分别是正方体ABCD-A1B1C1D1的棱AA1,CC1,DD1的中点,点M,N,Q,P分别在线段DF,AG,BE,C1B1上.以M,N,Q,P为顶点的三棱锥P-MNQ的俯视图不可能是()答案:C解析:当M与F重合、N与G重合、Q与E重合、P与B1重合时,三棱锥P-MNQ的俯视图为A;当M,N,Q,P是所在线段的中点时,三棱锥P-MNQ的俯视图为B;当...