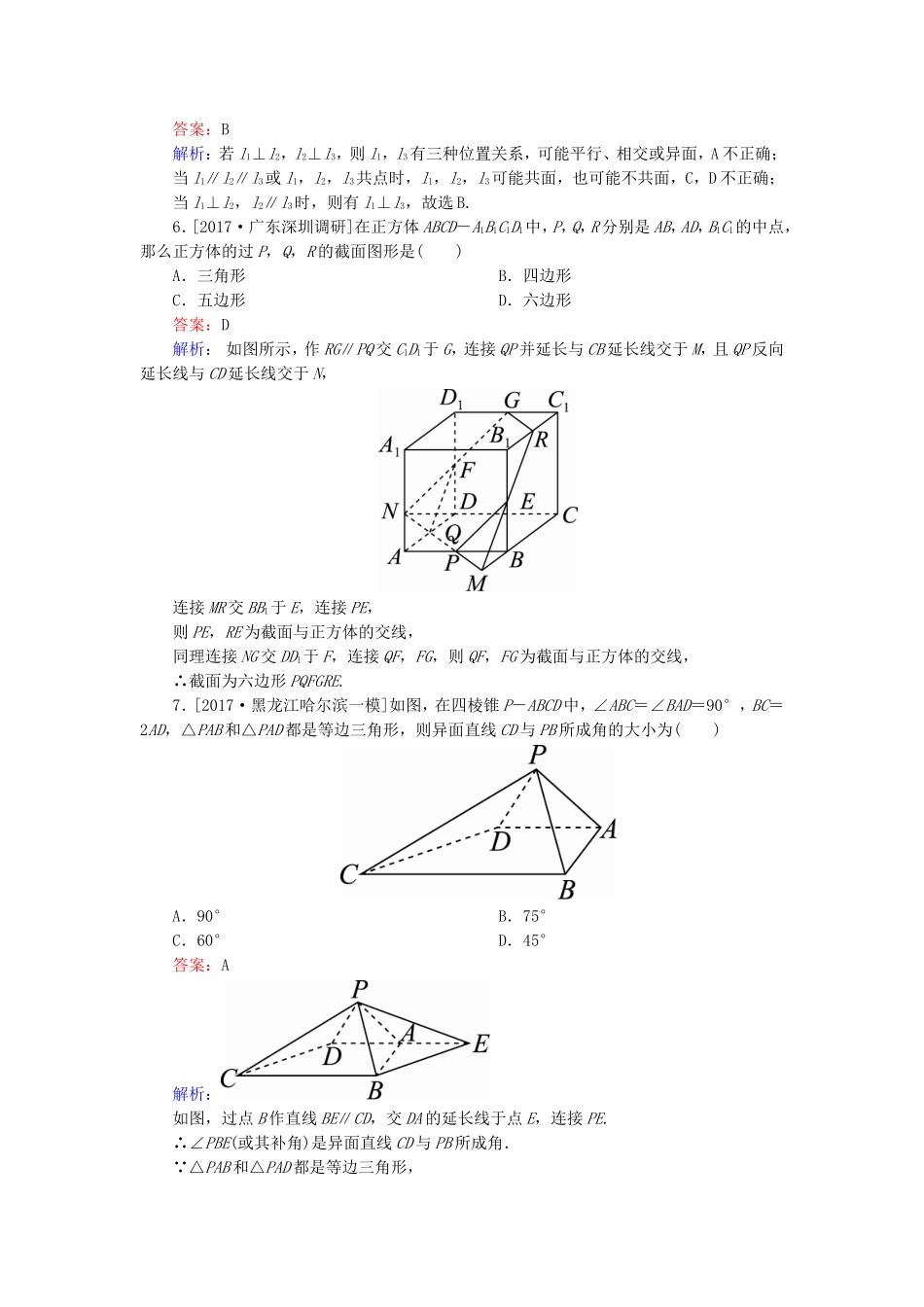
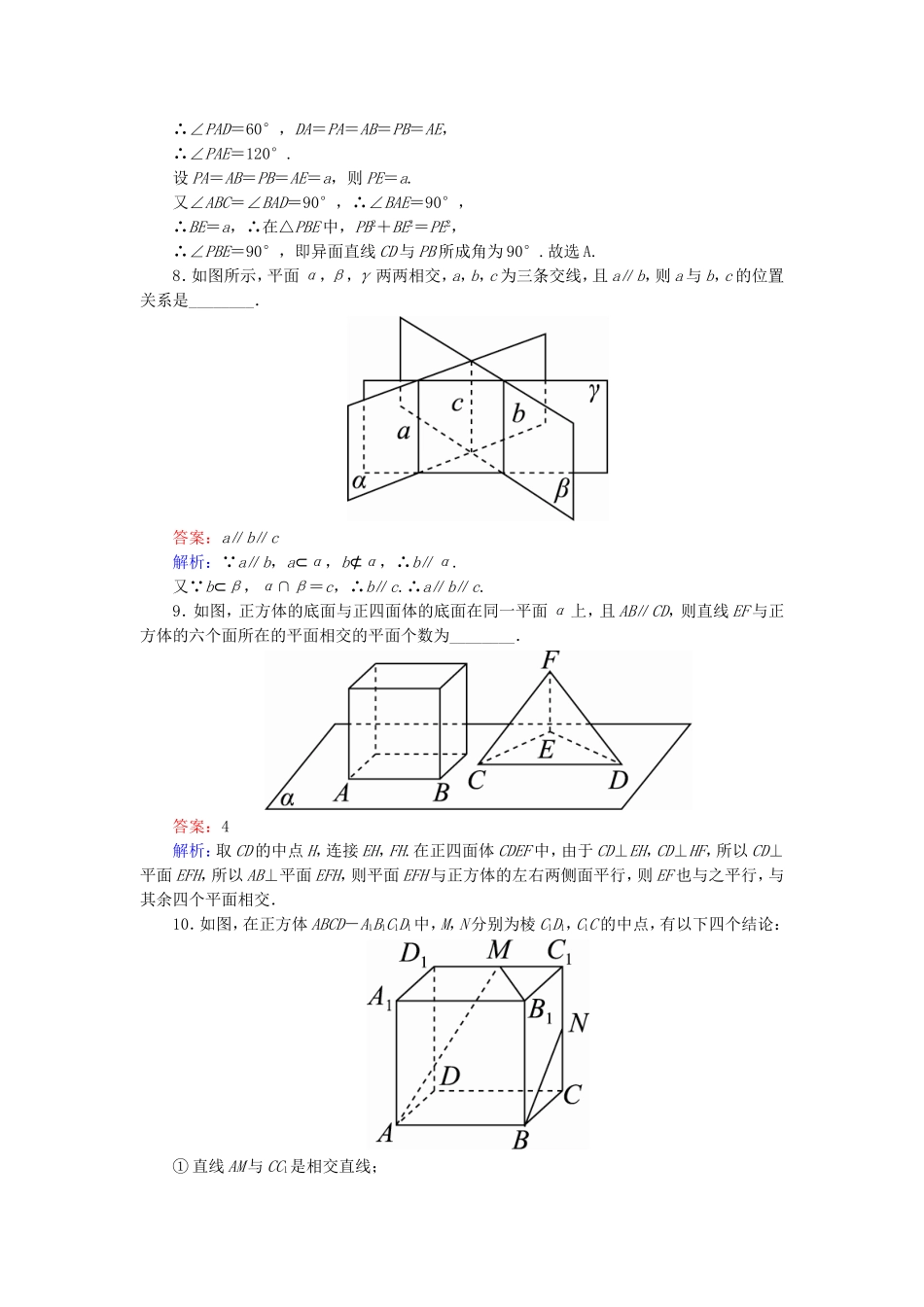
课时跟踪检测(四十一)[高考基础题型得分练]1.在下列命题中,不是公理的是()A.平行于同一个平面的两个平面相互平行B.过不在同一条直线上的三点,有且只有一个平面C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线答案:A解析:选项A是面面平行的性质定理,是由公理推证出来的.2.[2017·江西七校联考]已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面答案:D解析:依题意,直线b和c的位置关系可能是相交、平行或异面,故选D.3.在正方体ABCD-A1B1C1D1中,E,F分别是线段BC,CD1的中点,则直线A1B与直线EF的位置关系是()A.相交B.异面C.平行D.垂直答案:A解析:如图所示,直线A1B与直线外一点E确定的平面为A1BCD1,EF⊂平面A1BCD1,且两直线不平行,故两直线相交.4.若空间三条直线a,b,c满足a⊥b,b⊥c,则直线a与c()A.一定平行B.一定相交C.一定是异面直线D.平行、相交或异面都有可能答案:D解析:当a,b,c共面时,a∥c;当a,b,c不共面时,a与c可能异面也可能相交.5.l1,l2,l3是空间三条不同的直线,则下列命题正确的是()A.l1⊥l2,l2⊥l3⇒l1∥l3B.l1⊥l2,l2∥l3⇒l1⊥l3C.l1∥l2∥l3⇒l1,l2,l3共面D.l1,l2,l3共点⇒l1,l2,l3共面答案:B解析:若l1⊥l2,l2⊥l3,则l1,l3有三种位置关系,可能平行、相交或异面,A不正确;当l1∥l2∥l3或l1,l2,l3共点时,l1,l2,l3可能共面,也可能不共面,C,D不正确;当l1⊥l2,l2∥l3时,则有l1⊥l3,故选B.6.[2017·广东深圳调研]在正方体ABCD-A1B1C1D1中,P,Q,R分别是AB,AD,B1C1的中点,那么正方体的过P,Q,R的截面图形是()A.三角形B.四边形C.五边形D.六边形答案:D解析:如图所示,作RG∥PQ交C1D1于G,连接QP并延长与CB延长线交于M,且QP反向延长线与CD延长线交于N,连接MR交BB1于E,连接PE,则PE,RE为截面与正方体的交线,同理连接NG交DD1于F,连接QF,FG,则QF,FG为截面与正方体的交线,∴截面为六边形PQFGRE.7.[2017·黑龙江哈尔滨一模]如图,在四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等边三角形,则异面直线CD与PB所成角的大小为()A.90°B.75°C.60°D.45°答案:A解析:如图,过点B作直线BE∥CD,交DA的延长线于点E,连接PE.∴∠PBE(或其补角)是异面直线CD与PB所成角. △PAB和△PAD都是等边三角形,∴∠PAD=60°,DA=PA=AB=PB=AE,∴∠PAE=120°.设PA=AB=PB=AE=a,则PE=a.又∠ABC=∠BAD=90°,∴∠BAE=90°,∴BE=a,∴在△PBE中,PB2+BE2=PE2,∴∠PBE=90°,即异面直线CD与PB所成角为90°.故选A.8.如图所示,平面α,β,γ两两相交,a,b,c为三条交线,且a∥b,则a与b,c的位置关系是________.答案:a∥b∥c解析: a∥b,a⊂α,b⊄α,∴b∥α.又 b⊂β,α∩β=c,∴b∥c.∴a∥b∥c.9.如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为________.答案:4解析:取CD的中点H,连接EH,FH.在正四面体CDEF中,由于CD⊥EH,CD⊥HF,所以CD⊥平面EFH,所以AB⊥平面EFH,则平面EFH与正方体的左右两侧面平行,则EF也与之平行,与其余四个平面相交.10.如图,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,有以下四个结论:①直线AM与CC1是相交直线;②直线AM与BN是平行直线;③直线BN与MB1是异面直线;④直线AM与DD1是异面直线.其中正确的结论为________.(写出全部正确结论的序号)答案:③④解析:A,M,C1三点共面,且在平面AD1C1B中,C∉平面AD1C1B,C1∉AM,因此直线AM与CC1是异面直线.同理AM与BN也是异面直线,AM与DD1也是异面直线,①②错误,④正确;M,B,B1三点共面,且在平面MBB1中,N∉平面MBB1,B∉MB1,因此直线BN与MB1是异面直线,③正确.11.设a,b,c是空间中的三条直线,下面给出五个命题:①...