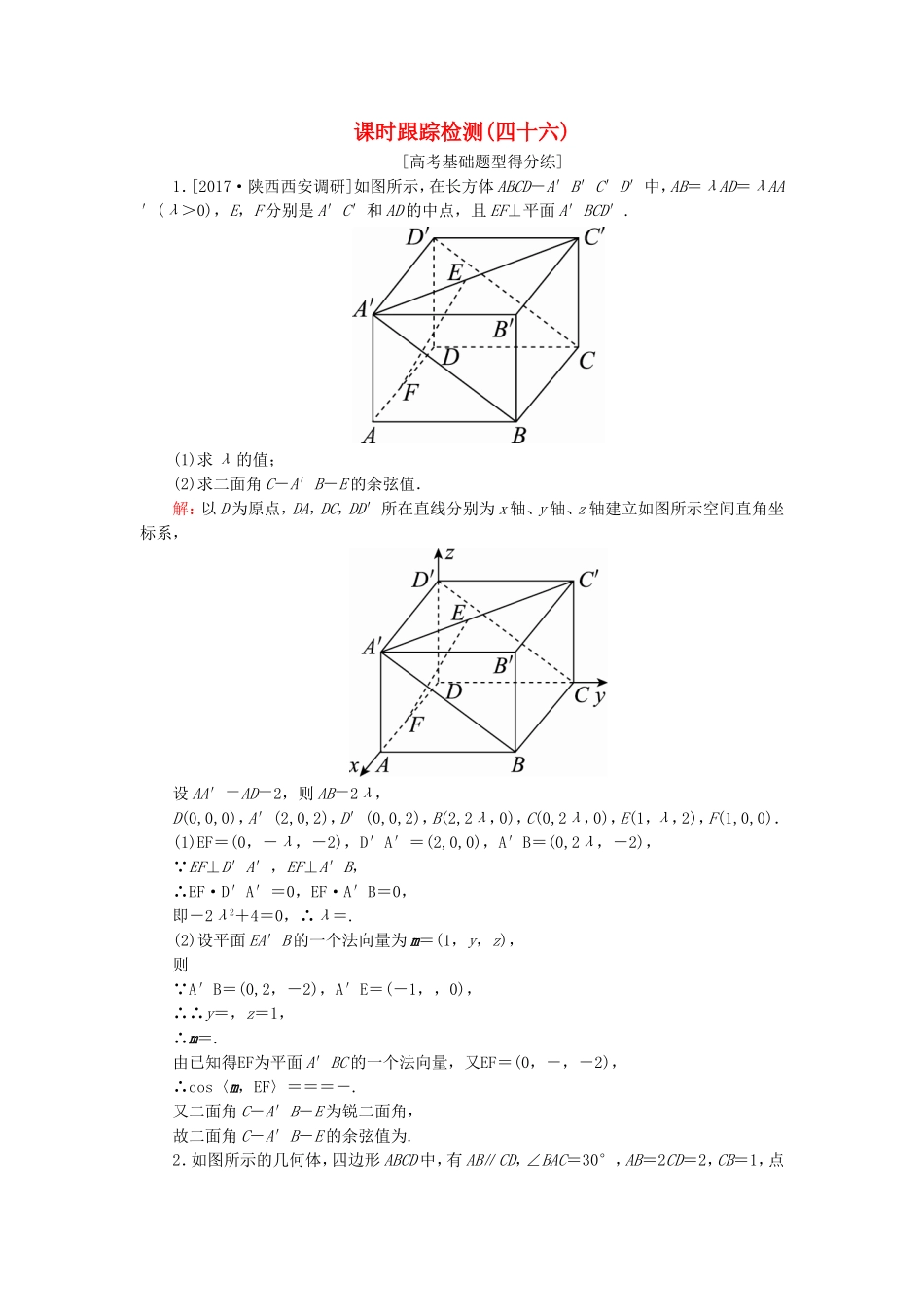
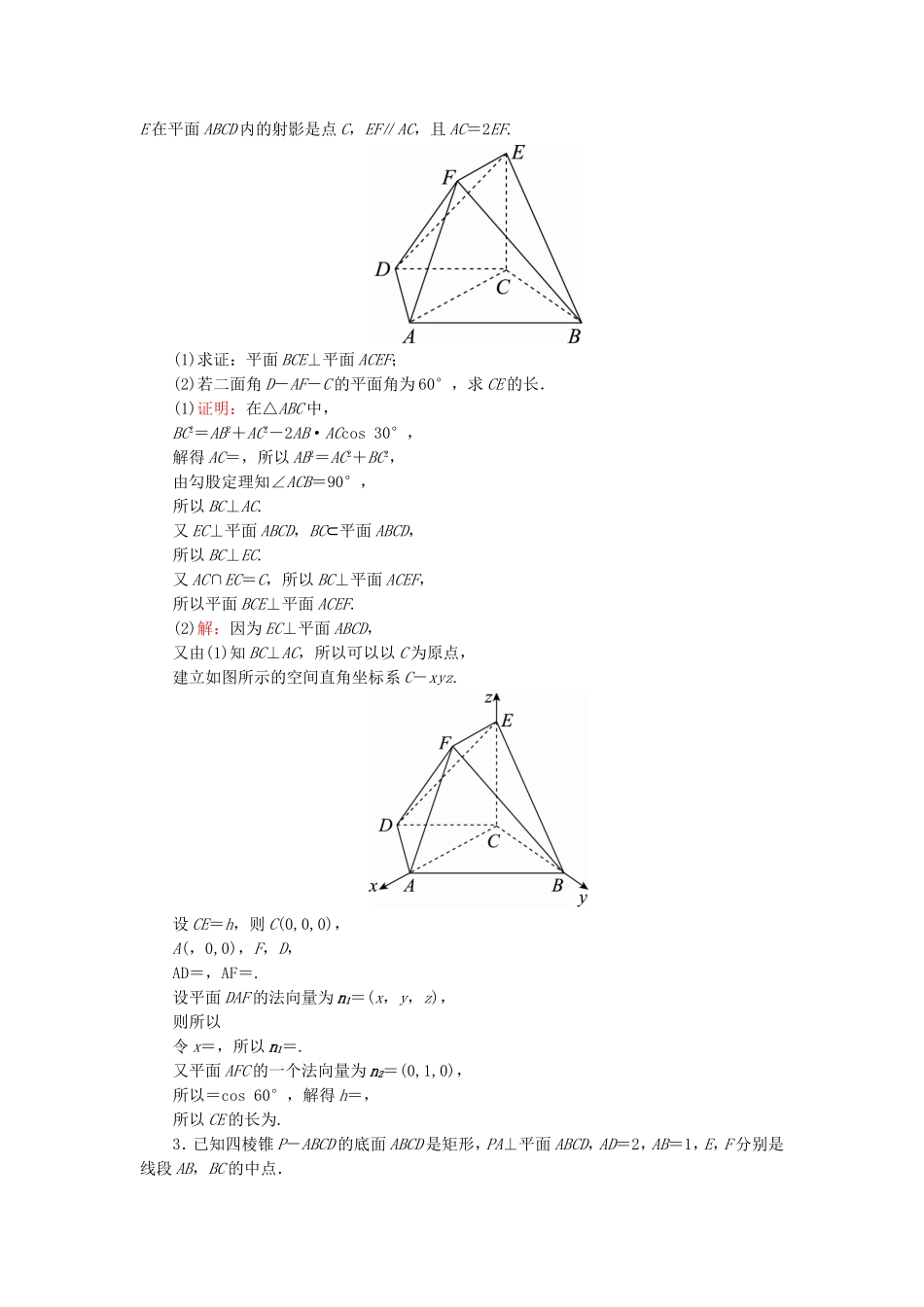
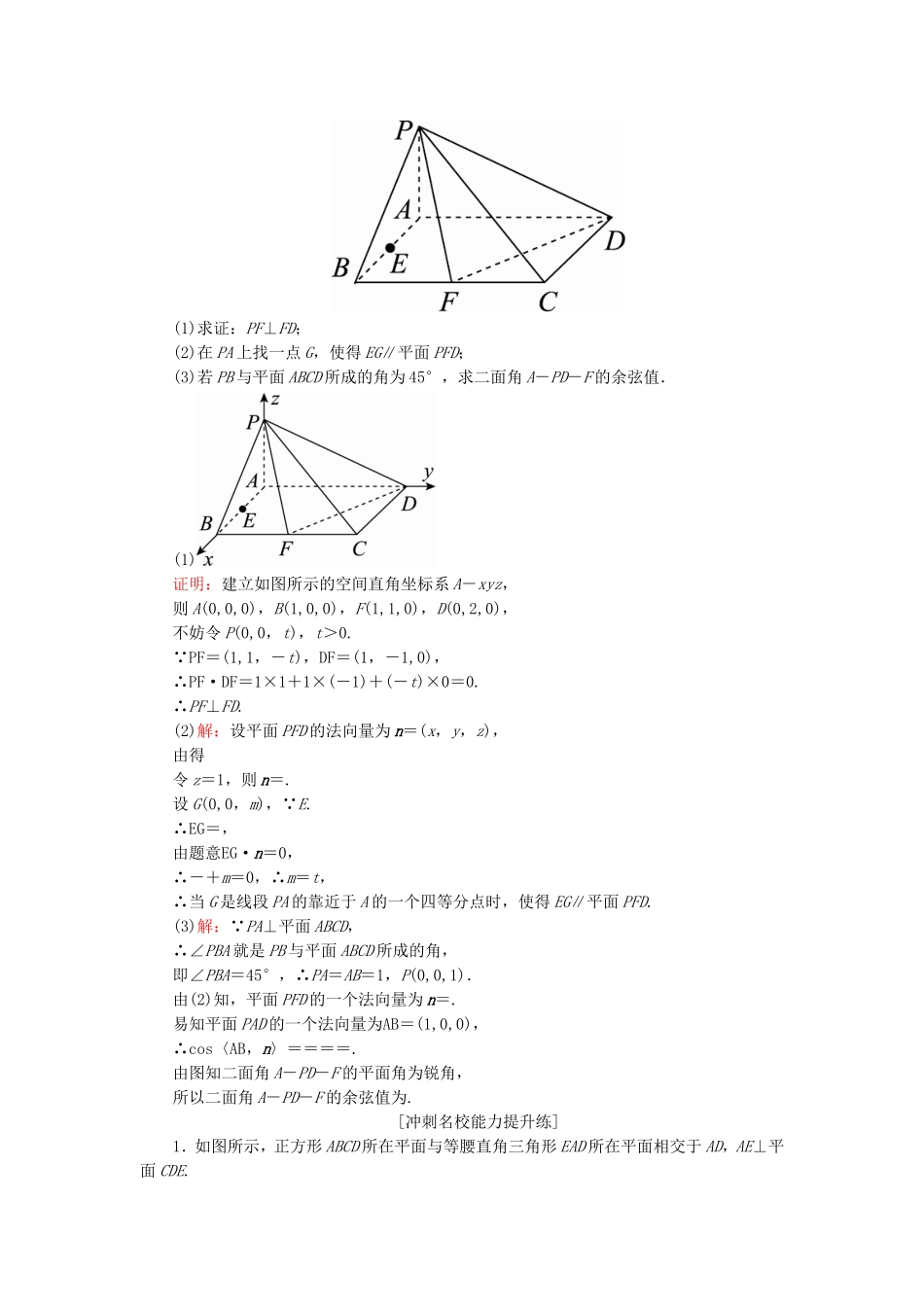
课时跟踪检测(四十六)[高考基础题型得分练]1.[2017·陕西西安调研]如图所示,在长方体ABCD-A′B′C′D′中,AB=λAD=λAA′(λ>0),E,F分别是A′C′和AD的中点,且EF⊥平面A′BCD′.(1)求λ的值;(2)求二面角C-A′B-E的余弦值.解:以D为原点,DA,DC,DD′所在直线分别为x轴、y轴、z轴建立如图所示空间直角坐标系,设AA′=AD=2,则AB=2λ,D(0,0,0),A′(2,0,2),D′(0,0,2),B(2,2λ,0),C(0,2λ,0),E(1,λ,2),F(1,0,0).(1)EF=(0,-λ,-2),D′A′=(2,0,0),A′B=(0,2λ,-2), EF⊥D′A′,EF⊥A′B,∴EF·D′A′=0,EF·A′B=0,即-2λ2+4=0,∴λ=.(2)设平面EA′B的一个法向量为m=(1,y,z),则 A′B=(0,2,-2),A′E=(-1,,0),∴∴y=,z=1,∴m=.由已知得EF为平面A′BC的一个法向量,又EF=(0,-,-2),∴cos〈m,EF〉===-.又二面角C-A′B-E为锐二面角,故二面角C-A′B-E的余弦值为.2.如图所示的几何体,四边形ABCD中,有AB∥CD,∠BAC=30°,AB=2CD=2,CB=1,点E在平面ABCD内的射影是点C,EF∥AC,且AC=2EF.(1)求证:平面BCE⊥平面ACEF;(2)若二面角D-AF-C的平面角为60°,求CE的长.(1)证明:在△ABC中,BC2=AB2+AC2-2AB·ACcos30°,解得AC=,所以AB2=AC2+BC2,由勾股定理知∠ACB=90°,所以BC⊥AC.又EC⊥平面ABCD,BC⊂平面ABCD,所以BC⊥EC.又AC∩EC=C,所以BC⊥平面ACEF,所以平面BCE⊥平面ACEF.(2)解:因为EC⊥平面ABCD,又由(1)知BC⊥AC,所以可以以C为原点,建立如图所示的空间直角坐标系C-xyz.设CE=h,则C(0,0,0),A(,0,0),F,D,AD=,AF=.设平面DAF的法向量为n1=(x,y,z),则所以令x=,所以n1=.又平面AFC的一个法向量为n2=(0,1,0),所以=cos60°,解得h=,所以CE的长为.3.已知四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,E,F分别是线段AB,BC的中点.(1)求证:PF⊥FD;(2)在PA上找一点G,使得EG∥平面PFD;(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的余弦值.(1)证明:建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(1,0,0),F(1,1,0),D(0,2,0),不妨令P(0,0,t),t>0. PF=(1,1,-t),DF=(1,-1,0),∴PF·DF=1×1+1×(-1)+(-t)×0=0.∴PF⊥FD.(2)解:设平面PFD的法向量为n=(x,y,z),由得令z=1,则n=.设G(0,0,m), E.∴EG=,由题意EG·n=0,∴-+m=0,∴m=t,∴当G是线段PA的靠近于A的一个四等分点时,使得EG∥平面PFD.(3)解: PA⊥平面ABCD,∴∠PBA就是PB与平面ABCD所成的角,即∠PBA=45°,∴PA=AB=1,P(0,0,1).由(2)知,平面PFD的一个法向量为n=.易知平面PAD的一个法向量为AB=(1,0,0),∴cos〈AB,n〉====.由图知二面角A-PD-F的平面角为锐角,所以二面角A-PD-F的余弦值为.[冲刺名校能力提升练]1.如图所示,正方形ABCD所在平面与等腰直角三角形EAD所在平面相交于AD,AE⊥平面CDE.(1)求证:AB⊥平面ADE;(2)在线段BE上存在点M,使得直线AM与平面EAD所成角的正弦值为,试确定点M的位置.(1)证明: AE⊥平面CDE,CD⊂平面CDE,∴AE⊥CD.在正方形ABCD中,CD⊥AD, AD∩AE=A,∴CD⊥平面ADE. AB∥CD,∴AB⊥平面ADE.(2)解:由(1)知,AB⊥平面ADE,又AB⊂平面ABCD,则平面EAD⊥平面ABCD,取AD的中点O,连接EO, EA=ED,∴EO⊥AD,又平面EAD∩平面ABCD=AD,EO⊂平面EAD,∴EO⊥平面ABCD,建立如图所示的空间直角坐标系,设AB=2,则A(1,0,0),B(1,2,0),E(0,0,1),设M(x,y,z),∴BM=(x-1,y-2,z),BE=(-1,-2,1), B,M,E三点共线,∴BM=λBE,∴M(1-λ,2-2λ,λ),∴AM=(-λ,2-2λ,λ),设AM与平面AED所成的角为θ, 平面AED的一个法向量为n=(0,1,0),∴sinθ=|cos〈AM,n〉|==,解得λ=.故点M为BE的中点.2.在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.(1)求证:AB⊥CD;(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.(1)证明: 平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AB⊂平面ABD,AB⊥BD,...