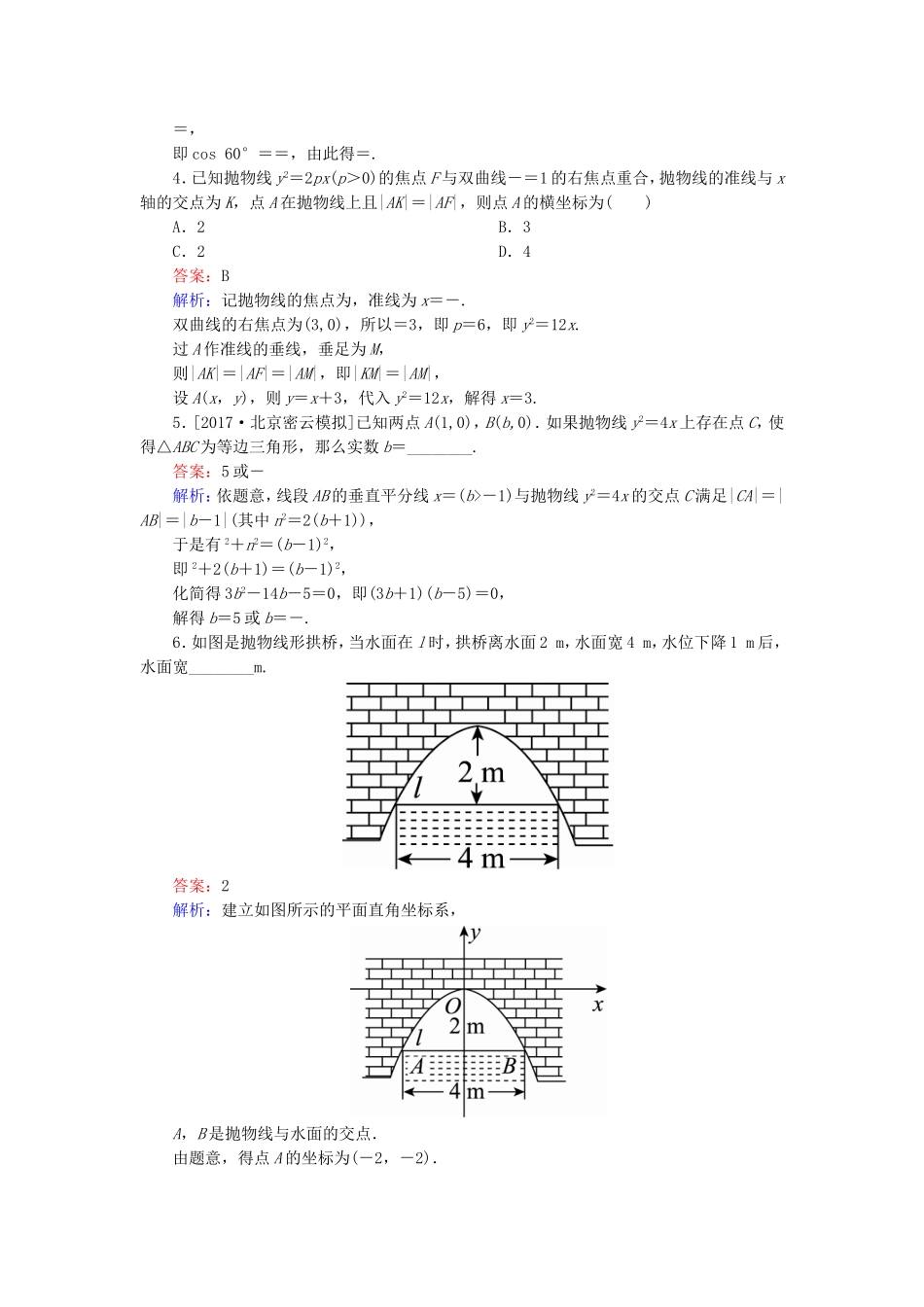
课时跟踪检测(五十三)[高考基础题型得分练]1.已知抛物线C:y2=x的焦点为F,A(x0,y0)是C上一点,|AF|=x0,则x0=()A.4B.2C.1D.8答案:C解析:由y2=x,得2p=1,即p=,因此焦点F,准线方程为l:x=-.设点A到准线的距离为d,由抛物线的定义可知d=|AF|,从而x0+=x0,解得x0=1,故选C.2.[2017·山西运城期末]已知抛物线x2=ay与直线y=2x-2相交于M,N两点,若MN中点的横坐标为3,则此抛物线方程为()A.x2=yB.x2=6yC.x2=-3yD.x2=3y答案:D解析:设点M(x1,y1),N(x2,y2).由消去y,得x2-2ax+2a=0,所以==3,即a=3,因此所求的抛物线方程是x2=3y.3.[2017·吉林长春一模]过抛物线y2=2px(p>0)的焦点F且倾斜角为120°的直线l与抛物线在第一、四象限分别交于A,B两点,则=()A.B.C.D.答案:A解析:记抛物线y2=2px的准线为l′,如图,作AA1⊥l′,BB1⊥l′,AC⊥BB1,垂足分别是A1,B1,C,则有cos∠ABB1===,即cos60°==,由此得=.4.已知抛物线y2=2px(p>0)的焦点F与双曲线-=1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|=|AF|,则点A的横坐标为()A.2B.3C.2D.4答案:B解析:记抛物线的焦点为,准线为x=-.双曲线的右焦点为(3,0),所以=3,即p=6,即y2=12x.过A作准线的垂线,垂足为M,则|AK|=|AF|=|AM|,即|KM|=|AM|,设A(x,y),则y=x+3,代入y2=12x,解得x=3.5.[2017·北京密云模拟]已知两点A(1,0),B(b,0).如果抛物线y2=4x上存在点C,使得△ABC为等边三角形,那么实数b=________.答案:5或-解析:依题意,线段AB的垂直平分线x=(b>-1)与抛物线y2=4x的交点C满足|CA|=|AB|=|b-1|(其中n2=2(b+1)),于是有2+n2=(b-1)2,即2+2(b+1)=(b-1)2,化简得3b2-14b-5=0,即(3b+1)(b-5)=0,解得b=5或b=-.6.如图是抛物线形拱桥,当水面在l时,拱桥离水面2m,水面宽4m,水位下降1m后,水面宽________m.答案:2解析:建立如图所示的平面直角坐标系,A,B是抛物线与水面的交点.由题意,得点A的坐标为(-2,-2).设抛物线的方程为x2=ay,把A的坐标代入,得a=-2,即抛物线的方程为x2=-2y.当水位下降1(单位:m)时,水面的纵坐标为-3,把y=-3代入抛物线的方程,得x=±.∴水位下降1m后,水面宽为2m.7.已知点M(-3,2)是坐标平面内一定点,若抛物线y2=2x的焦点为F,点Q是该抛物线上的一动点,则|MQ|-|QF|的最小值是________.答案:解析:抛物线的准线方程为x=-,当MQ∥x轴时,|MQ|-|QF|取得最小值,此时点Q的纵坐标y=2,代入抛物线方程y2=2x得Q的横坐标x=2,则|MQ|-|QF|=|2+3|-=.8.已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.(1)求曲线C的方程;(2)是否存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有FA·FB<0?若存在,求出m的取值范围;若不存在,请说明理由.解:(1)设P(x,y)是曲线C上任意一点,那么点P(x,y)满足-x=1(x>0).化简得y2=4x(x>0).(2)设过点M(m,0)(m>0)的直线l与曲线C的交点为A(x1,y1),B(x2,y2).设l的方程为x=ty+m,由得y2-4ty-4m=0,Δ=16(t2+m)>0,于是①又FA=(x1-1,y1),FB=(x2-1,y2),FA·FB<0.(x1-1)(x2-1)+y1y2=x1x2-(x1+x2)+1+y1y2<0.②又x=,于是不等式②等价于·+y1y2-+1<0,即+y1y2-[(y1+y2)2-2y1y2]+1<0.③由①式,不等式③等价于m2-6m+1<4t2.④对任意实数t,4t2的最小值为0,所以不等式④对于一切t成立等价于m2-6m+1<0,即3-2<m<3+2.由此可知,存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有FA·FB<0,且m的取值范围是(3-2,3+2).[冲刺名校能力提升练]1.已知抛物线x2=4y上一点A的纵坐标为4,则点A到抛物线焦点的距离为()A.B.4C.D.5答案:D解析:由题意知,抛物线的准线方程为y=-1,所以由抛物线的定义知,点A到抛物线焦点的距离为5.2.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若FP=4FQ,则|QF|=()A.B.C.3D.2答案:C解析:过点Q作QQ′⊥l交l于点Q′,...