反比例函数经典题型VIP免费

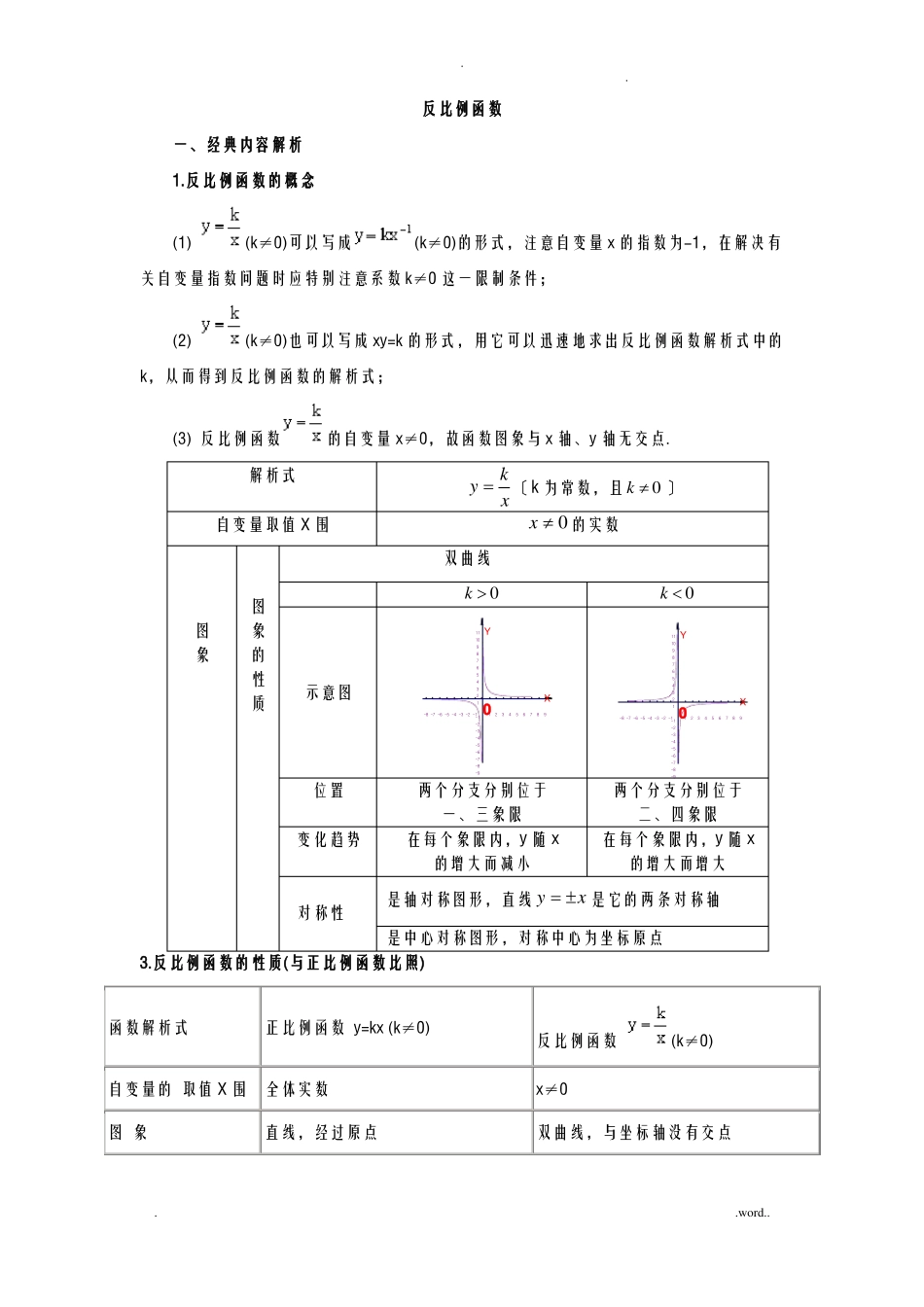
..反比例函数一、经典内容解析1.反比例函数的概念(1)(k≠0)可以写成(k≠0)的形式，注意自变量x的指数为-1，在解决有关自变量指数问题时应特别注意系数k≠0这一限制条件；(2)(k≠0)也可以写成xy=k的形式，用它可以迅速地求出反比例函数解析式中的k，从而得到反比例函数的解析式；(3)反比例函数解析式的自变量x≠0，故函数图象与x轴、y轴无交点.y自变量取值X围图象图象的性质示意图双曲线k〔k为常数，且k0〕xx0的实数k01110987654321-8-7-6-5-4-3-2-101-1-2-3-42345678k011109876543YYX921-8-7-6-5-4-3-2-101-1-2-3-4-5-6-7-8-92345678X9位置变化趋势对称性-5-6-7-8-9两个分支分别位于一、三象限在每个象限内，y随x的增大而减小两个分支分别位于二、四象限在每个象限内，y随x的增大而增大是轴对称图形，直线yx是它的两条对称轴是中心对称图形，对称中心为坐标原点3.反比例函数的性质(与正比例函数比照)函数解析式正比例函数y=kx(k≠0)反比例函数x≠0(k≠0)自变量的取值X围全体实数图象直线，经过原点双曲线，与坐标轴没有交点..word....图象位置(性质)当k＞0时，图象经过一、三象限；当k＜0时，图象经过二、四象限.当k＞0时，图象的两支分别位于一、三象限；当k＜0时，图象的两支分别位于二、四象限.性质(1)当k＞0时，在每个象限内y随x的(1)当k＞0时，y随x的增大而增大；增大而减小；当k＜0时，在每个象限当k＜0时，y随x的增大而减小.(2)越大，图象越靠近y轴.注：内y随x的增大而增大.(2)越大，图象的弯曲度越小，曲线越平直.(1)双曲线的两个分支是断开的，研究反比例函数的增减性时，要将两个分支分别讨论，不能一概而论.(2)正比例函数当当与反比例函数时，两图象没有交点；，时，两图象必有两个交点，且这两个交点关于原点成中心对称.(3)反比例函数与一次函数的联系.4.反比例函数中比例系数k的几何意义(1)过双曲线(k≠0)上任意一点作x轴、y轴的垂线，所得矩形的面积为.(2)过双曲线(k≠0)上任意一点作一坐标轴的垂线，连接该点和原点，所得三角形..word....的面积为1.反比例函数定义二、典型例题分析【例1】如果函数ykx2k值是多少？2k2的图像是双曲线，且在第二，四象限内，那么k的21.反比例函数y的图像位于〔〕xA．第一、二象限B．第一、三象限C．第二、三象限D．第二、四象限62.假设双曲线y＝－经过点A〔m，－2m〕，那么m的值为〔〕xA.3B.3C.±3D.±33.某反比例函数的图象经过点〔m，n〕，那么它一定也经过点〔〕A.〔m，－n〕B.〔n，m〕C.〔－m，n〕D.〔︱m︱，︱n︱〕4．〔2007XX〕在△ABC的三个顶点A(2，3)，B(4，5)，C(3，2)中，可能在反比例函数yk(k0)的图象上的点是．x5.假设点P〔4，m〕关于y轴对称的点在反比例函y=〔x≠0〕的图象上，那么m的值是2.反比例函数的表示【例2】yy1y2，y1与x成正比例，y2与x2成反比例，且x2时和x3时，y的值都是19，求y与x间的函数解析式1.假设y与x成反比例，x与z成正比例，那么y是z的〔〕A、正比例函数B、反比例函数C、一次函数D、不能确定2．y与(x2)成反比例关系，且当x1时，y4，那么y关于x的函数解析式为..word....3．y1与x成正比例〔比例系数为k1〕，y2与x成反比例〔比例系数为k2〕，假设函数yy1y2的图象经过点〔1，2〕，〔2，1〕，那么8k15k2．23.反比例函数的增减性问题【例.3】在反比例函数y1的图像上有三点x1，y1，xx2，y2，x3，y3。假设x1x20x3那么以下各式正确的选项是〔〕A．y3y1y2B．y3y2y1C．y1y2y3D．y1y3y21．在反比例函数图象上有两点A(，)，B()，当时，有，那么m的取值X围是().A．m＜0B．m＞0C．m＜0.5D．m＞0.52：反比例函数3：假设反比例函数，那么，上，有三点A(，，)，B(，)，C(，)，且的图象上两点A(，)，B(，)，当时，有，那么m的取值X围是_________.的大小关系是________.4.设有反比例函数yk1，假设x10x2(x1,y1)、(x2,y2)为其图象上的两点，x时，y1y2，那么k的取值X围是___________4.反比例函数与图象的面积问题.(1)求函数解析式1．如图，P是反比例函数图象在第二象限上的一点，且矩形PEOF的面积为3.求这个反...